ДВУСТОРОННИЕ ОЦЕНКИ ИНТЕНСИВНОСТЕЙ ОТКАЗОВ СИСТЕМ С ОБСЛУЖИВАНИЕМ БЕЗ ОЖИДАНИЯ И ВОЗВРАЩЕНИЕМ ВОССТАНОВЛЕННЫХ ЭЛЕМЕНТОВ В СИСТЕМЫ С МИНИМАЛЬНЫМ РЕЗЕРВОМ

Рассмотрим комплекс, в котором работают однотипных восстанавливаемых систем. С течением времени в каждой восстанавливаемой системе может возникнуть требование на обслуживание элемента из этой системы. Поток таких требований из каждой системы является пуассоновским с параметром . В момент отказа элемента в одной из систем возникает требование на его обслуживание, которое немедленно поступает в ремонтный орган (РО) с неограниченным числом обслуживающих приборов, где без ожидания осуществляется восстановление элемента. Восстановленный элемент возвращается в ту систему, в которой резерв минимальный, а требование на его обслуживание немедленно покидает РО.

Длины требований (различных элементов или различных отказов одного и того же элемента) есть независимые положительные случайные величины. Обозначим - функцию распределения длины требования по обслуживанию отказавшего элемента. Ее первый момент обозначим , . Пусть - суммарная нагрузка на РО всех систем комплекса, . Состояние комплекса описывает случайный процесс

где - число неисправных элементов в -й системе. Система неисправна, если число неисправных элементов в ней больше, чем . Восстановление системы происходит, если число неисправных элементов в ней меняется с на . Пусть - множество исправных, а - множество неисправных состояний й системы.

Пусть - интенсивность отказа й системы комплекса.

Теорема 1.

Пусть и . Тогда

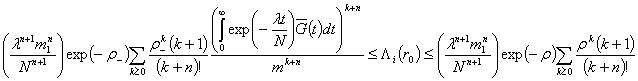
Так, для , и правило возвращения элемента в систему с минимальным резервом в сравнении с возвращением элемента в ту систему, где он отказал, позволяет снизить интенсивности отказа систем в раз!

Литература.

1. Макаричев А.В. Оптимальное возвращение элементов в комплекс возобновляемых систем с горячим резервом. Электронное моделирование, 1993, № 1, 74-77.

2. Макаричев А.В. Оптимальное распределение элементов в комплексе

восстанавливаемых систем с холодным резервом. Теория

вероятностей и ее применения. 1995, том 40, вып. 1, с. 84-95.

3. Макаричев А.В. Оптимальное восстановление резерва элементов в комплексах возобновляемых систем с неограниченным числом элементов, стр. 18 – 25. Материали за 8-а международна научна практична конференция, «Научният потенциал на света», - 2012. Том 16. Математика. Съвременни технологии на иформации. София. «Бял ГРАД-БГ» ООД – 80 стр.