К.т.н. Заика И.В., д.т.н., Ромм Я.Е.
Таганрогский
государственный педагогический институт им. А.П. Чехова, Россия
Схема
автоматической идентификация решений систем уравнений на основе сортировки
Для идентификации нулей линейных и
нелинейных алгебраических систем уравнений, а так же трансцендентных систем
уравнений применяется схема сортировки с взаимно однозначным соответствием
входных и выходных индексов сортируемых элементов. К программе сортировки [1] подсоединяется
условный оператор, локализующий все минимумы среди элементов входной
последовательности. Фиксируется любое 
меньшее половины минимального
расстояния между минимумами. Условие локализации всех минимальных в 
-окрестности значений дискретизированной функции одной
переменной на равномерной сетке с шагом 
примет вид [1]: 
. Здесь 
– элемент массива
входных индексов, располагаемого в порядке отсортированных по неубыванию значений
функции, образующих одномерный массив. Условие означает, что в 
-окрестности узла с индексом 
нет индекса входного
элемента, который бы превосходил элемент с индексом 
. Максимумы локализуются аналогично [1]. Нули функции идентифицируются
как достаточно малые минимумы модулей значений на равномерной сетке. С
использованием плоской равномерной прямоугольной сетки схема распространяется на
идентификацию экстремумов и нулей функций двух переменных [2]. Дискретизированные
значения функции интерпретируются как двумерные массивы. Данная схема следующим
образом применяется к безусловной численной
локализации нулей систем однородных уравнений. Пусть исходная система
нелинейных уравнений преобразована к виду однородной системы
(1)
с действительными левыми частями (как последует из
построения, метод распространяется на случай комплексной левой части).
Совокупность аргументов 
можно рассматривать
как n-мерный вектор с действительными компонентами.
Аналогично совокупность функций 
представляет собой также n-мерный вектор с действительными компонентами. Пусть
требуется найти все решения системы (1) в многомерном параллелепипеде, входящем
в область ее определения. Строится равномерная сетка, в узлах которой значения
канонической нормы вектор-функции из левой части (1) (для определенности норма
– сумма модулей компонент) принимаются за элементы массива:
, 
. (2)
На вход алгоритма идентификации минимумов функции n переменных
подается массив (2), после чего идентифицируются все нули системы (1) как
минимумы нормы левой части. При этом первоначально идентифицируются все
минимумы, затем среди них выбираются те, которые близки к нулю с априори
заданной точностью : 
.
Пример. Приближенное решение системы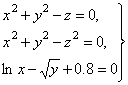 
в параллелепипеде 
, 
, 
вычисляется по
программе (Delphi):
Program UravnNelin;
{$APPTYPE CONSOLE}
Uses
SysUtils;
label 21,22,23;
const eps0=0.1; h=eps0/23; x00=0.1; x11=1;
y00=0; y11=1; z00=0; z11=1;
n00=trunc(4/h); nn=n00+round(n00/2)+1;
type vect1=array [1..2*nn+nn] of extended;
vect2=array [1..2*nn+nn] of longint;
var
i,j,k,k1,r,rx,ry,rz,nn0,kx,ky,kz : longint;
c,a1,az: vect1; e, ex, ey,ez: vect2;
x,x0,x1,xk,minx,minz: extended;
y,y0,y1,yk,z0,z1,z,zk: extended;
function f1 (x,y,z:extended):extended;
begin
f1:= x*x+y*y-z ; end;
function f2 (x,y,z:extended):extended;
begin f2:= x*x+y*y-z*z; end;
function f3 (x,y,z:extended):extended;
begin f3:= ln(x)-sqrt(y)+0.8; end;
function func (x,y,z:extended):extended;
var p: extended; i1: integer;
begin func:= abs(f1(x,y,z))+abs(f2(x,y,z))+abs(f3(x,y,z));
end;
procedure minyz (var x,y,z,minx:extended);
begin minx:=func(x,y,z);
for i:=1 to trunc((y11-y00)/h) do
for j:=1 to trunc((z11-z00)/h) do
begin y:=y0+i*h; z:=z0+j*h;
IF minx > func(x,y,z) then minx:=func(x,y,z)
end end;
procedure minyy (var x,y,z,minz:extended);
begin minz:=func(x,y,z); for i:=1 to
trunc((y11-y00)/h) do
begin y:=y0+i*h; IF minz > func(x,y,z) then
minz:=func(x,y,z) end end;
{Описание
процедуры
сортировки
sort}
procedure sort(var nn0:longint; var с: vect1; var e: vect2);
var
i,j,k: longint;
begin
for j:=1 to nn0 do begin k:= 0;
for i:=1 to j
do if с[j]>=с[i]
then k:=k+1;
for i:=j+1 to nn0 do if с[j]>с[i]
then k:=k+1;
e[k]:=j;
end;
end;
BEGIN x0:=x00; x1:=x11; y0:=y00; y1:=y11;z0:=z00; z1:=z11; nn0:=n00;
for rx:=1 to nn0 do begin x:=x0+rx*h; minyz
(x,y,z,minx); a1[rx]:=minx; end;
sort( nn0, a1, ex); kx:=1; while kx<= nn0 do
begin
for rx := 1 to kx-1 do IF abs( ex[kx]-ex[kx-rx]
) <= eps0/h then goto 21;
xk:= x0+ex[kx]*h; for rz:=1 to nn0 do begin
z:=z0+rz*h; x:=xk; minyy (x,y,z,minz);
az[rz]:=minz; end;
sort( nn0, az, ez); kz:=1; while kz<= nn0 do
begin
for rz := 1 to kz-1 do IF abs(ez[kz]-ez[kz-rz])
<=eps0/h then goto 22;
zk:= z0+ez[kz]*h;
for ry:=1 to nn0 do begin y:=y0+ry*h;
a1[ry]:=func(xk,y,zk) end;
sort( nn0, a1, ey); ky:=1; while ky<= nn0 do
begin
for ry := 1 to ky-1 do IF abs(ey[ky]-ey[ky-ry])
<=eps0/h then goto 23;
yk:= y0+ey[ky]*h; writeln (' ', xk:30:4,' '); writeln (' ',
yk:30:4,' ');
writeln ('
', zk:30:4,' ',
f1(xk,yk,zk):2:4,'
',f2(xk,yk,zk):2:4,'
',f3(xk,yk,zk):2:4);
writeln;
23: ky:=ky+1; end;
22: kz:=kz+1; end;
21: kx:=kx+1; end; writeln('end'); readln; end.
Для данного
примера получатся значения:
|
Значения
аргументов |
Значения
компонент |
||
|
X |
y |
z |
|
|
0.8870 |
0.4609 |
1.0000 |
f1= -0.0009 f2= -0.0009 f3= 0.0012 |
Для
нелинейных систем с неединственным решением схема позволяет программно
локализовать все минимумы нормы (2) и среди них наиболее близкие к нулю, их
локализация в окрестности наперед заданного радиуса означает приближение к
решению по норме с точностью до значения радиуса. Например, для системы
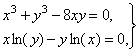
которая
имеет три решения, предложенная схема дает семь значений минимумов нормы, из
них три наименьшие, достаточно близкие к нулю (выделены подчеркиванием),
приближают искомые решения:
|
Значения аргументов |
Значения
компонент f1 f2 |
|
|
x |
y |
|
|
1.94007 |
3.67910 |
-0.0000000000 0.0890364151 |
|
2.07596 |
3.77313 |
-0.0000000000
0.0006942907 |
|
2.49393 |
4.01045 |
-0.0000000000 -0.2011612746 |
|
3.67927 |
1.94030 |
0.0000000000 -0.0888810927 |
|
3.77324 |
2.07612 |
0.0000000000
-0.0005957791 |
|
4.01049 |
2.49403 |
0.0000000000
0.2011954085 |
|
4.00000 |
4.00000 |
-0.0000000000 0.0000000000 |
Схема без изменения
применима для приближенных решений систем линейных и нелинейных алгебраических,
а также трансцендентных уравнений [2], по способу компьютеризации отличаясь от
аналогов [4, 5]. На вход метода поступают значения функции, которые с учетом
общности ограничений могут вырабатываться в результате решения некоторой другой
задачи в реальном времени. Существенным ограничением при этом является
требование достаточной малости шага дискретизации. Отличительным качеством, как
и в двумерном случае, остается отсутствие начальных приближений, а также
области локализации экстремумов, используемых в математических методах [5,6].
Численный эксперимент показывает применимость схемы в случае вектор-функций из
левой части (1) со сложным рельефом [2], включая разрывы первого рода.
Литература:
1.
Ромм Я.Е. Локализация и
устойчивое вычисление нулей многочлена на основе сортировки. I // Кибернетика и
системный анализ. – 2007. – № 1. – С. 165 – 182.
2.
Заика И.В. Разработка и
исследование схем оптимизации на основе алгоритмов сортировки с приложением к
идентификации экстремумов решений дифференциальных уравнений. – Таганрог: ТРТУ,
2007, автореферат диссертации на соискание ученой степени канд. техн. наук.
3.
Ромм Я.Е. Параллельная
сортировка слиянием по матрицам сравнений. II // Кибернетика и системный анализ. – 1995. – № 4. –
С. 13 – 37.
4.
Березин И.С., Жидков
Н.П. Методы вычислений. Т.2. – М.: Физматгиз, 1962. – 640 с.
5.
Демидович Б.П.,
Марон И.А. Основы вычислительной математики. – М.: Физматгиз, 1963. –
660 с.
6.
Васильев Ф.П. Численные
методы решения экстремальных задач. – М.: Наука, 1988. – 552с.