Сметанкин В

К. т. н. Сметанкина Н.В., к. т. н. Сметанкин В.А., Сметанкин А.В.

Институт проблем машиностроения им. А.Н. Подгорного НАН Украины, Украина

Анализ напряженного состояния пластин на основе интегральных уравнений теории упругости

Собственные напряжения в элементах машиностроительных конструкций, обусловленные, например, технологическими причинами (литьём, сваркой, штамповкой и т. д.), существенно влияют на их прочностные свойства. Один из распространённых способов исследования собственных напряжений, состоит в том, что напряжения измеряются не в самом элементе конструкции, а в вырезанном из него образце (темплете) [1]. При этом напряжения в исходном элементе до вырезки темплета считаются равными напряжениям в темплете после его вырезки. После вырезки темплета происходит изменение напряжённого состояния и изменённые напряжения в темплете после его вырезки не будут равны исходным напряжениям в элементе. В связи с этим практический интерес представляет задача об определении исходных напряжений в элементе конструкции по измеренным напряжениям в вырезанном темплете. Данная статья посвящена восстановлению исходного напряжённого состояния в элементе конструкции по измеренным напряжениям в вырезанном темплете.

Очевидно, что после вырезки темплета напряжения на его поверхности становятся равными нулю. Такое же напряжённое состояние получается, если к границам темплета приложить напряжения, равные собственным напряжениям, но с обратным знаком. Таким образом, имеем

, (1)

где – напряжения в вырезанном темплете; s – собственные напряжения в детали; – напряжения в темплете, обусловленные приложением к его границам нагрузок, равных собственным напряжениям с обратным знаком.

В качестве модели элемента конструкции с собственными напряжениями рассмотрим плоскую пластинку с прямолинейным сварным швом. Обычно вырезанный темплет имеет форму прямоугольника, расположенного симметрично сварному шву. Измерение напряжений в вырезанном темплете производится методом полосок [1], который состоит в том, что вырезанный темплет разрезается на “полоски”, расположенные параллельно сварному шву. Напряжения в вырезанном темплете определяются в соответствии с законом Гука

где – напряжение в i-ой полоске, E – модуль упругости материала детали, – длины полосок до и после вырезки темплета соответственно.

Систему координат расположим в срединной плоскости пластины с началом координат, совпадающим с центром темплета, и осью , направленной вдоль шва. В связи с тем, что напряжения локализуются в окрестности сварного шва, удлинение темплета в направлении оси Ox не приведёт к существенному изменению напряжённого состояния в наиболее напряжённой области – в районе сварного шва. Поэтому будем считать темплет бесконечно длинным в направлении оси Ox, что даёт возможность значительно упростить вычисления.

Измерение напряжений в темплете “методом полосок” даёт, очевидно, среднее напряжение в каждой полоске, определяемое с помощью соотношения

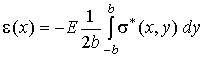, (2)

где – длина полоски; e – её относительная деформация. При этом ширина полоски считается достаточно малой.

Соотношение (1), с учётом вычисления усреднённых напряжений по длине полосок, можно записать в виде

, (3)

где черта означает усреднение по длине полосок.

Для определения используем решение Файлона [2, 3] плоской задачи теории упругости о напряжённом состоянии внутри полосок при заданном нормальном напряжении на её границах. Из решения этой задачи следует, что касательные напряжения внутри полоски являются нечётными функциями координаты y. Поэтому при усреднении по ширине полоски для касательных напряжений получим нуль. Нормальные напряжения на площадках, перпендикулярных к оси , быстро падают с увеличением координаты x. Таким образом, напряжённое состояние внутри вырезанного темплета, ещё не разрезанного на полоски, определяется соотношениями:

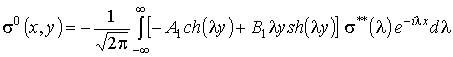, (4)

где

, , .

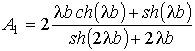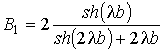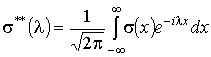Подставляя (2) в (1) и используя (4), запишем

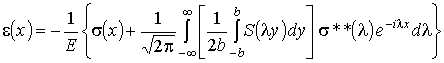, (5)

где

Вычислим интеграл 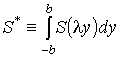. С учетом (4) и (5), получим

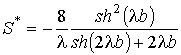Таким образом, выражение (5) для деформации полоски преобразуется к виду

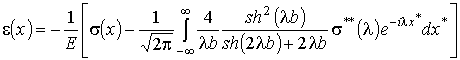. (6)

Это соотношение является уравнением Фредгольма второго рода [4] относительно неизвестной величины – исходного распределения напряжений в детали. Для решения этого уравнения выполним преобразование равенства (6), используя теорему Фурье [3]

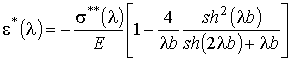, (7)

где – преобразование Фурье .

Из (7) находим

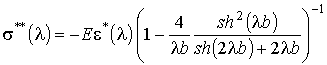Отсюда по теореме обращения получаем

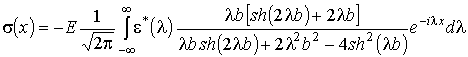. (8)

Используя теорему Фурье [5], запишем это соотношение в виде

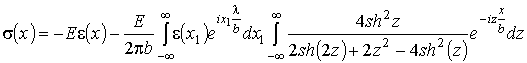. (9)

Как следует из разложения функции в ряд Тейлора по степеням z,

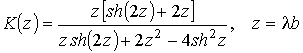, (10)

подынтегральная функция в (8) имеет полюс четвёртого порядка.

Обозначим знаменатель дроби в (9) как и запишем

Отсюда, используя разложение экспонент в ряд Тейлора, находим

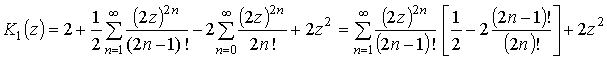Ограничиваясь первыми тремя членами суммы, получим . Следовательно, разложение функции (10) запишется как .

Преобразуем равенство (9) к следующему виду:

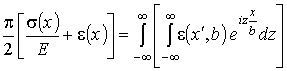. (11)

Отсюда следует, что при больших значениях b (, a – размер темплета в направлении оси ), правая часть равенства (16) будет малой величиной, так как при больших значениях b будет малой величиной

Представим правую часть (11) в виде суммы , где

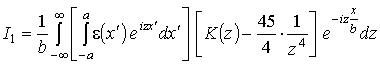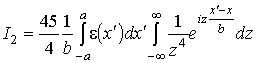. (12)

Внешний интеграл в выражении для сходится равномерно. Это следует из того, что при для на основании (10) имеем оценку , а при – . Таким образом, для вычисления могут быть использованы известные методы приближённого вычисления преобразования Фурье. Интегральное выражение (12), определяющее , непосредственно не может использоваться в численных расчётах, так как внутренний интеграл не сходится в классическом смысле и может рассматриваться как линейный функционал на пространстве K основных функций, требующий регуляризации, либо как преобразование Фурье обобщённой функции. Используем второй способ, то есть преобразование Фурье обобщённой функции.

В соответствии с общим методом [6] по аналогии с вычислением преобразования Фурье обобщённых функций и находим для внутреннего интеграла в (12) представление 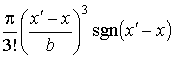, используя которое, получим

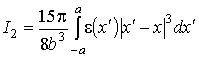Разбиваем промежуток интегрирования на малые отрезки, в пределах которых выражение имеет постоянный знак. При этом считаем функцию чётной, что согласуется с выбранной моделью и в большинстве случаев имеет место в реальных конструкциях. С учетом этих условий запишем

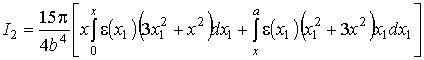В результате получаем выражение для исходного распределения собственных напряжений в пластине

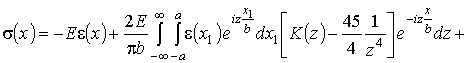
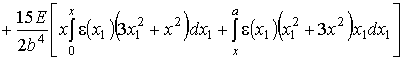Таким образом, получено соотношение, которое даёт возможность определить исходные напряжения в детали по измеренным деформациям полосок в вырезанном темплете.

Литература:

1. Патон Е.О. Избранные труды. – Т. 2. – К.: Изд.-во АН УССР, 1961. – 680 с.

2. Ляв А. Математическая теория упругости. – М.: ОНТИ, 1935. – 662 с.

3. Снеддон И. Преобразования Фурье.– Т. 1.– М.: Изд.-во иностр. лит.-ры, 1955.– 667 с.

4. Забрейко П.П. Интегральные уравнения.– М.: Наука, 1968.– 446 с.

5. Крылов В.И., Скобля Н.С. Методы приближенного преобразования Фурье и обращение преобразования Лапласа. – М.: Наука, 1974.– 223 с.

6. Гельфанд И.М., Шилов Г.Е. Обобщённые функции.– М.: Физматгиз, 1959.– 470 с.