Математика/4.Прикладная математика

Даулетбаева Ж.Д., старший преподаватель

Костанайский государственный университет, Казахстан

Гармоническая функция и ее приложение

Рассмотрим уравнение Лапласа на плоскости

(1)

и в пространстве

(2)

Функции U=U(x,y) на плоскости и U=U(x,y,z) в пространстве, имеющие непрерывные частные производные второго порядка и удовлетворяющие, соответственно, уравнению Лапласа (1) или (2) в некоторой области D, называются гармоническими в этой области.[1]

Простейшими примерами гармонических функций являются линейные функции: на плоскости и в пространстве. Особый интерес представляют решения уравнений Лапласа, обладающие сферической или цилиндрической (в случае двух независимых переменных – круговой) симметрией.

Решение , обладающее сферической симметрией, будет определяться из обыкновенного дифференциального уравнения

Это уравнение получится, если подставить искомую функцию в уравнение Лапласа (2), записанное в сферических координатах. Интегрируя это уравнение, находим где и - произвольные постоянные. Полагая , ,получим функцию которую часто называют фундаментальным решением уравнения Лапласа в пространстве. Функция является гармонической всюду в пространстве, кроме начала координат.

Аналогично, полагая и пользуясь уравнением Лапласа в цилиндрических и полярных координатах можно найти решения, обладающие цилиндрической или круговой симметрией:

где

Выбирая и , будем иметь функцию которую называют фундаментальным решением уравнения Лапласа на плоскости (в случае двух независимых переменных). Функция удовлетворяет уравнению Лапласа (1) всюду на плоскости, кроме начала координат, где она обращается в бесконечность. Фундаментальные решения уравнения Лапласа имеют, помимо большого значения в теории гармонических функций, важный физический смысл.

Рассмотрим в пространстве электрическое поле, образованное точечным зарядом величины , помещенным в начало координат. Тогда потенциал этого поля равен Аналогично, если рассмотреть поле, создаваемое заряженной прямой, то потенциал такого поля будет равен где - линейная плотность заряда (то есть заряд, рассчитанный на единицу длину).

А теперь приступим к изучению некоторых свойств гармонических функций.

Теорема о среднем. Пусть функция гармоническая в некотором круге радиуса с центром и непрерывная в соответствующем замкнутом круге . Тогда значение этой функции в центре круга равно ее среднему значению на окружности Г, ограничивающей данный круг [14], то есть 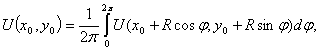(3)

При доказательстве этой теоремы применяется интегральная формула Пуассона для круга, которая будет доказана позже. Она имеет вид

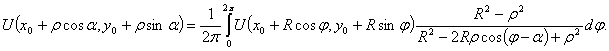
Если в этой формуле положить , то получится формула (3).

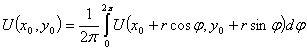Теорему о среднем можно представить и в другой форме. Для этого запишем формулу (3) для произвольного круга радиуса , где (4)

Умножив обе части равенства (4) на и проинтегрировав по в пределах от 0 до , получим: 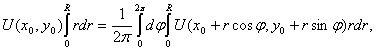или

где - круг радиуса . Разделив обе части полученного равенства на , получится (5)

В правой части формулы (5) записано среднее значение гармонической функции U(x,y) в круге радиуса R [1].

Имеет место и обратная теорема: если в некоторой области функция непрерывная и для каждой точки выполняется теорема о среднем в любом сколь угодно малом круге с центром в точке , то эта функция гармоническая в .

Литература:

1. Владимиров В.С. Уравнения математической физики. – М., Наука, 1967.

2. Михлин С.Г. Курс математической физики. - М., Наука, 1968.