Математика/4. Прикладная математика

Д.ф.м.-н. Бурова И.Г.

Санкт-Петербургский государственный университет, Россия

О построении численных методов решения задачи Коши на основе неполиномиальных интегро-дифференциальных сплайнов

Полиномиальные минимальные сплайны подробно изучены в работе [1]. В книге [2] рассмотрены полиномиальные интегро-дифференциальные сплайны. В статье [3] предложены неполиномиальные интегро-дифференциальные сплайны. В данной статье будут представлены неявные интерполяционные методы численного решения задачи Коши, полученные с помощью полиноми-альных и неполиномиальных интегро-дифференциальных сплайнов [3].

Вначале обсудим построение интегро-дифференциальных базисных сплайнов третьего порядка аппроксимации. Для удобства изложения рассматриваем равномерную сетку узлов.

Пусть - сетка упорядоченных узлов на промежутке [a,b], чебышевская система на . Предполагаем, что определитель Вронского, построенный по системе , отличен от 0 на промежутке . На промежутке функцию , , приближаем с помощью

Здесь , а базисные функции находим из соотношений

В [3] показано, что при где – однородное дифференциальное уравнение, имеющее фундаментальную систему решений Приведем два частных случая.

1) Пусть

Переходя к переменной получаем формулы

Нетрудно видеть, что при Графики базисных функций и представлены на рис.1:

251658240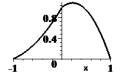251658240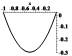

Рис.1. Графики базисных функций при h=1

Интегрируя базисные сплайны, получаем

2) Пусть теперь

Переходя к переменной получаем формулы

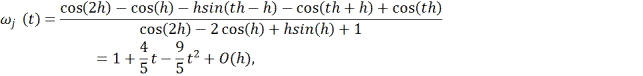
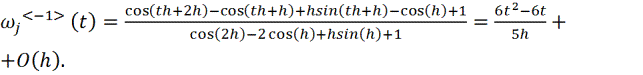
Интегрируя, получаем

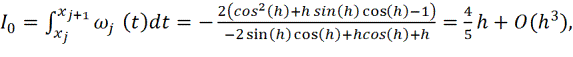
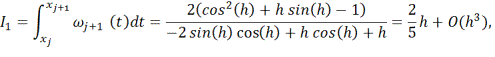
Последние три равенства связывают выражения для интегралов от полиномиальных и тригонометрических сплайнов. Аналогично строятся интегро-дифференциальные сплайны четвертого порядка. Далее покажем, как построить численный метод для решения задачи Коши

, ∈

Заменяя в формуле Ньютона-Лейбница

подынтегральное выражение на получаем

Поэтому, например, в полиномиальном случае имеем правило

причем для погрешности

имеем неравенство

Аналогично, применяя интегро-дифференциальные сплайны четвертого порядка, получаем метод

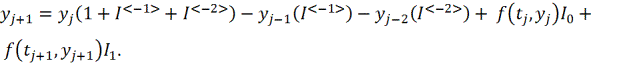
В полиномиальном случае имеем

с погрешностью, определяемой следующим соотношением при некотором

Для построения начала таблицы можно применять неявные интерполяционные методы, построенные на основе сплайнов ненулевой высоты [1, 3]. В случае равномерной сетки с шагом h и полиномиальных базисных функций

где

Для погрешности справедливо неравенство

Методы более высокого порядка для одного уравнения строим аналогично. Очевидно легко получить обобщение для решения систем уравнений..

Пример. Будем решать уравнение

Очевидно решение этой задачи

Строим приближенные решения с помощью предложенных методов при шаге сетки 0.1 на промежутке [0,100]. На рис.2 для метода третьего порядка представлены точное и приближенное решения.

251658240

Рис.2. Графики точного решения (y=sin(x) – сплошная линия) и

приближенного решения (точки)

Для всех представленных численных методов решения задачи Коши численные вычисления подтверждают теоретическую оценку погрешности.

Литература

1. Бурова И.Г., Демьянович Ю.К. Минимальные сплайны и их приложения. СПб. 2010. 364 c.

2. Киреев В.И., Пантелеев А.В. Численные методы в примерах и задачах. М. 2008. 480 c.

3. Бурова И.Г. О моделировании неполиномиальных интегро-дифференциальных приближений // Труды СПИИРАН. Вып. 4(19). 2010. с.176-202.