Математика/4. Прикладная математика
Асканбаева
Г.Б.
Костанайский государственный университет им. А.
Байтурсынова, Казахстан
Унитарные пространства
Пусть дано
комплексное линейное пространство ![]() . Говорят, что в
. Говорят, что в ![]() определена операция
скалярного умножения векторов, если любой паре векторов х и у из
определена операция
скалярного умножения векторов, если любой паре векторов х и у из ![]() поставлено в
соответствие комплексное число, называемое скалярным произведением векторов х и
у и обозначаемое символом
поставлено в
соответствие комплексное число, называемое скалярным произведением векторов х и
у и обозначаемое символом ![]() , и если для любых х,у,z из
, и если для любых х,у,z из ![]() и любого комплексного
числа α выполняются следующие аксиомы:
и любого комплексного
числа α выполняются следующие аксиомы:
1.
![]()
2.
![]()
3.
![]()
4.
![]() при
при ![]() и
и ![]() при
при ![]()
Определение: Комплексное n-мерное
линейное пространство, в котором определена операция скалярного умножения
векторов, называют n-мерным
унитарным пространством и обозначают через ![]() .
.
Из первой,
второй, третьей аксиом скалярного произведения следует
![]() (1)
(1)
![]() (2)
(2)
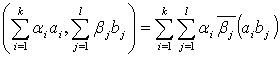 (3)
(3)
Если в унитарном пространстве ![]() фиксирован базис
фиксирован базис ![]() , то любые векторы х и у имеют в нем разложения
, то любые векторы х и у имеют в нем разложения
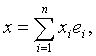
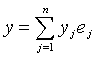 , то
, то 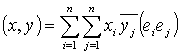
или в матричной записи
![]()
где положено ![]()
![]()
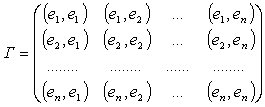 - матрица Грамма
- матрица Грамма
Поскольку ( еi,ej) =
(ej,ei),
матрица грамма удовлетворяет условию
![]() (4)
(4)
Звездочка означает транспонирование матрицы с
последующей заменой в ней элементов на комплексно сопряженные. [1]
Определение.
Матрицу ![]() называют сопряженной
к матрице
называют сопряженной
к матрице ![]() . если
. если ![]() , то матрицу А называют эрмитовой. Так, в силу условия (4),
матрица Грамма – эрмитова. Если матрица
, то матрицу А называют эрмитовой. Так, в силу условия (4),
матрица Грамма – эрмитова. Если матрица ![]() действительная,
то
действительная,
то ![]()
В
унитарном пространстве, как и в
евклидовом, длину вектора определяют формулой
![]() (5)
(5)
Понятие
угла между векторами в унитарном пространстве, как правило, не вводят.
Рассматривают лишь случай ортогональности векторов. При этом, как и в
евклидовом пространстве, ортогональными считают векторы х и у,
удовлетворяющие условия (х,у) = 0.
Формула скалярного
произведения принимает вид
![]() (6)
(6)
а для скалярного квадрата она превращается в формулу
![]() (7)
(7)
Эти формулы постоянно применяются при решении задач в
унитарном пространстве.
Определение: Квадратную матрицу ![]() , для которой сопряженная матрица
, для которой сопряженная матрица ![]() , называют унитарной.
Иначе, квадратную матрицу
, называют унитарной.
Иначе, квадратную матрицу ![]() называют унитарной,
если выполнены условия
называют унитарной,
если выполнены условия
![]()
В
унитарной матрице столбцы (строки) составляют ортонормированную систему
столбцов (строк). Произведение унитарных матриц является унитарной матрицей.
Унитарные матрицы обладают и другими важными свойствами. Здесь существенным
является то, что матрицей перехода от одного
ортонормированного базису унитарного пространства к другому
ортонормированному базису является унитарная матрица. Очевидно, действительная
унитарная матрица является ортогональной. [3]
Литература:
1. Шевцов Г.С. Линейная алгебра..- М.: Гардарики,
1999.-359с.
2. Воеводин В.В. Линейная
алгебра. М.:Наука, 1974.-314с.
3. Гельфанд И.М. Лекции по линейной алгебре.-М, Наука, 1971.-71с.