К.ф.-м.н. Нечипоренко Н.А., к.ф-м.н. Белая Н.И.

Запорожский национальный технический университет, Украина

Численное дифференцирование сеточных функций, заданных с погрешностью

Рассмотрим задачу вычисления производной функции , которая задана своими значениями на равномерной сетке Значения известны с погрешностью , то есть имеют место неравенства

,

и значение известно. Необходимо вычислить значение производной в узлах сетки , используя указанную информацию. Известно [1], что задача численного дифференцирования функций, значение которых возможно иметь лишь с какой-нибудь погрешностью, является некорректной, поэтому нуждается в специальных алгоритмах.

К значениям функции применим алгоритм, который сглаживает эти значения и базируется на методе невязки. Значения вычисляются по разностной формуле с использованием сглаженных значений. Вектор сглаженных значений функции является решением такой экстремальной задачи:

(1)

при ограничениях

(2)

Задача (1)-(2) может быть сведенна к решению следующей задачи линейного программирования:

(3)

при ограничениях

, (4)

(5)

где

Задача (3)-(5) решается методом последовательного улучшения [2]. За начальное приближение берем вектор , то есть на первом шаге будет лишь одно активное ограничение. На каждом следующем шаге число активных ограничений (а, значит, и активных переменных) увеличивается на единицу. На s-ом шаге метода последовательных улучшений необходимо решать две системы алгебраических уравнений порядка s. Ограничения (5) учитываются алгоритмически, активными являются лишь ограничения системы неравенств (4). Поэтому матрица системы алгебраических уравнений имеет такую структуру ( при соответствующем упорядочении строк и столбцов системы): первые s-1 строка имеют каждая не больше 3 ненулевых элементов, а последняя строка составляется из единиц. Учитывая указанную особенность матрицы, возможно решать систему линейных алгебраических уравнений со значительной экономией памяти и числа операций. Расчеты показали, что при решении системы число ненулевых элементов увеличивается менее, чем в два раза.

Для решения задачи линейного программирования (3)-(5) возможно также использовать метод последовательного улучшения с пересчетом обратной матрицы. В этом случае количество операций на каждом шагу, бесспорно, уменьшается, однако, большие погрешности пересчета обратной матрицы при замене строк и столбцов приводят к значительным отклонениям в решении. В этом смысле метод последовательных улучшений намного точнее.

Матрицу ограничений (5) нет необходимости сохранять в памяти компьютера, необходимые значения элементов матрицы вычисляются при помощи вызова соответствующей функции.

После того, как найден вектор - решение задачи (3)-(5), сглаженные значения функции вычисляются по формуле:

,

при этом

Значение производной в узлах вычисляются по одной из разностных формул:

.

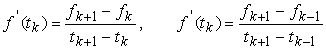Если известна оценка второй производной , то имеем следующую оценку погрешности вычисления производной:

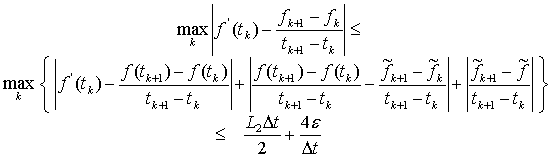
где .

Ясно, что перед решением задачи, если N довольно большое, следует увеличить шаг сетки , уменьшая тем самым число N.

Проведенные расчеты с использованием приведенного алгоритма показали его эффективность.

Если о функции известна некоторая качественная информация, а именно, интервалы, на которых функция возрастает или убывает, и (или) интервалы выпуклости функции, то использование этой информации позволит значительно улучшить качество аппроксимации производной. В этом случае к неравенствам (2) добавим такие:

(6)

(7)

здесь и могут принимать значение 1 или 2 в зависимости от возрастания или убывания функции при и в зависимости от вида выпуклости функции соответственно. - количество интервалов монотонности функции, - количество интервалов монотонности производной функции.

Замена переменных сводит задачу (1), (2), (6), (7) к задаче линейного программирования (3) при ограничениях (4), (5) и

(8)

(9)

где .

Решение последней задачи линейного программирования может быть осуществлено так же, как и задачи (3)-(5). Матрицы алгебраических систем сохраняют свою структуру. В этом случае немного увеличивается количество шагов метода последовательного улучшения и порядок систем алгебраических уравнений на последних шагах.

Литература:

1. Морозов В.А. Регулярные методы решения некорректно поставленных задач. – М.: Наука. гл. ред. физ.-мат. лит., 1987. -240с.

2. Булавский В.А., Звягина Р.А., Яковлева М.А. Численные методы линейного программирования. – М.: Наука, 1977. – 368с.