О надежности схем в базисах, содержащих функции специального вида

Васин А.В., Макаров Н.А.

(Пензенский государственный университет)

Считаем, что схема из ненадежных элементов реализует булеву функцию f(x₁, x₂, ..., x_n), если при поступлении на входы схемы набора = (a₁, a₂, …, a_n) при отсутствии неисправностей в схеме на ее выходе появляется значение . Обозначим – вероятность ошибки на входном наборе схемы A, реализующей функцию f. Число назовем ненадежностью схемы S. Надежность схемы S равна 1–P(S).

Пусть , где инфимум берется по всем схемам S из ненадежных элементов, реализующим функцию f(x₁, x₂, ..., x_n). Схема A из ненадежных элементов, реализующая функцию f, называется асимптотически оптимальной по надежности, если при e ® 0, т. е. .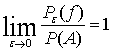

Булевы функции и назовем конгруэнтными, если одна из них может быть получена из другой заменой переменных (без отождествления). Пусть
– произвольное множество функций зависящих от переменных . Обозначим – множество всех функций, зависящих от переменных , каждая из которых конгруэнтна некоторой функции множества .

Введем следующие множества функций.

,

,

,

.

В работах [2], [3], [4] показано, что при инверсных неисправностях на выходах элементов наличие любой из функций множеств G₁, G₂, G₃, G₄, в заданном конечном полном базисе B гарантирует реализацию произвольной булевой функции схемой , функционирующей с ненадежностью , где , - некоторые константы.

В [5] было найдено множество функций M зависящих от n переменных, и показано, что наличие в базисе функций из множества дает аналогичный результат.

Вопрос о существовании других функций дающих такой же результат остается открытым.

Опишем множество G функций , также обладающих свойством повышения надежности. Пусть , где – вектор имеющий ровно одну ненулевую компоненту, равную 1, на i-том месте, .

Зададим множество , состоящее из 4 векторов , следующим образом:

1. , .

2. 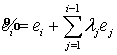, где – коэффициенты, .

Пусть существуют такие двоичные наборы такие, что 1) , ; 2) для любого набора такого, что , верно ; 3) для любого набора такого, что , верно ; 4) , где , .

Множество функций всех возможных функций , а также функций, из которых отождествлением и переименованием переменных можно получить одну из функций , обозначим .

Теорема 1. Пусть полный базис В содержит функцию . Тогда любую функцию f в этом базисе можно реализовать схемой A с ненадежностью
P(A) £ при e £ .

Не трудно видеть, что если схема S содержит хотя бы 1 элемент, то ее ненадежность P(S) ³ e. Любая схема, реализующая функцию, отличную от тождественной, содержит хотя бы 1 функциональный элемент.

Следовательно, если произвольный базис B содержит хотя бы один функциональный элемент, реализующий функцию из множества G, то для почти всех функций f (функций, отличных от тождественных) асимптотически оптимальные по надежности схемы S функционируют с ненадежностью при .

Заметим, что описанное множество функций G содержит в себе все известные ранее функции, обладающие свойством повышать надежность схем.

ЛИТЕРАТУРА

1. von Neuman J. Probabilistic logics and the synthesis of reliable organisms from unreliable components // Automata studies, edited by Shannon C., Mc. Carthy J. Princeton University Press, 1956. (Русский перевод: Автоматы. М.: ИЛ, 1956. С. 68 – 139.)

2. Васин А.В., Асимптотически оптимальные по надежности схемы в полных базисах из трехвходовых элементов: диссертация … кандидата физико-математических наук: 01.01.09. ― Пенза, 2010. — 100 c.

3. Алехина М. А. Синтез асимптотически оптимальных по надежности схем. − Пенза: информац.-издат. центр ПГУ, 2006.

4. Аксенов С. И. О надежности схем над произвольной полной системой функций при инверсных неисправностях на выходах элементов // Известия высших учебных заведений. Поволжский регион. Естественные науки. − 2005. − №6 (21). − С. 42−55.

5. Алехина М. А., Аксенов С. И., Васин А. В. О функциях и схемах, применяемых для повышения надежности схем // Известия высших учебных заведений. Поволжский регион. Физико-математические науки. − 2008. − №3