Математика/ 5. Математическое моделирование

Ph.D. Lyashenko A.L.

National University of mineral resources «Mountain», Russia

DEVELOPMENT OF TRANSFER FUNCTION SPACE-APERIODIC MEMBER

In engineering practice widely used various methods of approximate simulation of transfer functions PIU submitted in a typical BSC a rational form, sometimes supplemented by links of pure delay.

The transfer functions were found to be initially in the form of an infinite series using the method of integral transformations, or presented them in Taylor series expansions, and in some cases in a series of images of different orthogonal functions, for example in the form of series Burman-Lagrange.

In [1] are the transfer functions for a number of spatially distributed parts:. space-level amplifier 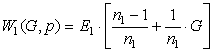ideal space-differentsiruschego management 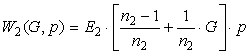, spatial and forcing managers 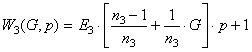, the ideal space-integrating element 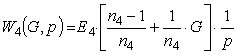and the space-PID member .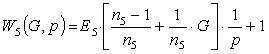

We introduce the space aperiodic member, it will develop and construct a transfer function frequency response.

For distributed spatially aperiodic member transfer function using the generalized coordinates, in accordance with the established procedure [1] can be written as follows:

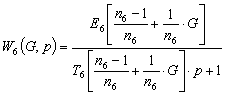
Where the overall gain (a given number) weighting, T6 - the time constant; G - generalized coordinate.

For analysis using frequency methods make the changein the transfer function, we obtain:

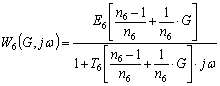
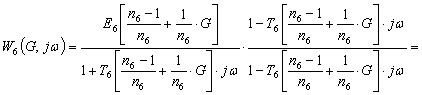
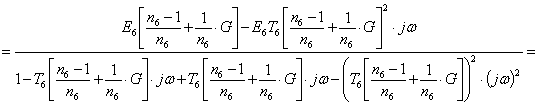
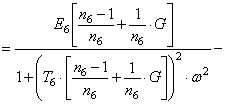
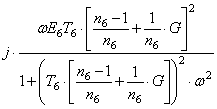
Consider the case where the weighting factor is unity.

When we get:

,

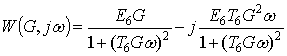when

, .

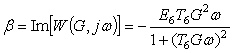Express the amplitude frequency response.

.

.

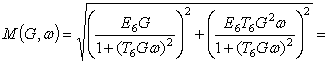
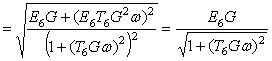With the help of Mathcad perform logarithmic amplitude-and phase-frequency characteristics.

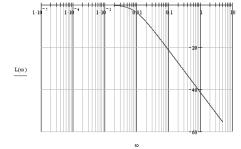
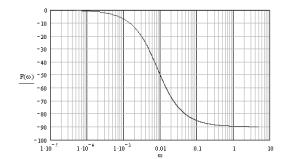
Fig. 1. Logarithmic frequency response and phase-frequency response

When you change the frequency w from 0 to ¥, and the values of the generalized coordinates G from G_н to ¥, vector W (G, jw) in the space Re (W), Im (W), G describes the surface, which is called the spatial locus.

Dimensional space-time-distance curve for aperiodic member is shown in Figure 2.

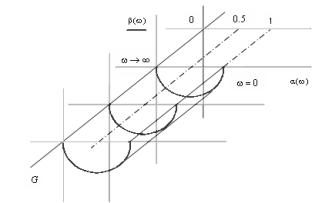
Fig. 2. Dimensional space-time-distance curve aperiodic member

Consider the case where the weighting factor is set to:

, , .

We make the construction of frequency characteristics.

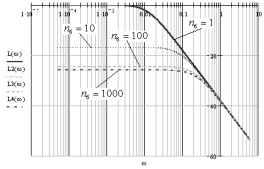
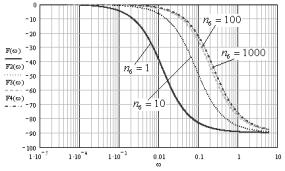
Fig. 3. Logarithmic frequency response and phase-frequency characteristics for , , ,

The developed method enables the output transfer functions for control objects with distributed parameters, obtain the transfer function space-aperiodic member can be used for the analysis of distributed objects, as well as for the synthesis of distributed control systems.

Literature:

1. Першин И.М. Анализ и синтез систем с распределенными параметрами. – Пятигорск, РИА КМВ. 2007. – 244с.