Функции когерентности

При селекции информативных сигналов

Гарькина И.А., д.т.н. проф., Данилов А.М., д.т.н. проф.

Простота информационной модели динамических систем определяется тем, насколько удается выделить наиболее существенные параметры, характеризующие состояние системы (без потери их изоморфности). Решение такой задачи требует системного подхода к формированию управляющих воздействий для повышения качества управления (селекция, ранжировка; определение иерархической структуры). Наиболее полно это представляется при проектировании имитаторов человеко-машинных систем. Здесь функция оператора состоит в формировании управляющих воздействий в результате сравнения информации о состоянии объекта (через систему отображения информации) с концептуальной моделью. В целях минимизации аналитической деятельности оператора в информационную модель должны включаться лишь наиболее существенные параметры состояния системы (множество информационных моделей состояния объекта должно быть изоморфно множеству состояний управляемого объекта). Это позволит снизить приобретение ложных навыков при использовании наиболее простых обучающих и тренажных комплексов для подготовки операторов.

При возможности формализации источников информации (неформализованные источники предполагаются априори существенными) для селекции информативных сигналов можно использовать выборочные функции когерентности 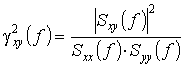. Функция когерентности является аналогом коэффициента корреляции в частотной области и отражает степень линейной взаимосвязи гармонических компонент рассматриваемых процессов. Такой способ селекции обладает наглядностью получаемых результатов и очевидным физическим смыслом.

Знание оператором в каждый момент времени состояния объекта позволяет ему приближенно осуществить заданное движение на основе формирования управляющих воздействий (обобщенный вектор управления). При формализуемых входных сигналах легко установить их связь с каждым из управляющих воздействий .

Так, при ,

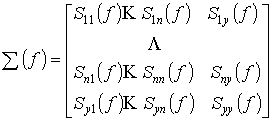
функция множественной когерентности на частоте :

.

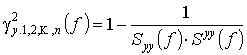Здесь , - взаимные спектральные плотности и , а также и соответственно; - спектральная плотность ; - последний элемент главной диагонали матрицы , обратной к ; , комплексно сопряжена с .

Справедливо:

.

Чем ближе значение функции множественной когерентности к 1, тем ближе связь между и всеми к линейной; если , то связь отсутствует. При связи являются линейными:

;

-линейные стационарные операторы; - стационарный процесс, не связанный на всех частотах с процессами (функция множественной когерентности между и равна нулю). Процесс можно рассматривать как процесс, полученный из путем исключения линейного эффекта компонент :

.

Процесс полностью когерентен компонентам , а полностью не когерентен .

Однако теоретически величина функции множественной когерентности не всегда служит хорошей характеристикой связи между и . Поэтому для получения надежных результатов о связи между и лучше использовать функцию условной (частной) множественной когерентности. Она позволяет установить, в какой степени на частоте связана линейным стационарным оператором после того, как из исключено влияние линейных, не зависящих от времени связей с другими составляющими .

Функция частной множественной когерентности определяется в виде:

,;

, ,

, .

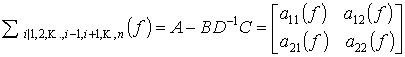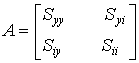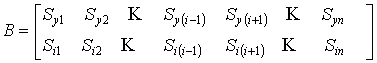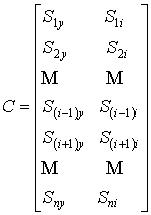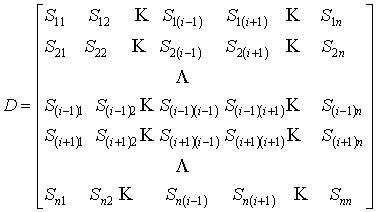Из предыдущего непосредственно следует:

,

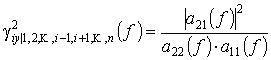(для определения передаточных функций человека-оператора целесообразно использовать соотношение ).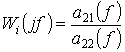

Таким образом, для селекции информативных сигналов и их ранжировки необходимо:

- произвести синхронные измерения сигналов и в процессе нормальной эксплуатации;

- определить элементы матриц ;

- вычислить элементы матрицы и для каждого значения определить функции частной когерентности

;

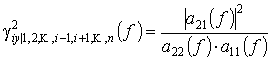- расположить в порядке убывания значений функций частной когерентности (чем больше информационная значимость сигнала, тем выше его ранг).

Заметим, что не всегда по данным нормальной эксплуатации можно установить, какие из процессов являются входными, какие - выходными (часто следствие принимается за причину); требуется когнитивное моделирование с построением орграфа (относится не только к замкнутым системам). В некоторых случаях направление «вход-выход» можно установить по расположению максимумов взаимных корреляционных функций. Если взаимная корреляционная функция достигает максимума при , то входом следует считать ; при - .

Подчеркнем также, что линейные зависимости, устанавливаемые по функциям частной когерентности, не обязательно единственны.

Возможности адаптации приведенной методики ранжировки входных сигналов для формирования управляющих воздействий очевидны и не требуют дополнительных пояснений.