Математика/ 4. Прикладная математика

Ардашева М.В., Самойлова И.А.

Карагандинский государственный университет имени академика

Е.А. Букетова, Казахстан

Применение среды разработки Lazarus к приближенному решению нелинейных уравнений

Точные решения некоторых уравнений, таких как квадратные, тригонометрические, линейные получают путем равносильных преобразований алгебраических выражений. Для большинства же уравнений удобно использовать метод приближенного решения с некоторой заданной точностью. К таким методам относятся графический и численный.

Численное решение можно осуществить путем использования классического приближенного метода половинного деления. Данный метод является несложным и довольно надежным способом нахождения корней нелинейного уравнения. Суть метода состоит в выборе точности решения и сведении исходного отрезка , на котором существует корень уравнения, к отрезку выбранной точности. Причем компьютерная модель позволяет задавать достаточно большую точность. Далее весь процесс сводится к последовательному делению отрезков пополам точкой, равной половине отрезка , т.е. . Проверка знаков значений заданной функции позволяет выбрать необходимую половину отрезка ( или ). Выбираем ту половину, на которой функция меняет знак. Для этого необходимо проверить условие: произведение значений функции на краях отрицательно. Процесс продолжается до тех пор, пока длина отрезка не станет меньше удвоенной точности. Деление этого отрезка пополам дает значение корня с заданной точностью.

Пусть перед нами поставлена следующая задача: найти решение уравнения на отрезке [0;1], с точностью = 0.001.

Для реализации численного решения приближенного метода половинного деления разработаем компьютерную модель на языке Lazarus.

Lazarus - свободная среда разработки программного обеспечения для компилятора Free Pascal на языке Object Pascal. Интегрированная среда разработки предоставляет возможность кроссплатформенной разработки приложений в Delphi-подобном окружении. На данный момент Lazarus является доступным инструментом быстрой разработки приложений, позволяющим пользователям создавать графические и консольные приложения.

Поместим на форму:

· четыре надписи Label для вывода обозначений (постановки задачи; начала и конца отрезка, точности вычислений);

· надписи Label5, Label6 для вывода корня уравнения;

· текстовые поля Edit1, Edit2 для задания начала и конца отрезка;

· текстовое поле Edit13 для задания точности вычисления;

Поместим также на форму кнопку Button1 и создадим событийную процедуру TForm1.Button1Click:

После запуска программы появится приложение:

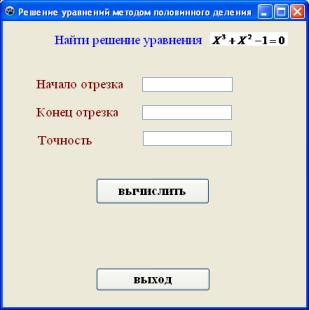
Введем в поля редактирования исходные данные поставленной задачи и нажмем на кнопку «Вычислить», получим следующее:

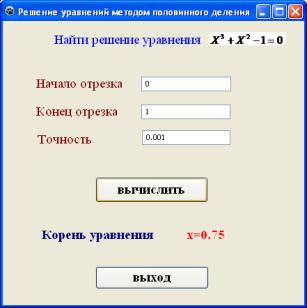
Точность вычисления корня зависит не только от параметров используемого численного метода, но и от типа переменой. В данном случае имеет место математическая точность результата, которая не может превышать точность числового метода, т.е. x=0.75.

Графическое решение тоже можно реализовать посредством построения компьютерной модели на Lasarus, например, построить график заданной функции, что позволит наглядно продемонстрировать ее поведение на заданном отрезке:

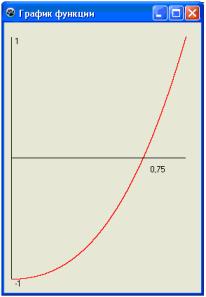
С помощью языка программирования Lazarus предлагается найти корни уравнений:

а) на отрезке (ответ: );

б) на отрезках и (ответ: ) с той же точностью = 0.001.

Отличительной особенностью применения данного метода на уроке математики является то, что решение уравнения учащиеся получают с помощью численного и графического методов, реализуемых с помощью объектно-ориентированного языка программирования Lazarus. А это должно способствовать развитию познавательного интереса не только к уроку математики, но и к информатике.

Литература:

1. Мансуров К.Т. Основы программирования в среде Lazarus, 2010.

2. Вержбицкий В. М.. Численные методы. Линейная алгебра и нелинейные уравнения. Издательство: Оникс 21 век, 2005.

3. Угринович Н.Д. Учебник для 11 класса. «Профильный уровень.» - 3-е изд. - М.: Бином. Лаборатория знаний, 2010.