Ïåäàãîãè÷åñêèå íàóêè/
ñîâðåìåííûå ìåòîäû ïðåïîäàâàíèÿ
Ê. ï. í. Òðîôèìîâà Ë. Í.
Îìñêèé óíèâåðñèòåò ïóòåé ñîîáùåíèÿ
Two approaches to the study of
mathematics in high school (Russia, Germany)
For
centuries mathematics became to the integrated part of school education in all
over the world. Mathematics as the science is promoting of intellectual
development, formation of logic, abstract thinking and intuition.
By
russian standarts [3] the main tasks of mathematical education were determined:
·
obtaining a system of mathematical knowledge
and skills which are necessary to apply in practice, study related subjects and
continuing education;
·
intellectual development, formation of
personal skills necessary for a normal life in modern society: clarity and
precision of thought, critical thinking, intuition, logical thinking, elements
of algorithmic culture, spatial concepts, ability to overcome difficulties;
·
formation of the concept concerning ideas
and methods of mathematics as a universal language of science and technology
and intrument for modeling of phenomena or processes;
·
growing of the culture of
personality, viewing to mathematics as part of human culture, the understanding
of the importance of mathematics for scientific and technical progress.
German mathematical education
seeks to ensure that the student appeared able to understand the importance of
mathematics in the modern world and to be able to apply mathematical methods in
their daily activities [4].
In Germany high school
graduate should have the following mathematical skills:
· to determine
of the problems in reality which can be solved by mathematics;
· to formulate
these problems using the language of mathematics;
· to solve
these problems using mathematical knowledge and techniques;
· to analyze
of the used methods;
· to interpret
of the results in the perspective of the problem;
• to organize and record the
final results of the task.
The
success of mathematics-study strongly depends on the content of classbooks or textbooks. To the problem of
writing of the textbooks in mathematics has always paid great attention in
science, teaching and methodical literature.
In this work we
have analyzed the main sections of mathematical textbooks for high school
published in Russia and Germany [1], [2]. We took for analysis only the
relevant sections of textbooks. The main purpose of our research is to
determine the suitability of modern mathematical textbooks to the tasks of
school mathematical education.
For the analysis
we used the following criteria:
- Scientific and
systematic exposition of the theoretical material;
- Accuracy of the
statements and the establishment of concepts and definitions;
- The ratio of
theoretical and practical material;
- Applied
direction of exercises and tasks;
- Simplicity of
presentation of the educational material;
- Clarity and
brevity in presentation of the theoretical material;
Table 1 shows the main
sections of the German and Russian textbooks in mathematics recommended by the
ministries of education in these countries.
|
Sections to be studied in a German textbook |
Sections to be studied in a Russian textbook |
|
Function
analysis using derivative |
Function
analysis using derivative |
|
The
use of differential calculus |
The
use of differential calculus |
|
Fundamentals of integral calculus |
Fundamentals of integral calculus |
|
The
use of integral calculus |
The
use of integral calculus |
|
The rules for finding
the derivative, derivative of a composite function |
The rules for finding
the derivative, derivative of a composite function |
|
Trigonometric functions |
Trigonometric functions |
|
Elements of
Probability theory |
Elements of
Probability theory |
|
Random
variables and probability distributions |
Random
variables and probability distributions |
|
Exponential
function |
|
|
System of linear
equations |
|
|
Vector |
|
|
Straight line in space |
|
|
Scalar
multiplication |
|
|
Matrix |
|
|
|
The real numbers. Infinitely decreasing geometric progression. nth root. Exponentiation by a real index |
|
|
Exponential
function |
|
|
Logarithmic function |
1. Power function. Analysis
of the function with the use of derivatives.
«Power function» and «Analysis of the
function with the use of derivatives» are Separate topic in Russian textbook
[1, C. 39-67, 257-279].
In
the given textbook discusses in detail the different cases of the power
function ![]() :
:
1. Index ð=2n is even natural number.
2. Index ð=2n-1 is odd natural number.
3. Index ð=-2n, where “n“ is natural number.
4. Index p= -(2n-1), where “n“ is natural number.
5. Index p – positive real noninteger.
6. Index ð – negative real noninteger.
For
each case domain of a function, range, intervals of increase and decrease of
the function are determined.
The graph of the function for a particular case is drawn.
Then the exercises for training are offered:
- to sketch the graph of function and to find domain of a function and it’s range;
- to identify the intervals of increase and decrease
of the function;
- to compare numbers using the properties of power
functions;
- to find the coordinates of the crossing points
of functions graphs.
All exercises are overly theoretical.
There are no tasks with practical content.
“Function
analysis using derivative” is a final paragraph in section ”Derivative” in case
of Russian textbook.
Before proceeding to the study of functions the
students need to learn the concept of derivative, the geometrical and physical
meaning of derivative, the continuity of function and the equation of tangent.
All "approaches" to all formulas concerning
these concepts demonstrated using the limit.
There are many formal definitions.
During the study of some subject the proofs of the
theorems taking place also.
In the 47-page textbook 34 pages are provided on
theoretical material.
All the exercises are theoretical and there are
no practical tasks.
In
German textbook the paragraph “Power function”[2, C.13-22] considered as a part
of section ”Analysis of the function with the use of derivatives” while
consideration of the theme begins with a practical example.
Traffic on the roads occurs regularly during the holiday season. This
traffic occurs due to objective reasons sometimes. This may happens when the
road is under construction for example. Then the traffic flow have to be
restructured from several lines into two or just one. To avoid this it is
necessary to determine the recommended speed which vehicles have to use per
unit of time to pass this section of road. And it is aslo necessary to pay
attention that if the vehicle is moving too slowly it will hamper the movement
of other vehicles behind.
At the too high speed the limit of designated safe distance between
vehicles is becoming too small which increases the accident rate on this part
of road. The vehicle must keep some sufficient distance from other vehicles for
safety. This distence is 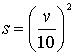 . Vehicle length is 5 meters. Task is to determine the optimal speed of
the car in case of the traffic.
. Vehicle length is 5 meters. Task is to determine the optimal speed of
the car in case of the traffic.
The formal model
in the view of a power function is creating and after that it have to be
analyzed.
This example is
relevant to the modern world of course but authors have made a mistake.
This function was
taken as the model: 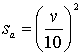 , where
, where ![]() distance measured in meters; v – speed [km/h].
distance measured in meters; v – speed [km/h].
In this case the
question arises. From the physical point of view what is the value of 10? According to the logic of the problem we see
that: 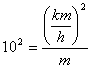 . Such physical quantities we've never seen before.
. Such physical quantities we've never seen before.
There are four
cases of the power function are under the attantion in the given textbook:
1. Index
ð=0.
2. Index
ð=1.
3. Index ð=2n – even natural number.
4. Index ð=2n-1 – odd natural number.
Clearly
illustrated the dynamics of the function during of the index changing.
The main stages
of the function analysis are clearly and concisely theoretically shown in the
table: symmetry, zero of a function, local maximums and minimums, concavity,
convexity, the ploting of the function. The meanings of tangent
and normal are explained.
There is an approach:
t(x)=mx+n
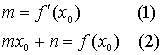
In our opinion,
(2) is represented in not quite correct view.
Probably a better
variant would be as following:
![]()
There is a lack
of some geometric interpretations: concept of tangent as the limiting position
of the secant, variable m as the
angle of the tangent, variable n as
the length of the segment which cuts off by tangent on the vertical axis (OY) from zero.
This topic
contains four examples (one of them contains a practical sense - a game of
mini-golf).
There are several
self-paced exercises.
At the end of the
topic is a brief theoretical overview of the studied material and and there is
also a final test.
2. Using of the derivative.
Regarding
the using of the derivative, in german textbook many of them are considered in
relation to the practical point of view [2, C. 32-54].
9
examples are given for purpose to find the maximum area (m2) using
the given conditions. For example the following.
Somebody has a cable
length of 800 meters. It is necessary to enclose a rectangular area of land
from three sides (one side is a sea coast). The textbook offers to calculate
the optimal area of this space. It is should be maximal.
In
addition there are four tasks concerning geometrical limitations (finding the
maximum and minimum values).
Using the round timber having
a diameter of 40 cm to saw out the square timber with maximum amount of it’s
weight.
In
our view this is also not very good example. It is fine that the authors of the
textbook need for such tasks where there is only one variable. In this case it
was possible to consider the task like that... Need to saw out the square timber. Cross-sectional area should be
maximal.
The
textbook also have some tasks solving the problem of finding the optimal size
of the package for matches.
Then
followed another 15 tasks to consolidate of knowledge. In the introduction the
authors paid attention that this section provides a large number of tasks and
it is not necessary to do all these exercises. However, we feel that it would
be appropriate to put this part after the section "Derivative of a composite
function". Then there was an opportunity to show the practical problems
that are solved using of different functions and not just with a simple power
law. Then in the example with a point on the screen would be better to just get
the function 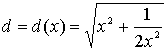 and do not to convert this to a strange
function
and do not to convert this to a strange
function ![]() and to calculate the derivative from it. The
derivative from d(x) would
have been enough.
and to calculate the derivative from it. The
derivative from d(x) would
have been enough.
In
this paragraph the transition from the derivative to the optimization tasks
using a system of linear inequalities is looks surprising. The relationship
between the derivative and the system of linear equations is not quite clear.
The
paragraph on "Recovery of function" is very interesting in our
opinion. Some values of the function: the value of the derivative
at a given point, the zeros of fuction, etc. are presented. Using these
conditions is necessary to restore the original view of equation. Such problems
are, of course, contribute to the development of logical thinking.
The
Russian textbook there are two sections showing the examples of the derivative
application: "Using of derivatives to plot the graphs of functions"
and "Using of derivative and integral to solve practical problems"[1,
C. 305-314].
The
paragraph “Practical application of the derivative” begins by introducing the
concept of a differential equation. Then the two equations are solved in a
general way. To illustrate the solution the examples are providing: relationship between speed of bacteria
reproduction and mass of bacteria, equation of harmonic oscillation. In our
opinion there are quite difficult formulated tasks. They are may be interesting
for specialists in certain areas but not for school pupils. In this textbook
there is a lack of simple tasks aimed to the practical content. Just such an
excess in the German textbook.
3.
Fundamentals of integral calculus.
The
consideration of section “Integration” in German textbook [2, C. 70-75] begins
with the following example: for given type
of function ![]() , it is necessary to determine the derivative of which
function is it.
, it is necessary to determine the derivative of which
function is it.
Empirically, there are a variety of answers: ![]() and a total solution for all is
recorded in this view:
and a total solution for all is
recorded in this view: ![]() , where C is the
constant of integration. After that gives a definition of antiderivative.
, where C is the
constant of integration. After that gives a definition of antiderivative.
This task in our
opinion is very interesting from the point of the pupil's thinking on the
issue.
How to determine the original function using the given derivative?
Next step in
texbook is examples of integral finding and description of the integral
properties and showing of joint properties for the integration and
differentiation.
Illustrates the
geometric meaning of the constant of integration.
Then offers the
tasks for independent work: to calculate
the integral, to find the antiderivative for a given function.
The conception of
integral is explained as the sum of an infinite number of the rectangles areas.
It is shown that
if the figure has a complex configuration, before finding an area it is
desirable to mentally cut the figure for a few simple shapes.
Then shows
specific examples. The properties of the definite integral are also considered
in textbook. Offers examples for individual work.
As material for
further study the numerical methods for finding the area of a
rectangle (the method of right and left rectangles) are presented. The final
section summarizes the theoretical material in the form of test. 14 pages are
discharged to this section. This section provides a brief, clearly, maintaining
mathematical rigor.
The section
"Integration" in the Russian textbook [1, C. 287-311] begins with the
task: how to find a path traversed by a
point based on point moving speed. (that is to say – how to determine the
function s(t) knowing its derivative v(t)).
This task is not
correct, because if we put the punctuation mark
“full stop” at the end of the phrase "
how to find a path traversed by a point based on point moving speed "
we will find the absurd.
The example given
in the German textbook, more successful, more clear and understandable.
Further, the Russian textbook gives
a explanation of antiderivative and one example: how to prove that the given functions ![]() are antiderivatives of function
are antiderivatives of function ![]() . Based on this example the concept of the integration constant “C” is
introduced and explained; introduced so poorly, too theorized and too
difficult.
. Based on this example the concept of the integration constant “C” is
introduced and explained; introduced so poorly, too theorized and too
difficult.
Then several examples for individual work are
offers.
In the next section we can see the
rules how to find the antiderivative and some tasks for independent work.
Paragraph
"The area of the curvilinear trapezoid and integral" begins with the
definition of a curvilinear trapezoid, then theoretically substantiated that
the area of the curvilinear trapezoid is the definite integral.
Again it is necessary to focus the attention on the complexity of presentation
and excessive formality. It is not clear why the pupil must to know the concept
of "integral sum" at first acquaintance with the concept of the
definite integral. In the textbook there are paragraphs: "Calculation of
integrals" (only definite integrals are considered), "Calculating of
the areas using the integrals". Why not combine them into one and call
this a "Definite integral"? From a geometrical point of view the
definite integral is the area of the curvilinear trapezoid. As a result 24
pages of textbook are dedicated to the section "Integration". Based
on a comparison with the German textbook, the Russian textbook material
concerning this topic is presented very poorly.
4. The application of integral calculus.
"The
application of integral calculus" is a independent section in the German
textbook [2, C. 86-109]. It begins with a consideration of the possible
variants of the figure location (the area of this fugures has to be
calculated).
Three cases are
considerated:
1. figure is
above the x-axis;
2.figura located
below the x-axis;
3. part of the
figure is below the x-axis, the other symmetric part lies above the x-axis.
In our view, the
third case deserves more attention than it was realy paid by authors. The
authors are considering an example: 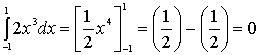 It
turns out an apparent contradiction. On the one hand a pupil sees schematically
figure and understands that this figure has a specific area. On the other side
of the definite integral is zero. Paradox! This example requires a logical conclusion. It was necessary to show
that if part of the figure is below the x-axis and the other is above the
x-axis, then the limits of integration must be divided into the separate
sections. Then you need to calculate the module of the integrals at each site
and sum up the obtained values. Indeed the other examples are discussed in this
order. So why it is not done at once?
It
turns out an apparent contradiction. On the one hand a pupil sees schematically
figure and understands that this figure has a specific area. On the other side
of the definite integral is zero. Paradox! This example requires a logical conclusion. It was necessary to show
that if part of the figure is below the x-axis and the other is above the
x-axis, then the limits of integration must be divided into the separate
sections. Then you need to calculate the module of the integrals at each site
and sum up the obtained values. Indeed the other examples are discussed in this
order. So why it is not done at once?
A variety of some
practical tasks aslo deserve the attention. These exercises are interesting in
content and not so difficult from a mathematical point of view. To the Russian
authors of mathematical textbook I would like to recommend to study in detail
the experience of German colleagues in the preparation of tasks with practical
content.
I’d like to
represent another exercise of the German textbook.
The tunnel is ventilated by two fans. The performance of each of them is
about 80 cubic meters per minute. How much time is needed for completed
replacement of the air inside the tunnel?
There are raw data: the length of the tunnel is 60 meters, width is 20
m, height is 8 meters and domed roof, represented by the equation of a
parabola. The distance from the upper point of the roof to the rectangular base
is 10 meters.
5. The rules for finding the derivative. Derivative of
a composite function.
The topic in German textbook [2, C.
120-136] begins with a discussion of the question: How to find the derivative of multiplication. The authors draw an
analogy with the derivative of the sum. They making the assumption that the
derivative of the multiplication will be equal to the multiplication of the
derivatives. Then the given example shows fallacy of this assumption. Probably
it would be more successfully if the authors have shown a formula for finding
the derivative of the multiplication at first and then researched or given to
home-review that example which shows that the derivative of multiplication is
NOT equal to the multiplication of the derivatives. Formula for the derivation
is created not correctly. Written definition of the derivative: ![]() , and then after
equality sign is written expression:
, and then after
equality sign is written expression: ![]() . It would be good to know how there
was a transition?
. It would be good to know how there
was a transition?
Derivative
of fraction are derived based on the derivative of multiplication. The
derivative of a composite function is considered as an example of the power
function. The derivative of a composite function is considered based on example
of the power function.
For
consolidation and completion of the material following tasks are offered: to
find the derivative of a function at some point, to show the equation of the
tangent, extremums, zeros of function, etc. Thus the previously learned
material is repeated and fixed.
In
the same paragraph the integral of the power function when the base is a
combination of linear functions. At the conclusion of this paragraph is a brief
summary of the theoretical material and provides a practical example.
The
part “Differentiation rules. Derivative of a composite function” also
considered in the Russian textbook [1, C. 236-251]. Formulas for the derivative
of summation and fro the derivative of
multiplication (function × Constant) are creating thought the limits.
Formulas for derivative of multiplication and derivative of fraction in their
origin are not shown.
For
the homework some tasks are proposed:
to find the derivative of a function at a point;
to find the intervals where the derivative is greater than zero or less
than zero;
Practical tasks
are required the knowledge of physics and chemistry. All of them are considered
by the example of the power function. This tasks are little bit difficult in
its formulation for non-specialist.
We saw two very
different approaches to the study of mathematics: "Theoretical and
formal" in Russia and "Practice-simplified" in Germany.
In our view the
presentation of material in Russian textbooks too formalized, devoid of
clarity. The theoretical material is too large in comparison to the
exemplified. There is a lack of applied examples that demonstrating the
importance of studying the topic. During the looking into a textbook the
question are formed: Why should we learn it? Where it can be useful? Readers
can only assume that it is necessary for the further study of mathematics.
The textbook
published in Germany is obvious. It contains many life-examples, the simplicity
and brevity of theoretical material.
In our opinion
there is only one drawback in this textbook.
Trying to explain
the theoretical material in an accessible form for a pupil, the authors lost
accuracy of presentation and compliance of the presented material to
mathematical sense.
References:
1. Alimov S. A.,
Kolyagin Y. M. Algebra and calculus: High Schools 10-11 class. M.:
Prosveschenie, 2012. – 463 c.
2. Bigalke A.,
Kohler N. Mathematik. High Schools. Berlin:
Cornelsen Verlag, 2011. – 560 c.
3. Standard of
general education in mathematics. Russia. [Electronic resource] access mode: www.school.edu.ru.
4. Standard of
general education in mathematics. Germany. [Electronic resource] access mode: www.standardsicherung.de.