Педагогические науки/5. Современные методы преподавания

Асканбаева Г.Б.

Костанайский государственный университет им. А. Байтурсынова, Казахстан

Графы в нестандартных задачах

Задача считается нестандартной, если для ее решения требуется применить нестандартные методы решения. Такие виды задач в основном представляются для решения в математических олимпиадах, которые очень часто проводятся как среди школьников, так и среди студентов. Основная задача олимпиадного движения – пропаганда математических знаний среди молодежи, подготовка к будущей научной деятельности, заострение интеллекта. В данное время достаточно часто выпускаются сборники олимпиадных задач, для множества из них рационально применять графическое решение.

Чтобы студенты увлекались решением математических задач, необходимо их заинтересовать, а это сделать достаточно нелегко. Но если задача увлекательна, то интерес к ней, независимо от желания студента, мобилизует его умственную энергию, облегчает запоминание. Представленные в статье задачи полностью отвечают этим требованиям, т.к. они интересны, необычны и развивают особое мышление, большинство привлекают к себе внимание уже начиная с прочтения и условия, многие из них используют в своей основе литературные сюжеты, многие ситуации из жизни.

В данной статье рассматриваются задачи, при решении которых используется теория графов.

Особо требуется выделить задачи рамсеевской теории граф, где рассматриваются задачи на раскраску графов.

О данной теории было опубликовано несколько статей в 30-х годах венгерским математиком Паулем Эрдешем и другими, серьезная работа по исследованию того, что теперь называется числами Рамсея, началась только в конце 50-х годов. Одним из стимулов исследования была невинно выглядевшая головоломка. Эту головоломку легко преобразовать в задачу о графах. Шесть вершин соответствует шести людям. Соединим пару вершин, соответствующих двум знакомым людям, красной линией, а пару вершин, соответствующих двум незнакомым людям, синей линией. Теперь задача состоит в том, чтобы доказать, что, как бы мы не выбирали цвета лини, у нас неизбежно получится или красный треугольник (соответствующий тройке попарно знакомых) или синий треугольник (соответствующий тройке попарно незнакомых).

Экономисты знают Рамсея за его замечательный вклад в экономическую теорию. Логики знают Рамсея за его упрощения разветвленной теории типов Бертрана Рассела и за придуманное им подразделение логических парадоксов на логические и семантические.

В 1928 году Рамсей сделал доклад в Лондонском математическом обществе по ставшей теперь классической работе «Об одной проблеме в формальной логике». В этой работе Рамсей получил глубокий результат о множествах, который известен теперь как теорема Рамсея. Оказалось, что эта теорема, подобно многим теоремам о множествах, имеет большое число разнообразных неожиданных применений к комбинаторным задачам. Мы рассмотрим, как эта теорема применяется в теории раскрашивании графов.

Если каждая из n вершин соединена линией с каждой другой вершиной, то граф называется полным графом с n вершинами и обозначается символом . При этом для нас неважно, как именно расположены вершины и проведены линии.

Предположим, что мы произвольным образом раскрасили линии графа в красный или синий цвет. Мы можем раскрасить все линии в красный цвет, раскрасить все линии в синий цвет или использовать оба цвета. Такая раскраска называется 2-раскраской графа. 2-раскраской есть, конечно, простой способ разбиения всех пар из наших n вершин на два непересекающихся класса. Аналогично, 3-раскраска линий разбивает эти пары на три непересекающихся класса, и вообще, r-раскраска разбивает пары вершин на r попарно непересекающихся классов.

Игры и головоломки Рамсея с меньшими полными графами и с карандашами только двух цветов могут быть вполне занимательными. Приведем задачу, которая решается непосредственно при помощи теории графов.

Задача. Докажите, что если каждый из пяти человек переписывается только с двумя другими, то не найдется трех человек, которые все переписываются между собой.

Доказательство: Рассматривается полный граф с пятью вершинами. Пусть синие ребра соответствуют двум переписывающимся людям между собой, а красные – не переписывающимся. Необходимо доказать отсутствие красного треугольника в таком графе. По условию, каждый человек из пяти переписывается с двумя другими, тогда получаем граф, представленный на рисунке 12. Остальные ребра могут быть только красными. Из этого следует, что в графе не существует треугольника с синими ребрами, то есть не найдется трех людей, переписывающихся между собой.

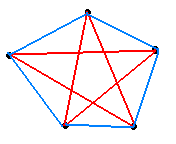
Рисунок 1

С помощью теории графов большинство задач решаются на много проще, чем логически.

Литература:

1. Берж К. Теория графов и их применение. Новосибирск, Наука, 1969, 581 с.

2. Оре О. Графы и их применение. М., Мир, 1965, 127 с.

3. Оре О. Теория графов. М., Наука, 1968, 321 с.