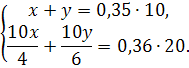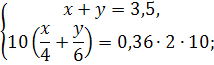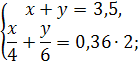к.п.н. Каллаур Н.А., ст. 5 курса Кирильчук Н.С.

Брестский государственный университет имени А.С. Пушкина

Применение межпредметной интеграции на уроках математики

Математика проникла практически во все сферы человеческой деятельности. Развитие современной науки, производства, информационных технологий невозможно без применения математических знаний. Поэтому большое значение имеет демонстрация учащимся уже в школьном курсе взаимосвязей математики с другими дисциплинами.

Изучение математики как науки в школе должно строиться не только на основе формирования у учащихся определенных математических знаний, но и должно показывать применение данных знаний для решения практических задач. Межпредметные связи на уроках математики можно реализовать посредством решения задач с физическим, химическим, географическим и другим содержанием. Такие задачи можно предлагать учащимся после объяснения новой темы по математике для того, чтобы показать практическое применение изученной теоремы, формулы, свойств. Для использования данного приема на уроках математики имеются большие возможности, так как большинство формул, теорем математики применяются при решении задач из смежных дисциплин.

Учителю требуется приводить конкретные примеры, факты из физики, техники и других дисциплин, особенно в начале изучения данного предмета, чтобы сформировать у учащихся верное целостное представление об этой науке. Важно, чтобы учащиеся понимали, что математика как наука моделирует реальную действительность и изучаемые ими математические понятия являются не абстрактными, а отражают реальные процессы, поэтому и применяются при решении задач других школьных предметов.

Приведем пример математической задачи с химическим содержанием.

Задача. Имеются два сосуда, содержащие соответственно 4кг и 6 кг раствора кислоты разных концентраций. Если их слить вместе, то получится раствор, содержащий 35% кислоты. Если же слить равные массы этих растворов, то получится 36% раствор. Сколько килограммов кислоты содержится в каждом растворе?

Учитель математики. Сначала рассмотрим математическое решение этой задачи.

Что нужно найти в задаче?

Что удобно обозначить через переменные?

Сколько вводим переменных?

Для нахождения значений переменных достаточно ли будет составить одно уравнение?

Значит, что нужно составить?

Давайте составим таблицу.

Пусть масса кислоты в первом растворе кг, а во втором – кг.

Чему равна массовая доля кислоты в первом растворе?

Во втором растворе?

Чему равна масса вещества, после того как слили два раствора и получили 35% раствор?

Как найти массу вещества в этом растворе?

Затем берут два раствора этих же концентраций, но равной массы. Для удобства дальнейшего счета давайте возьмем массу 10 кг.

Чему равна масса вещества в первом растворе?

Во втором?

После того как слили эти растворы, чему их масса равна?

Найдите массу вещества в получившемся растворе.

Какую можно составить систему?

Оформим решение задачи.

Самостоятельно находим значения .

Какой получили ответ?

Учитель химии. При решении этой задачи с точки зрения химии нам не обойтись без составления системы уравнений, но через переменные обозначим массовые доли кислоты в растворах. Пусть массовая доля кислоты в первом растворе – %, а во втором – .

Чему равна масса кислоты в каждом из растворов?

Чему равна масса кислоты, после того как растворы слили в один сосуд?

Какое получили уравнение?

Затем берут одинаковые массы каждого раствора. Пусть берут по 1 кг.

Чему равна масса кислоты в каждом растворе?

Чему равна масса кислоты, после того как растворы смешали?

Какое уравнение получили?

Какую систему надо решить?

Решив ее получите те же ответы.

Массу кислоты, содержащуюся в каждом растворе.

Массу кислоты в первом растворе и массу кислоты во втором растворе.

Две.

Нет.

Систему, содержащую два уравнения.

	Масса раство-ра	Массовая доля вещества	Масса вещества
1-ый раствор	4
2-ой раствор	6
1-ый + 2-ой	10	35
1-ый раствор	10
2-ой раствор	10
1-ый + 2-ой	20	36

4+6=10 (кг).

(кг).

20 кг.

Пусть масса кислоты в первом растворе кг, а во втором – кг. Для того, чтобы получить 36% раствор, взяли кг первого раствора и второго раствора. Зная, что масса вещества в 35% растворе 3,5 кг, а в 36% – 0,72 кг, составим и решим систему уравнений.

Значит, в первом растворе масса кислоты равна 1,64 кг, во втором – 1,86 кг.

Ответ: 1,64 кг, 1,86 кг.

– в первом растворе, – во втором.

3,5.

.

.

0,72.

Осуществление межпредметных связей на уроках математики может проходить в различной форме. Прежде всего, это связанно с различными видами межпредметных связей, среди которых выделяют предшествующие, сопутствующие и перспективные межпредметные связи. Данная классификация связана со временем применения понятий одного учебного предмета при изучении другого. Соответственно, либо используемые понятия уже изучались ранее в курсе другого предмета, либо также изучаются в данный момент времени, то есть параллельно, либо еще будут изучаться в будущем.

Использование межпредметных связей на уроках математики содействует внутрипредметной и межпредметной интеграции, использованию методов математики в разных областях научной и практической деятельности. В качестве одного из принципов отбора содержания учебного материала выделяется принцип интеграции. Такой подход позволяет сформировать представления о главном месте математики в системе наук, ее методологическом значении и роли в формировании общей культуры, осознание того, что средствами математики описываются и исследуются явления и процессы действительности.