Физика/1. Теоретическая физика
Ефремов
В.Е., Кузьмин М.К.
Московский
государственный областной университет, Россия
Решение гидродинамической задачи в
теории нестационарного диффузиофореза крупной твердой нелетучей сферической
частицы
В статье решается гидродинамическая задача
теории нестационарного диффузиофоретического движения крупной твердой нелетучей
частицы сферической формы с учетом диффузионного скольжения газа вдоль
поверхности частицы. Рассмотрим одиночную твердую нелетучую частицу сферической
формы радиуса R, взвешенную в
неоднородной по концентрации бинарной газовой смеси. Будем полагать, что мы
имеем дело с вязкой несжимаемой газовой средой. Пусть ![]() и
и ![]() - относительные
концентрации молекул бинарной смеси газов, имеем
- относительные
концентрации молекул бинарной смеси газов, имеем
![]() .
.
Будем
рассматривать первый компонент смеси в качестве диффундирующего. Обозначим
через ![]() ,
, ![]() средние длины
свободного пробега молекул первого и второго видов соответственно. Выбор метода
решения задачи построения теории нестационарного диффузиофореза твердой
нелетучей сферической аэрозольной частицы зависит от отношения средних длин
свободного пробега молекул газа к
размеру аэрозольной частицы [9]. Мы полагаем, что
средние длины
свободного пробега молекул первого и второго видов соответственно. Выбор метода
решения задачи построения теории нестационарного диффузиофореза твердой
нелетучей сферической аэрозольной частицы зависит от отношения средних длин
свободного пробега молекул газа к
размеру аэрозольной частицы [9]. Мы полагаем, что ![]() << 1,
<< 1, ![]() << 1, т. е., рассматриваем крупную сферическую частицу.
Поэтому в исследованиях привлекаем классические методы динамики сплошной среды
[6, 7]. При использовании уравнения Навье-Стокса предполагаем, что число Рейнольдса
мало.
<< 1, т. е., рассматриваем крупную сферическую частицу.
Поэтому в исследованиях привлекаем классические методы динамики сплошной среды
[6, 7]. При использовании уравнения Навье-Стокса предполагаем, что число Рейнольдса
мало.
Для частицы,
имеющей сферическую форму, математические выкладки удобно проводить в
сферической системе координат ![]() с началом в центре
частицы. На относительно большом удалении от частицы (r >> R)
предположим наличие во внешней газовой среде градиентов концентраций
с началом в центре
частицы. На относительно большом удалении от частицы (r >> R)
предположим наличие во внешней газовой среде градиентов концентраций ![]() и
и ![]() (t – время), причем
(t – время), причем
![]() .
.
Для
определенности будем считать, что направление градиента концентрации ![]() совпадает с направлением
полярной оси. Согласно выбору начала системы координат, частицу будем считать
покоящейся, а центр инерции внешней среды движущимся относительно частицы при
совпадает с направлением
полярной оси. Согласно выбору начала системы координат, частицу будем считать
покоящейся, а центр инерции внешней среды движущимся относительно частицы при ![]() со скоростью
со скоростью ![]() . При этом модуль скорости диффузиофореза частицы
. При этом модуль скорости диффузиофореза частицы ![]() относительно центра
инерции внешней среды определяется равенством
относительно центра
инерции внешней среды определяется равенством
![]() .
.
Картина обтекания сферической частицы потоком
газа имеет азимутальную симметрию из-за выбора направления полярной оси вдоль
вектора ![]() . Поэтому рассматриваемые переменные величины не зависят от
угла
. Поэтому рассматриваемые переменные величины не зависят от
угла ![]() . Такое поле течения называется осесимметричным.
. Такое поле течения называется осесимметричным.
Дифференциальные уравнения движения вязкой
несжимаемой среды в сферических координатах при ее осесимметричном течении без
учета действия массовых сил можно представить в виде [7]
![]() ,
,
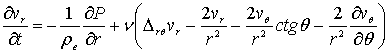 ,
,
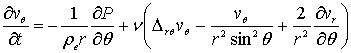 ,
,
где
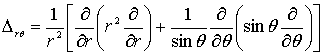 ,
,
![]() ,
, ![]() – соответственно
радиальная и касательная компоненты локальной среднемассовой скорости газовой
среды
– соответственно
радиальная и касательная компоненты локальной среднемассовой скорости газовой
среды ![]() ,
, ![]() – кинематический
коэффициент вязкости,
– кинематический
коэффициент вязкости, ![]() – плотность среды,
– плотность среды, ![]() – давление.
– давление.
На
достаточно большом расстоянии от частицы (при ![]() ) справедливы граничные условия [10]:
) справедливы граничные условия [10]:
![]() ,
,
![]() .
.
На поверхности частицы
справедливо граничное условие
![]() ,
,
показывающее, что
твердая поверхность частицы неподвижна.
Распределение
концентрации первого компонента бинарной газовой смеси удовлетворяет
дифференциальному уравнению
![]() ,
,
где ![]() – коэффициент
диффузии.
– коэффициент
диффузии.
На
поверхности частицы выполняется граничное условие:
![]() .
.
Это
условие означает, что на поверхности частицы не происходит изменения
концентрации первого компонента смеси.
При ![]() справедливо граничное
условие
справедливо граничное
условие
![]() ,
,
где 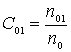 (
(![]() – среднее число молекул первого компонента газовой смеси в
единице объема,
– среднее число молекул первого компонента газовой смеси в
единице объема, ![]() – среднее число молекул газовой смеси в единице объема).
– среднее число молекул газовой смеси в единице объема).
Учет явления
диффузионного скольжения газа вдоль поверхности частицы описывается следующим
граничным условием [10]:
![]() ,
,
где ![]() – коэффициент диффузионного
скольжения.
– коэффициент диффузионного
скольжения.
При
построении теории нестационарного диффузиофореза мы предполагаем, что при
нулевом значении времени имеет место его стационарный случай, а при значениях
времени ![]() происходит наложение
строго нестационарного диффузиофореза на имеющийся стационарный процесс.
Поэтому необходимо провести разделение граничных условий для стационарного и
строго нестационарного случаев диффузиофореза.
происходит наложение
строго нестационарного диффузиофореза на имеющийся стационарный процесс.
Поэтому необходимо провести разделение граничных условий для стационарного и
строго нестационарного случаев диффузиофореза.
Для давления
полагаем
![]() ,
,
![]() ,
,
следовательно,
![]() .
.
Проведем
дальнейшее разделение граничных условий для стационарного и строго
нестационарного случаев диффузиофореза. Полагаем
![]() ,
,
![]() ,
,
причем,
![]() ,
,
![]() ,
,
следовательно,
![]() ,
,
![]() .
.
Следует считать, что
![]() ,
,
![]() ,
,
![]() .
.
Таким образом, гидродинамическая задача разбивается
на стационарную и строго нестационарную части. В результате решения стационарной части этой задачи получается условие
для определения абсолютной величины диффузиофоретической скорости частицы,
учитывающее явление диффузионного скольжения газа в стационарном случае:
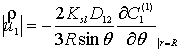 .
.
Решение строго
нестационарной части гидродинамической задачи проводится методом интегральных
преобразований Лапласа [5].
Пусть ![]() – плотность вещества
сферической частицы. Тогда при
– плотность вещества
сферической частицы. Тогда при ![]() получаем условие для
определения нестационарной составляющей диффузиофоретической скорости частицы
получаем условие для
определения нестационарной составляющей диффузиофоретической скорости частицы
![]() ,
,
где символ ![]() обозначает операцию свертывания, а
обозначает операцию свертывания, а
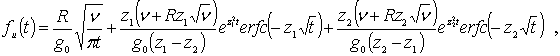
где
![]() ,
, 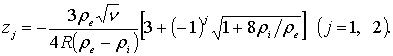
В случае ![]() получаем равенство
получаем равенство
![]() ,
,
аналогичное
равенству, имеющему место в стационарном случае диффузиофореза.
Для того, чтобы
получить окончательные формулы, описывающие зависимость стационарной и нестационарной
составляющих диффузиофоретической скорости сферической частицы от
соответствующих слагаемых градиента концентрации, необходимо решить надлежащую диффузионную
задачу и определить выражения
![]() ,
, ![]() .
.
Литература
1. Баринова М. Ф., Костицына Л. И., Яламов
Ю.И. Теория движения твердой сферической частицы в неоднородной вязкой среде. –
М.: Издательство МГОУ, 2005. – 120 с.
2.
Бейтмен Г., Эрдейи А. Таблицы интегральных преобразований. Т. 1. – М.: Наука,
1969. – 344 с.
3.
Деч Г. Руководство к практическому применению преобразования Лапласа и
Z-преобразования. – М.: Наука, 1971. – 288 с.
4.
Коренев Б. Г. Введение в теорию бесселевых функций. – М.: Наука, 1971. – 288 с.
5.
Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. –
СПб.: Лань, 2002. – 688 с.
6.
Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. Т. 6. Гидродинамика. – М.:
ФИЗМАТЛИТ, 2006. – 736 с.
7.
Слезкин Н. А. Динамика вязкой несжимаемой жидкости. – М.: Гостехиздат, 1955. –
520 с.
8.
Тихонов А. Н., Самарский А. А. Уравнения математической физики. – М.:
Издательство МГУ, Наука, 2004. – 798 с.
9.
Фукс Н. А. Механика аэрозолей. – М.: Издательство АН СССР, 1955. – 352 с.
10.
Яламов Ю. И., Галоян В. С. Динамика капель в неоднородных вязких средах. –
Ереван: Луйс, 1985. – 208 с.
11. Янке Е., Эмде Ф.,
Леш Ф. Специальные функции. – М.: Наука, 1968. – 344 с.