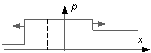Васильева О.В.

Национальный Исследовательский Томский политехнический университет, Россия

Моделирование движения газовой волны и апробация алгоритма в точке торможения в коаксиальном магнитоплазменном ускорителе

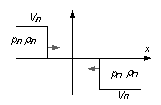
При вылете плазменной субстанции из ствола коаксиального магнитоплазменного ускорителя [1], перед ее головной частью образуется отсоединенная ударная волна. Разработаем алгоритм расчета термодинамических параметров и апробируем его в точке торможения за ударной волной. Для этого примем некоторые упрощения – субстанцию условно будем называть затупленным телом или поршнем, расчет будем производить в одномерном случае. Если перейти к системе координат, связанной с поршнем, тогда невозмущенный газ-воздух будет двигаться на поршень со скоростью поршня.

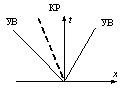
При моделировании движения газовой волны на твердую преграду модель можно заменить другой эквивалентной моделью - движением двух одинаковых волн на встречу друг другу. Приведем схему этой задачи называемой нестационарным газодинамическим разрывом. Схематически картину течения можно изобразить в виде конфигурации представленной в Тб. 1 [2, 3]. Конфигурация содержат контактный разрыв (КР), на котором имеет место разрыв плотности , а давление и скорость остаются непрерывными (см. Тб. 1). Для решения одномерной нестационарной газодинамической задачи будем использовать уравнения сохранения массы, импульса и энергии, записанные в дивергентной форме (1).

Здесь - плотность газа, - давление газа, - скорость распространения газа, - внутренняя энергия газа, - время и координата соответственно.

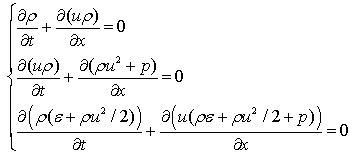(1)

Табл. 1. Конфигурации нестационарного газодинамического разрыва

Схематическое изображение	Комментарии
	Случай наблюдается при столкновении двух масс газа, движущихся навстречу друг другу. График характеристики волн: УВ – ударная волна; КР – контактный разрыв (пунктир линия – скачек плотности ρ). На границе раздела – контактном разрыве не может быть скачек давления p. На границе раздела – контактном разрыве не может быть скачек скорости v.

Результат расчета динамики изменения термодинамических параметров в относительных единицах приведен ниже на рисунке 1 (случай двух ударных волн). До столкновения волн величины давления плотности и температуры в средах были одинаковы, а скорости волн одинаковые по величине, но разные по направлению (знаку). На рисунке приведен момент времени после столкновения двух ударных волн, при числе Маха равном 1,5. Осью симметрии рисунков является фронт плазменного поршня.

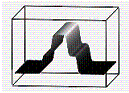
а б в г

а - плотность ; б - давление ; в - скорость ; г - энергия

Рис. 1. Моделирование движения газовой волны

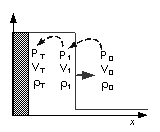
Рис. 2. Критические параметры ударной волны

Для численного решения системы уравнений (1) использовался модифицированный алгоритм Лакса–Уэндроффа. Подробная программная реализация алгоритма представлена в [3].

Проверка работы алгоритма была проведена на расчете критических параметров в точке торможения – давление торможения , плотность торможения и температура торможения (см. рис. 2), при заданных начальных данных невозмущенного газа (в относительных единицах), - показатель политропы и заданном числе Маха . Давление, плотность и температура из невозмущенной среды, через скачок уплотнения, пересчитываются через ударную адиабату Гюгонио-Ренкина [3].

В нашем случае эти формулы вырождаются в простые удобные для инженерных расчетов соотношения:

, ,   .

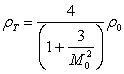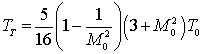Для расчета параметров торможения нужно использовать адиабату Пуассона: , ,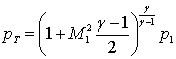

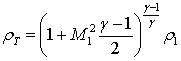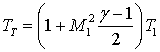
Здесь - числа Маха после ударной волны. Для инженерных расчетов получаем: ,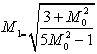

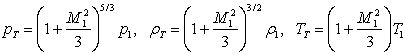
Начальные данные приведены к относительным единицам .

Результаты сравнения методов сведем в табл. 2.

Таблица 2. Результаты сравнения инженерного (И) и программного (П) расчетов

Число Маха M0							Расчет
1,5	1,536	2,280	1,714	2,172	1,495	1,750	И
	1,542	2,287	1,717	2,175	1,497	1,752	П
2	2,850	3,807	2,286	2,719	2,078	2,333	И
	2,914	3,893	2,306	2,744	2,106	2,364	П
3	6,600	8,204	3,000	3,418	3,667	4,000	И
	6,557	8,151	2,995	3,413	3,649	3,980	П
5	18,600	22,300	3,571	3,982	8,680	9,333	И
	18,522	22,206	3,570	3,980	8,647	9,298	П
10	74,850	88,397	3,883	4,291	32,123	34,333	И
	75,050	88,643	3,884	4,291	32,210	34,426	П

В работе смоделировано движение газовой волны на твердую преграду, проведена апробация алгоритма, разработанного на основе модифицированного алгоритма Лакса–Уэндроффа [3], в точке торможения за ударной волной. Результат расчета газодинамических параметров в точке торможения совпадает с литературными данными.

Литература

1. Сивков А.А., Герасимов Д.Ю., Цыбина А.С. Электроэрозийная наработка материала в коаксиальном магнитоплазменном ускорителе для нанесения покрытий // Электротехника. – Томск, 2005. – №.6.– С.25 – 38.

2. Морозов А.И. Введение в плазмодинамику. – М.: ФИЗМАТЛИТ, 2008, – 613 с.

3. Сивков А. А., Исаев Ю. Н., Васильева О.В. Купцов А. М. Моделирование газодинамических процессов и оценка термодинамических параметров ударной волны плазменного газа коаксиального магнитоплазменного ускорителя // Известия Томского политехнического университета. – Томск, 2012. - Т. 320 - №. 2. - C. 53-58.