Д. ф.-м. н. Белов В. Т.

КЭИ ГВУЗ КНЭУ им. В. Гетьмана, Украина

ЧАСТНАЯ ТЕРМОДИНАМИЧЕСКАЯ СИСТЕМА И ЕЕ ТЕРМОДИНАМИЧЕСКИЕ ПАРАМЕТРЫ.

Введение.

На зрелой стадии своего развития любая теория аксиоматизируется, т. е. появляется система аксиом и связанных с ней первичных понятий этой теории, из которых строго логическим путем доказываются те или иные следствия этой теории. Не избежала аксиоматизации и термодинамика, в которой за продолжительное время появилась своя система аксиом – I, II и III начала термодинамики.

Вводимая в теории (термодинамике) система аксиом всегда должна удовлетворять следующим требованиям: быть полной, независимой и непротиворечивой. Система аксиом считается полной, если нельзя выдвинуть такое предположение, которое может быть получено из системы аксиом правильными логическими рассуждениями. Система аксиом считается независимой, если никакая из аксиом данной теории не может быть получена из остальных как логическое следствие. Система аксиом считается непротиворечивой, если из нее нельзя правильными рассуждениями вывести два следствия, логически исключающие друг друга.

При создании любой системы аксиом и связанной с ней системы первичных понятий важнейшим аспектом является проблема внешнего оправдания вводимой системы аксиом и первичных понятий. Под проблемой внешнего оправдания системы аксиом будем понимать логически строгое соответствие всех следствий из системы аксиом всем экспериментальным фактам, взятым из природы, и всем выводам, вытекающим из науки. Поэтому все теории, созданные человеческим разумом, можно разделить на научные теории, требующие внешнего оправдания, и религии, не требующие внешнего оправдания.

Особенностью термодинамики как аксиоматической теории является то, что каждая из ее аксиом была выдвинута в разное время разными учеными. Поэтому в термодинамике за прошедшие триста лет сохранилось множество мелких правил, законов, уравнений, рецептов и т. д., введенных без должного внешнего оправдания. Все это множество аксиоматически введенных правил, понятий и утверждений, очевидно, представляет собой «строительные леса», примененные при создании термодинамики как аксиоматической теории. Совершенно ясно, что при построении строгой аксиоматической теории эти «строительные леса» необходимо убрать. Понятно, что определение того, что именно является «строительными лесами» дается самой системой аксиом, которая, слава Богу, имеется в термодинамике.

Следующей особенностью термодинамики как аксиоматической теории, является то, что термодинамика со своими аксиомами и системой первичных и вторичных понятий тесно связана с аксиоматической системой классической механики. Поэтому I начало термодинамики является следствием закона сохранения энергии, а многие понятия механики, такие как работа, сила, давление, объем, время, пространство и т. д. широко используются и в термодинамике. Проблема внешнего оправдания системы аксиом термодинамики строго требует, чтобы все механические понятия, используемые в термодинамике, обязательно имели тот же физический и математический смыслы, как и в механике. Таким образом, если давление в механике и в математике является векторной величиной, то и в термодинамике давление газа, жидкости, твердого тела должно также быть векторной величиной; если в механике имеется кинетическая энергия, потенциальная энергия и полная механическая энергия, причем потенциальная энергия притяжения отрицательна, а потенциальная энергия отталкивания положительна, то и потенциальная энергия притяжения атомов или молекул в жидкости, газе и твердом теле также должна быть отрицательной. Итак, аксиоматизация любой научной теории требует четкого единообразия используемых понятий, так как без этого нет собственно и аксиоматической теории.

Так как термодинамика является количественной наукой, то проблема внешнего оправдания вводимой системы аксиом требует, чтобы все количественные понятия и качественные математические понятия в термодинамике полностью удовлетворялись бы математикой, понимаемой как весь спектр математических дисциплин. Совершенно ясно, что если вследствие исторических причин имеется разночтение между термодинамикой и математикой, то это обязательно должно оговариваться.

Из вышеизложенного следует, что основной целью этого цикла статей является уточнение системы аксиом термодинамики и уборка «строительных лесов» оставшихся в ней в силу тех или иных исторических причин.

ПЕРВИЧНЫЕ ФИЗИЧЕСКИЕ ПОНЯТИЯ ТЕРМОДИНАМИКИ.

Любая физическая аксиоматическая теория всегда содержит систему первоначальных физических понятий этой теории. Термодинамику, основанную на трех началах термодинамики как аксиомах, отличает то, что большое количество первоначальных термодинамических понятий было взято из классической механики. Так как наука представляет собой систему взаимосвязанных понятий, то ясно, что вводимые термодинамические понятия как понятия вторичные должны учитывать имеющиеся первичные механические понятия и должны быть согласованы с уже имеющимися математическими понятиями, на основе которых правильным логическим способом вводится количественное описание термодинамики.

Все физические понятия по отношению к окружающему нас материальному миру можно разделить на две принципиально разные группы: физические объекты и способы физического описания. Те физические понятия, которым в материальном мире соответствуют конкретные материальные тела, и будем называть физическими объектами, т. е. атом или молекула – это физический объект. Те же физические понятия, которым в материальном мире не соответствуют какие-либо конкретные материальные тела, будем называть способами физического описания, т. е. физическое понятие «траектория» по которой движется атом или молекула является способом физического описания: никто не принесет «куска траектории», так как это воображаемая пространственная кривая, по которой движется атом или молекула.

Дополнительно, все физические понятия можно подразделить на измеряемые и неизмеряемые. Например, нельзя сказать, что атом азота «атомнее» атома гелия, так как физическое качество «атомность» не измеримо в силу своего определения. В то же время понятие «траектория» является измеримым и можно говорить о длине траектории.

Подробное рассмотрение этих методических вопросов необходимо в силу того, что в широко распространенной литературе по физике существует масса ошибок и разногласий по этим вопросам. Будем, однако, считать, что если в литературе и в данной статье выражено одинаковое понимание термодинамических понятий, то автоматически принимается определение таких термодинамических понятий, и далее используем эти понятия без их определения, чтобы не загромождать статью.

Любая термодинамическая система изменяется и развивается во времени и в пространстве: Л. Больцман говорил о термодинамической стреле времени. Поэтому введем понятие «пространства» и понятие «времени».

Пространство – это способ, которым человек представляет взаимное расположение окружающих его физических объектов, существующих независимо от его сознания. Критикам такого определения дадим задание принести «кусок пространства» или «атома пространства». До получения материальных подтверждений материальности пространства и наличия материального атома пространства спокойно можно обойтись этим определением. Таким образом, пространство – это человеческое понятие и в силу этого по историческим причинам понятие «пространства» развивается со временем.

Временем назовем способ, которым человек характеризует существующую в природе, независимо от человека необратимость всех природных процессов. Для количественного описания времени можно использовать как периодические процессы (часы), так и необратимые процессы (радиоактивный распад). Учитывая все неудачные экспериментальные попытки доказать «материальность времени» и наличие «атомов времени» время также является способом физического описания.

Любая термодинамическая система состоит из совокупности частиц, различающихся массой, зарядом и т. д. и взаимодействующих между собой по различным законам. Представляется логичным с целью упрощения количественного описания термодинамики выделить среди всех возможных термодинамических систем такие системы, которые нельзя дальше упрощать и которые имеют для всех частиц одинаковые физические характеристики. Тогда частной термодинамической системой (ЧТС) назовем совокупность одинаковых по всем физическим характеристикам частиц, взаимодействующих между собой по одному и тому же закону. Такое определение ЧТС позволяет учесть даже наличие изотопов у химических элементов: обычная вода и тяжелая вода представляют собой различные ЧТС, имеющие различные термодинамические характеристики: точку замерзания, точку кипения и т. д. В то же время, любую реальную термодинамическую систему можно рассматривать как результат взаимодействия нескольких ЧТС, существующих в одном объеме.

Любая термодинамическая система, в том числе и ЧТС, имеет энергию. Энергию, заключенную в термодинамической системе или в ЧТС принято называть внутренней энергией . В классической механике энергию принято подразделять на кинетическую и потенциальную энергию, причем принято считать кинетическую энергию и потенциальную энергию отталкивания положительной величиной, а потенциальную энергию притяжения отрицательной величиной. Для описания совокупности движущихся и взаимодействующих по какому-то закону частиц в классической и квантовой механике вводится понятие полной механической энергии: как алгебраической суммы кинетической и потенциальной энергий. Причем, полная механическая энергия в любой термодинамической системе или в ЧТС может принимать как положительные, так и отрицательные значения. При отрицательном значении полной механической энергии термодинамическая система или ЧТС и совокупность составляющих ее частиц находится в связанном состоянии: траектории всех частиц в совокупности финитны и частицы не могут покидать определенный объем. Объемом назовем часть пространства, в котором размещена термодинамическая система или ЧТС.

Основное принципиальное отличие термодинамических систем и ЧТС от механических и квантово-механических систем заключается в том, что в термодинамических системах всегда необходимо существует тепловое излучение, т. е. газ фотонов. Естественно, что энергию электромагнитного излучения необходимо включить в состав внутренней энергии термодинамической системы. Итак, внутренней энергией частной термодинамической системы назовем алгебраическую сумму кинетической, потенциальной и электромагнитной энергий, имеющихся в термодинамической системе, т. е.

………………………………..(1)

где: К – кинетическая энергия; П – потенциальная энергия; Е – энергия электромагнитного излучения, содержащаяся в ЧТС. Согласно (1) внутренняя энергия ЧТС может принимать как положительные, так и отрицательные значения.

Так как ЧТС, как и любая термодинамическая система состоит из очень большой совокупности частиц, то для нее можно ввести статистическую математическую характеристику: среднее значение внутренней энергии, приходящейся на одну частицу. Исторически сложилось так, что среднее значение принято измерять в . Тогда, собственной температурой частной термодинамической системы назовем среднюю внутреннюю энергию ЧТС одной частицы, измеренную в кельвинах, т. е.

…………….или …………..(2)

где: - постоянная Больцмана.

Естественно, что может принимать как положительные, так и отрицательные значения, как это показано на рис. 1.

Рис. 1. Шкала собственной температуры

Отметим, что отрицательные значения не имеют ничего общего с отрицательной абсолютной температурой, которая описана в [1]. Абсолютная отрицательная температура вводится на примере системы ядерных спинов некоторых кристаллов, например . Температура соответствует состоянию, в котором все спины ориентированы в направлении внешнего магнитного поля В, температура (или ) – состоянию полной хаотичности в ориентации спинов, температура - состоянию, при котором все спины ориентированы в направлении, противоположном внешнему магнитному полю В. Условием появления отрицательных абсолютных температур служит .

Система ядерных спинов согласно определению представляет собой частную термодинамическую систему, в которой преобладает закон магнитного взаимодействия спинов во внешнем магнитном поле В. Внутренняя энергия системы спинов состоит только из потенциальной энергии взаимодействия спинов и для системы из спинов имеем:

………………….(3)

Так как при , то условие появления отрицательных абсолютных температур не выполняется. Для собственной же температуры ЧТС имеем такое выражение:

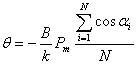……………………………………(4)

Причем и , а не как полагается в [1]. Итак, собственная температура позволяет описать и такие экзотические ЧТС как система ядерных спинов.

Введение любой физической системы отсчета, в частности температурной шкалы, требует наличия как минимум двух реально существующих физических тел: тела отсчета, относительно которого замечается тепловое движение, и тела, которое совершает тепловое движение. В отличие от механики, где состав тела отсчета не играет никакой роли, в термодинамике состав тела отсчета играет принципиальную роль. При выборе тела отсчета (термометрического тела) возможны два варианта: в первом случае термометрическое тело имеет тот же состав, что и данная ЧТС, тепловое движение которой исследуется, а во втором случае термометрическое тело имеет другой состав, чем заданная ЧТС. В термодинамике в настоящее время реализован второй подход, в котором в качестве универсального термометрического тела используется идеальный газ и введена абсолютная температурная шкала. Недостатком существующего подхода является невозможность с помощью этой абсолютной температурной шкалы описать тепловое движение в жидкости и в твердом теле.

В случае же когда термометрическое тело имеет тот же состав, что и исследуемая ЧТС, эмпирической основой для такой температурной шкалы является эмпирический закон соответственных состояний [1], когда за ноль отсчета температурной шкалы принимается критическая температура жидкости . Известно, что различные ЧТС имеют различные критические температуры в абсолютной температурной шкале и если совместить критические температуры различных ЧТС, то получим единую температурную шкалу, в которой твердое, жидкое и газообразное состояние ЧТС будет описываться одинаковой температурой, как это показано на рис. 2:

Рис. 2. Совмещение некоторых ЧТС с нулем идеального газа

Таким образом, согласно закону соответственных состояний одинаковая температура для любой ЧТС должна будет описывать одинаковое физическое состояние (газ, жидкость или твердое тело). Эта одинаковая для всех ЧТС температура, введенная аксиоматическим путем и названная ранее собственной температурой , имеет солидное эмпирическое обоснование и должна выглядеть, как показано на рис. 3.

Рис. 3. Привязка аксиоматической собственной температуры к эмпирической шкале состояний ЧТС.

Аксиоматический путь введения собственной температуры ЧТС не является единственно возможным. Действительно, так как давление и объем , как первичные понятия определены в механике, то, используя уравнение состояния реального термометрического тела , можно из него выразить температуру как функцию от и , которые можно определить экспериментально. К сожалению, при таком аксиоматическом определении температуры в результате наличия у реальных термометрических тел разных уравнений состояния (которых имеется в литературе более двухсот), при одинаковых значениях и получим множество разных значений температуры: ; ;……; . Какая из полученных расчетных значений абсолютных температур , , является истинной непонятно. Таким образом, при эмпирическом определении температуры как параметра термодинамической системы существует проблема множественности уравнений состояния и соответственно множественности абсолютных температур.

Дальнейшие вопросы, связанные с введением единой шкалы собственной температуры будут рассмотрены в последующих статьях по мере их логического следования.

Следующим термодинамическим параметром ЧТС является ее собственное давление . Практически во всей физической литературе и соответственно в [1] давление определяется как абсолютная величина силы, действующая на единицу поверхности, нормально к этой поверхности. Такое определение давления является ошибочным, так как игнорирует векторный характер силы и тип поверхности, к которой проводится нормаль . Дадим аксиоматическое определение собственного давления , основанное на математическом определении поверхности [2].

Собственное давление ЧТС определим как силу , действующую на элементарную площадку нормально к поверхности . Так как по правилам действия с векторными величинами при таком определении собственное давление является векторной величиной, то дадим физическую интерпретацию отрицательного и положительного давлений ЧТС. Согласно математическим правилам положительным является вектор , направленный по оси Х, а отрицательным является вектор , направленный против оси, так как это показано на рис. 4.

Рис. 4. Направление вектора силы

С физической точки зрения разные направления силы или что тоже вектора собственного давления можно интерпретировать так: рассмотрим пружину «а», находящуюся в свободном состоянии, как это показано на рис. 5а. Если теперь приложить к ней силу , растягивающую эту пружину, так как это показано на рис. 5б, то в силу исторических причин эту силу будем считать положительной. Если же теперь к пружине приложить силу , сжимающую пружину, так как это показано на рис. 5, то эту силу будем считать отрицательной. Как известно, такая интерпретация полностью соответствует требованиям математики.

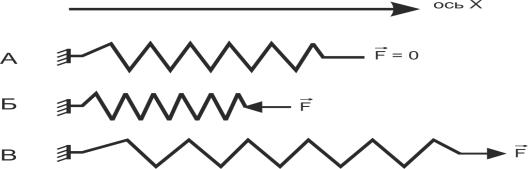
Рис. 5. Физическая интерпретация направления силы

Для определения собственного давления ЧТС, рассмотрим теперь конкретную поверхность , отделяющую жидкость от газа. Согласно [2] все поверхности в математике принято классифицировать на односторонние, двухсторонние гладкие и кусочно-гладкие двухсторонние поверхности. С точки зрения наглядности одностороннюю поверхность можно определить как такую поверхность, которую можно полностью покрасить, не пробивая поверхность, например, лист Мебиуса [2]. Гладкой двухсторонней поверхностью для наглядности назовем такую поверхность, которую можно покрасить полностью, только пробив эту поверхность. И с наглядной точки зрения и со строго математической точки зрения [2] поверхность , отделяющая жидкость от газа, является двухсторонней поверхностью, что и показано на рис. 6. Твердое тело в равновесном состоянии является монокристаллом и поверхность монокристалла согласно [2] представляет собой кусочно-гладкую двухстороннюю поверхность . Согласно [2] к каждой точке двухсторонней поверхности можно провести четыре направления нормали : , - показанные для наглядности в разных точках поверхности .

Рис. 6. Двухсторонняя поверхность жидкость – газ, твердое тело - газ.

В математике, используя понятие ориентации поверхности относительно системы пространственных координат , вводят понятие ориентации пространства. Согласно [2] будем всегда предполагать правую ориентацию пространства, когда оси координат располагаются так, что вращение от оси Х к оси Y кажется происходящим против часовой стрелки, если на них смотреть из конца положительной оси Z. Отметим, что правая ориентация пространства обязательно предполагает правую координатную систему. Так как жидкость и твердое тело всегда представляет замкнутое тело, то у них необходимо выделить внешнюю и внутреннюю относительно этого замкнутого тела стороны этой поверхности .

В физике, в отличие от математики, в силу исторических причин, положительным считается направление нормали , так как давление газа принимается за положительное и это газовое давление растягивает ограничивающую поверхность , так же как и сила в рис. 5б растягивает пружину. Таким образом, собственное давление будет положительным, т. е. + . Экспериментально известно, что в жидкости и твердом теле силы притяжения направлены внутрь и сжимают внутреннюю сторону поверхности , уменьшая ее величину. Таким образом, собственное давление в жидкости и твердом теле имеет отрицательный характер, т. е. - , что соответствует направлению нормали . Итак, со строгой математической точки зрения с учетом исторических причин собственное давление в жидкости и твердом теле будет отрицательным, а собственное давление в газе будет положительным.

Дальнейшее рассмотрение других собственных термодинамических параметров ЧТС возможно только на основе I, II, III начал термодинамики, так как эти термодинамические параметры являются вторичными по сравнению с объемом, собственной температурой и собственным давлением.

Литература

1. Ландау Л. Д., Лившиц Е. М., Статистическая физика, Ч. 1., Наука, 1976 г., с. 584.

2. Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, Т. 3., М., Физматгиз, 1960 г., с. 656.