Д. ф.-м. н. Белов В. Т.

КЭИ ГВУЗ КНЭУ им. В. Гетьмана, Украина

 

УРАВНЕНИЕ СОСТОЯНИЯ РЕАЛЬНОГО ГАЗА

 

Одним из важнейших понятий молекулярно-кинетической теории газов и технической термодинамики является уравнение состояния важнейших технических газов. Уравнением состояния назовем уравнение , связывающее термодинамические параметры газа. Основным требованием со стороны фундаментальной физики к уравнению  состояния реального газа является то, что оно всегда должно удовлетворять I и II началам термодинамики.

В настоящее время в литературе приведены более двухсот уравнений состояния технически важных газов. К сожалению, авторы этих уравнений состояния все внимание обращали на соответствие этих уравнений эмпирическим данным, а не на их соответствие I и II началам термодинамики. Естественно, что несоблюдение данным уравнением состояния реального газа хотя бы одного из начал термодинамики ставит крест на нем, какие бы теоретические или экспериментальные соображения не приводились бы в его пользу. Между тем, уравнение состояния идеального газа полностью удовлетворяет I и II началам термодинамики, что позволяет методом сравнения сделать выводы о соблюдении I и II начал термодинамики также тем или иным уравнением состояния реального газа.

В молекулярной физике в учебных пособиях широко освещается уравнение состояния реального газа Ван-Дер-Ваальса, иллюстрирующее те или иные аспекты теории реальных газов и жидкости, а также фазовых переходов между ними. Так как уравнение Ван-Дер-Ваальса является простейшим из предложенных уравнений состояния реальных газов, то ясно, что сравнение необходимо начать с него, а потом из этого конкретного случая можно сделать некоторые общие выводы относительно других более сложных уравнений состояния. Так как все равно, нарушение какого из начал термодинамики рассматривать, то выгодно использовать II начало термодинамики, имеющее количественную форму  в принятых в [1] обозначениях.

Таким образом, настоящая работа посвящена тому, как, используя II начало термодинамики, проверить существующие уравнения состояния реальных газов и получить уравнение состояния реального газа, точно удовлетворяющее I и II началам термодинамики.

Рассмотрим 1 моль идеального газа и проведем с ним следующий термодинамический цикл, состоящий из четырех обратимых процессов: изотермического расширения 1-2 при температуре ; изохорического охлаждения 2-3 при ; изотермического сжатия 3-4 при температуре  и изохорического нагрева 4-1 при . Этот цикл показан на рис. 1 и используя известные формулы процессов идеального газа, можно рассчитать термический к.п.д. такого цикла равный , т. е. он равен к.п.д. цикла Карно.

 

 

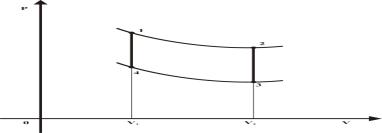
Рис. 1. Термодинамический цикл (12341).

 

 

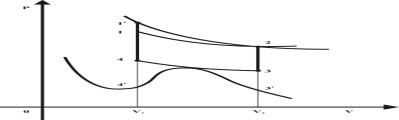
Рис. 2. Термодинамический цикл для газа Ван-дер-Ваальса

Возьмем теперь один моль реального газа, уравнение состояния которого удовлетворяет формуле Ван-Дер-Ваальса  в принятых в [1] обозначениях. Выберем температуру изотермы  достаточно большой, чтобы процесс изотермического расширения , показанный на рис. 2., прошел через точку 2, точку пересечения изотермы  идеального газа и изотермы  газа Ван-Дер-Ваальса. Это всегда возможно, так как уравнение изотермы Ван-Дер-Ваальса представляет собой уравнение третьей степени от [1], а, согласно аналитической геометрии, уравнение первой степени от  и уравнение третьей степени от всегда имеют хотя бы одну точку пересечения.

Выберем теперь температуру  изотермического сжатия настолько низкой, чтобы изотерма газа Ван-Дер-Ваальса изобразилась характерной извилистой кривой  [1], такой, что точка пересечения этих двух изотерм находилась за пределами изохоры , так как показано на рис. 2. В итоге получим такой же термодинамический цикл: изотермическое расширение  при ; изохорического охлаждения ; изотермического сжатия  при  и изохорического нагрева . Для сравнения на рис. 2 показан такой же цикл идеального газа, у которого имеется общая точка 2 для сравнения этих циклов. Как известно, площадь любого цикла представляет собой полезную работу А и из рис. 2 следует, что полезная работа цикла идеального газа  меньше полезной работы  цикла газа Ван-Дер-Ваальса, т. е. при одинаковых температурах нагревателя  и холодильника термический к.п.д. газа Ван-Дер-Ваальса больше к.п.д. цикла Карно:

                                                   (1)

Итак, газ Ван-Дер-Ваальса нарушает II начало термодинамики и позволяет создать вечный двигатель второго рода.

Правдоподобные эмпирические и теоретические соображения дали Ван-Дер-Ваальсу возможность получить уравнение состояния реального газа и именно за него получить Нобелевскую премию по физике: неисповедимы пути твои Господи.

Рассмотрим теперь более сложные уравнения состояния, из которых особо можно выделить вириальное уравнение состояния [1-4], о котором в [3] указано, что оно является «истинным». Это вириальное уравнение состояния может быть записано в двух формах: для теоретических исследований в такой форме в принятых в [1] обозначениях, как разложение давления по степеням :

……………….(2)                            

 

где:  - термодинамические параметры; - число частиц в ограниченном объеме газа; - так называемые вириальные коэффициенты.

И для практического применения и составления таблиц в другой форме, связанной с (2):

                                                  (2а)

где:  - плотность газа;  - пересчитанные вириальные коэффициенты.

Рассмотрим теперь вопрос о том, удовлетворяет ли вириальное уравнение состояния II началу термодинамики. Доказательство ошибочности уравнения состояния Ван-Дер-Ваальса основывается на пересечения изотермы газа Ван-Дер-Ваальса и изотермы идеального газа. Из математики известно, что две кривые могут быть параллельны, если они имеют одинаковую форму математической записи и пропорциональность коэффициентов уравнений этих кривых. Таким образом, параллельной кривой уравнения идеального газа может быть только кривая, в которой уравнение имеет термодинамические параметры  только в первой степени, например, как уравнение идеального газа, Таким образом, вириальное уравнение состояния, как имеющее квадратичные, кубические и т. д. члены, должно нарушать II начало термодинамики.

Возьмем один моль реального газа, удовлетворяющего вириальному уравнению состояния (2) или (2а). Представим уравнение (2) или (2а) в виде уравнения -степени относительно объема в таком виде:

 ………………… (3)

где:  - коэффициенты, зависящие от .

 Для этого учтем в бесконечном ряде (2) или (2а) необходимое число членов уравнения (2), дающих отброшенную погрешность меньше экспериментальной ошибки определения эмпирических коэффициентов разложения по объему  . На диаграмме возьмем такую высокую температуру , чтобы изотерма идеального газа  и изотерма вириального газа  имели бы всего одну точку пересечения, так как показано на рис. 3. Выберем теперь настолько низкую температуру , чтобы уравнение (3) имело  действительных корней ,,…,и соответствующая изотерма  вириального уравнения состояния должна представлять участок кривой, как это показано на рис. 3. Отметим, что при  число корней уравнения также равно бесконечности и изотерма вириального уравнения состояния должна представлять участок горизонтальной прямой как это показано на рис. 3. Тогда, взяв точку пересечения изотерм 2 можно получить такой же термодинамический цикл, как и на рис. 2.

 

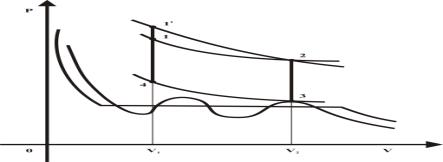
Рис. 3. Термодинамический цикл для вириального уравнения состояния газа

 

Таким образом, доказано, что и вириальное уравнение состояния нарушает II начало термодинамики. Хотя ошибочность вириального уравнения состояния доказана, однако как следует из [2-4], при эмпирическом определении параметров вириального уравнения оно достаточно точно отражает имеющиеся в [2-4] эмпирические данные. Этот факт доказывает, что вириальное уравнение состояния содержит в себе некое рациональное зерно и поэтому необходимо рассмотреть как достоинства, так и недостатки этого уравнения состояния.

В первую очередь вызывает сомнение математическая форма вириального уравнения состояния в виде степенного ряда (2) или (2а). Действительно, уже при  кг/м3 и ряд (2) и ряд (2а) расходятся и в связи с их расходимостью возникают различные физические и математические проблемы, которые рассмотрены в [5].

Следующим негативным моментом в вириальном уравнении состояния является то, что коэффициенты вириального уравнения состояния не совпадают с соответствующими коэффициентами степенного ряда, т.е. вириальное уравнение состояния нельзя трактовать как разложение какой-либо функции [5]. Отметим, как недостаток и то, что на практике [2-5] всегда предпочитают экспериментальное определение вириальных коэффициентов методом наименьших квадратов.

Фундаментальным же физическим недостатком вириальных уравнений состояния (2) и (2а) является то, что в любом объеме реального газа вне зависимости от сочетания термодинамических параметров всегда в термодинамической системе содержится одинаковое число частиц, т. е. . Согласно же имеющимся экспериментальным данным [2-5] в реальном газе всегда имеются ассоциации молекул или атомов, число которых меняется в зависимости от изменения термодинамических параметров. Наиболее сильно этот эффект выявляется в реальном газе при критических условиях [2-4], что и показывает табл. 1.

 

Таблица 1.

Среднее число атомов или молекул в ассоциации

№

Газ

Критические параметры

, Кг/

кмоль

Среднее число атомов или молекул в ассоциации

,  

, МПа

, Кг/м3

1

Гелий,

5,2

0,226

64

4,003

3,08

2

Неон,

44,4

2,62

484

20,18

3,24

3

Аргон,

150,65

4,8

531

39,95

3,47

4

Криптон,

209,39

5,42

908

83,8

3,48

5

Ксенон,

289,74

5,75

1155

131,3

3,56

6

Азот,

126,25

3,354

311

28,02

3,47

7

Кислород,

154,78

5,014

410

32

3,29

8

Окись углерода,

132,91

3,453

301

28,01

3,44

9

Водород,

33

1,28

32

2,016

3,40

10

Хлор,

417,15

7,61

573

70,90

3,68

11

Вода,

647,2

22,11

324

18,016

4,38

12

Углекислота,

304,19

7,285

468

44,01

3,69

13

Аммиак,

405,6

11,3

235

18,032

3,89

14

Гексафторид серы,

318,7

3,711

751

146,06

3,67

 

Среднее число атомов или молекул  в ассоциации рассчитывается по формуле , где эффективная молярная масса определяется из уравнения идеального газа по эмпирическим данным по формуле . Из данных таблицы 1 следует, что наличие ассоциаций играет решающую роль в уравнении состояния реального газа.

Итак, с позиций критики [5] можно не без оснований утверждать, что вириальное уравнение состояния есть больше акт полной безнадежности, чем изящное выражение строгого физического закона.

После этого вывода [5] возникает вопрос о том, каким же уравнением состояния необходимо заменить вириальное уравнение состояния, чтобы исключить все его недостатки. Наводящее соображение к этой дилемме дает эмпирическое уравнение состояния реального газа (2а): эмпирически определяемая величина имеет размерность равную [моль] и поэтому  необходимо разлагать в ряд по числу молей, а не по плотности, как это сделано в (2а). Такое разложение можно получить следующим способом.

Пусть имеется реальный газ с молярной массой  и массой . Наличие ассоциаций в таком реальном газе можно представить как смесь различных идеальных газов с молярными массами , 2, 3…, п0, где п0 – максимальное число атомов или молекул в ассоциации, причем п0   - общего числа атомов реального газа массой . Таким образом, ассоциации необходимо рассматривать именно как различные идеальные газы с соответствующими молярными массами. Тогда, для парциальных давлений этих идеальных газов по закону Дальтона можно записать следующие формулы:

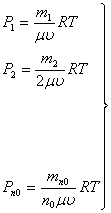  …………………………………………….(4)

 

где: , ,… - массы идеальных газов с молярными массами , 2, ,…, ; - объем газа; абсолютная температура.

По закону сохранения энергии получим, что

 ………………………………. (5)

Обозначив  и произведя преобразования получим:

 ……………………………………..(5а)

Далее используя, что  - числу молей газа из (5а) можно получить такое разложение по молям:

  ………………………………………….(6)

Полученное разложение по молям различных ассоциаций идеальных газов полностью удовлетворяет все требования к уравнению состояния вириального типа: оно не расходится, так как масса  реального газа конечна и конечно число возможных ассоциаций; имеет одинаковую размерность с известным эмпирическим разложением (2а), т. е. при эмпирическом определении числа молей методом наименьших квадратов дает такие же абсолютные  расчетные ошибки как [2-5], так как использует те же эмпирические данные; полученное разложение имеет самый фундаментальный характер.

Учитывая, что + +…..+= - общей массе реального газа, введем понятие эффективной молярной массы  и запишем уравнение реального газа в привычной форме:

  .……………………………………………………….(7)

где:

Уравнение реального газа в форме (7) вполне удовлетворяет II началу термодинамики. Действительно, подставив (7) в формулу термического к.п.д. для термодинамического цикла из двух изотерм и двух изохор получим:

 …………(8)

Уравнение реального и идеального газов в форме (7) позволяет создать единую шкалу термодинамической температуры и решить логическое противоречие, отмеченное в [6].

В термодинамике имеется понятие обратимого и необратимого термодинамического процесса. Уравнение (5а) позволяет количественно определить отличие обратимого процесса от необратимого. Тогда, термодинамический процесс будет обратимым, если отношение  в уравнении (5а) при  и термодинамический процесс будет необратимым, если .

Полученное уравнение состояния реального газа ставит необходимость его тщательной проверки по имеющимся эмпирическим данным широко разбросанным по соответствующим источникам в литературе. Ввиду большого обилия имеющегося для обработки материала целесообразно разместить его в отдельных статьях с учетом химической структуры атомов и молекул реального газа.

Следующим важным выводом из методики получения уравнения состояния является вывод о том, что согласно II начала термодинамики, любое уравнение состояния любого вещества в любой фазе должно быть комбинацией термодинамических параметров в первой степени. Этот вывод позволяет создать уравнение жидкого состояния вещества, что до сих пор не сделано в курсе общей физики.

 

 

Список литературы

 

1.                 Ландау Л. Д., Лившиц Е. М., Статистическая физика, ч. 1., М., Наука, 1976, 584 с.

2.                 Теплофизические свойства неона, аргона, криптона и ксенона, М., Издательство стандартов, 1976, 636 с.

3.                 Теплофизические свойства технически важных газов при высоких температурах и давлениях, М., Энергоиздат, 1989, 232 с.

4.                 Таблицы физических величин, М., Атомиздат, 1976, 1006 с.

5.                 Мейсон Э., Сперлинг Т., Вириальное уравнение состояния, М., Мир, 1972, 280с.

6.                 Белов В. Т., Термодинамика частных термодинамических систем, г. Саки, Райтипография, 1989 г., с. 44.