Строительство и архитектура

К.т.н. Корнюхин А.В., к.т.н., Снежкина О.В., к.т.н., Кочеткова М.В.

Пензенский государственный университет архитектуры и строительства

Моделирование работы ленточных ростверков свайных фундаментов с двухрядным расположением свай

В Пензенском государственном университете архитектуры и строительства уже несколько лет проводятся экспериментально-теоретические исследования железобетонных толстых плит, в частности исследования работы ленточных ростверков свайных фундаментов.

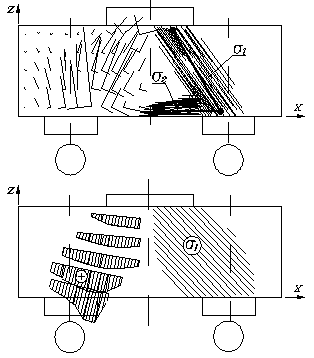
Были проведены многочисленные исследования на физических образцах - ростверков и теоретические исследования на основе численных методов. Как показал анализ результатов проведенных исследований, для таких конструкций, имеющих малый пролет среза, т.е. отношение ½ пролета в свету к высоте элемента, определяющую роль играют главные сжимающие и растягивающие напряжения s₁ и s₂, рис. 1.

Рис. 1 Распределение главных деформаций (напряжений)

Над опорным сечением в ростверках с двухрядным расположением свай

Главные напряжения имеют следующий характер распределения. Под грузовой площадкой сжимающие напряжения расосредотачиваются равномерно по длине ростверка. С удалением от верхней грани напряжения s₁ концентрируются в так называемые потоки, при этом наибольшая концентрация напряжений возникает у внутренних граней опорных площадок свай.

Следует отметить две характерные особенности распределения напряжений s₁ в сечении над опорами-сваями. Эти особенности связаны с пространственном характером работы ростверка и большими размерами поперечного сечения сваи.

Первая особенность заключается в том, что концентрированный поток главных сжимающих напряжений над сваями имеет два угла наклона, в продольном и поперечном направлении. Однако траектории распределения сжимающих напряжений s₁ в средней части потока имеют равномерный характер и один угол наклона в поперечном направлении. Таким образом, траектории главных сжимающих напряжений собирающиеся в пучок над опорой-сваей выделяют три характерные участка. Упомянутый выше средний участок с траекторией напряжений к горизонтальной поверхности только в поперечном направлении и два крайних участка с пространственным углом наклона складывающимся из двух углов, в продольном и поперечном направлении, рис.2.

Вторая особенность заключается в том, что эпюра распределения напряжений s₁ является симметричной относительно оси поперечного ряда сваи и состоит из трех характерных участков отличающихся величиной напряжений. Первый участок располагается в центре сваи, его длина составляет примерно 1/3 от продольного размера поперечного сечения сваи и характеризуется наименьшим значением сжимающих напряжений s₁. Второй и третий участки располагаются вдоль внутренней грани сваи в продольном направлении.

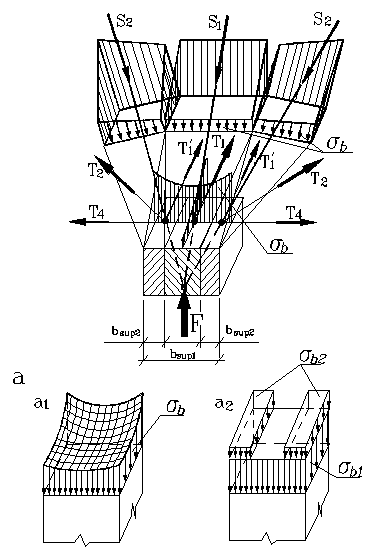
Рис.2 Особенности напряженно-деформированного

состояния ростверка над опорой -сваей:

а. Эпюра распределения сжимающих напряжений;

а₁. действительная; а₂. апраксимированная.

Длина их составляет также примерно 1/3 от размера сваи с максимальными напряжениями у грани. В целом эпюра распределения главных напряжений s₁ в опорном сечении имеет седлообразный характер, рис.2. При апраксимации действительной эпюры сжимающих напряжений в опорном сечении, предлагается следующие преобразование. От действия главных сжимающих напряжений, сосредоточенных в центре общего потока, принимается прямоугольная эпюра, охватывающая все сечение сваи. Данная эпюра соответствует среднему участку опоры. На крайних участках прямоугольная эпюра сжимающих напряжений дополняется трапециевидной эпюрой, которая получается от действия главных напряжений s₁ с пространственным углом наклона. В результате такого условного наложения эпюр, получается картина распределения напряжений над опорной площадкой с большой точностью приближающаяся к действительной, рис.2.

Траектории главных растягивающих напряжений s₂ имеют свои особенности обусловленные теми же причинами что и особенности s₁. Первая особенность заключается в том что концентрация напряжений s₂ отмечается в двух направлениях, в продольном и поперечном. Второй особенностью является то, что концентрация напряжений имеет седлообразный характер распределения зпюры вдоль опорной площадки также как и напряжения s₁ и примерно равномерный характер в пролете в продольном направлении. В поперечном направлении эпюра растягивающих напряжений также неравномерна.

В целом главные растягивающие s₂ и главные сжимающие s₁ напряжения, траектории которых равномерно распределяются под грузовой площадкой (стеновой конструкцией) и концентрируются в опорных сечениях над сваями образуют подобие силовой структуры внутри ростверка или условно говоря каркас. При этом главной отличительной особенностью ростверков будет являться их пространственный характер работы. В связи с тем, что для плоских коротких элементов уже разработана расчетная каркасно-стержневая модель описывающая прочность коротких элементов, целесообразно использовать принципы построения указанной модели и на ее основе построить пространственную каркасно-стержневую модель (ПКСМ) - модуль многократно повторяющийся по длине ростверка образуя расчетную модель системы.

Моделируя работу и напряженно-деформированное состояние ростверка выделено два элемента - расчетных модуля, рис.3. Первый модуль представляет собой пространственную стержневую модель, второй модуль представляет собой плоскую стержневую систему, аналогичную коротким балкам. По мере увеличения длины ростверка указанные модули объединяются над каждой сваей в единую систему состоящую, из двух крайних пространственных модулей и одного среднего плоского модуля, показанную на рис.3.

Рис.3 Пространственная и плоская каркасно-стержневая

модель ростверка с двухрядным расположением свай:

а. расчетная модель в плане. Схема расположения

грузовых площадок и ключевых точек модели.

Таким образом над каждой сваей располагается как бы три условных стержня расчетной модели имитирующие оси двух крайних потоков сжимающих напряжений и одного среднего потока, о которых говорилось выше. При этом указанные оси пересекаются с соответствующими осями трех потоков растягивающих напряжений. Средний поток располагается в поперечном, а два крайних потока расположенных в продольном направлении, рис.2.

Для построения пространственного и плоского стержневого модуля необходимо было решить две задачи. Во-первых, определить размеры условных грузовых и опорных площадок соответствующие каждому сжатому элементу ПКСМ, а во-вторых, определить положение ключевых точек, т.е. точек пересечения осей сжатых и растянутых условных элементов модели.

Для решения первой задачи было принято следующие условие. Верхняя ключевая точка пространственного модуля должна располагаться на вертикальной оси проходящей через середину поперечного и продольного пролета ростверка каждой пары свай. Верхняя ключевая тачка плоского модуля должна располагаться на оси проходящей через середину поперечного пролета каждой пары свай. Нижние ключевые точки трех модулей расчетной системы объединяющиеся над каждой промежуточной сваей должны лежать на продольной оси сваи в уровне центра тяжести арматурного пояса.

На основе геометрических построений и, с учетом оговоренных условий, разработана система расчетных зависимостей по которым определяются размеры условных опорных и грузовых площадок соответствующие трем расчетным модулям сходящимся над каждой промежуточной сваей, (рис.2, 3).

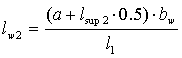, [1]

, [2]

где L - шаг свай в продольном направлении, м;

L₁ - шаг свай в поперечном направлении, м;

b_w - ширина грузовой полосы, м.

При этом длину среднего грузового участка l_w1 следует принимать не меньше длины сечения сваи, то есть l_w1 ³ l_sup

Величина l_w2 определяется из условия пропорциональности длин опорных и длин соответствующих грузовых участков.

, [3]

где а - расстояние от грани сваи до середины пролета, м;

l_sup2 - ширина бетона наклонной сжатой полосы на опоре, м;

l_w2 - длина грузового участка для крайнего потока сжимающих напряжений, м.

Определив и соединив центры тяжести грузовых и опорных площадок получим ключевые точки двух модулей. При этом оказывается, что верхние ключевые точки расчетных моделей, а также нижние ключевые точки, объединяющие три модуля располагающиеся выше верхней грани ростверка и ниже нижней грани ростверка, являются мнимыми и используются для обеспечения завершенности и определения усилий в расчетной модели. При этом, положение мнимых вершин (ключевых точек) расчетных модулей не влияет на величину усилий в элементах модели. Вершины нижних ключевых точек расчетных модулей объединяются по контуру ростверка, для пространственного КСМ и вдоль поперечного пролета для плоского КСМ. В результате образуются пространственный и плоский расчетные модули, рис.3. Автоматически определяются пространственные углы наклона сжатых наклонных элементов в ПКСМ и плоские углы наклона сжатых элементов в КСМ.

Произведя статический расчет пространственного и плоского модуля, определяются усилия в стержнях модели и формируются условия прочности по сжатой и растянутой зонам.