Д.т.н. Снежко В.Л.

Московский государственный университет природообустройства, Россия

Особенности планирования и статистической обработки данных экспериментального исследования напорных турбулентных потоков

Существует более двух тысяч работ, посвященных экспериментальному изучению напорных потоков, среди них мировую известность имеют исследования И.Е.Идельчика, А.Д.Альтшуля, В.П. Зубова, Г. Фогеля, Е. Кинне, Д.Тома [3]. Тем не менее, необходимость изучения взаимного влияния местных сопротивлений, условий протекания жидкости в элементах трубопроводов сложной формы поперечного сечения, определение эквивалентной шероховатости трубопроводов из новых полимерных материалов и ряд других задач, стоящих перед инженерно-технической практикой в настоящее время, по-прежнему требуют проведения гидравлического эксперимента.

При исследовании гидравлических сопротивлений следует иметь в виду, что в переходной области коэффициенты местных сопротивлений зависят не только от геометрических характеристик каждого сопротивления, но и от чисел Re. Переход от зоны ламинарного течения к турбулентной имеет сложный характер и обладает индивидуальными особенностями в местных сопротивлениях различного типа. Большинство коэффициентов местных сопротивлений при напорном движении в трубопроводах не зависит от числа Рейнольдса при . Началу автомодельной области для различных местных сопротивлений соответствуют числа Рейнольдса: отвод –, тройник –, задвижка – .

Особенности поведения коэффициентов гидравлических сопротивлений в переходной и квадратичной зонах турбулентного режима должны учитываться еще на этапе планирования эксперимента. Основное условие проведения эксперимента – выполнение исследований в некотором диапазоне чисел Рейнольдса, отвечающем условиям подобия, для отслеживания динамики коэффициента Дарси l=f(Re) и коэффициентов местных гидравлических сопротивлений z=f(Re). При неизменных геометрических параметрах трубопровода непосредственно задаваемым в эксперименте фактором F является расход модельной установки или напор во входном сечении, изменение которого происходит регулирующим органом, имеющим свои характеристики. Генеральной совокупностью будут значения непосредственно задаваемого фактора, обеспечивающие на модели заданный диапазон чисел Рейнольдса. Объем генеральной совокупности N находится достаточно просто:

, (1)

где DF – размах фактора, обеспечивающих требуемые границы диапазона чисел Рейнольдса; Df – изменение фактора при минимально возможном перемещении регулирующего органа.

Выборочная совокупность формируется в процессе проведения эксперимента простым случайным бесповторным либо систематическим отбором.

При определении значения коэффициента l вначале следует использовать планирование однофакторного регрессионного эксперимента, целью которого будет построение уравнения парной линейной регрессии вида:

l=а₀+а₁×Re (2),

где а₀ и а₁ – коэффициенты уравнения регрессии.

Если в результате проверки статистического качества уравнения коэффициент а₁ будет признан незначимым, то трубопровод работает в квадратичной области гидравлических сопротивлений и дальнейшей целью исследований будет только интервальное оценивание среднего значения l.

В переходной области турбулентного режима l является функцией вязкости и эквивалентной шероховатости D_э материала стенок трубопровода, что в общем случае соответствует двухфакторному регрессионному эксперименту. Универсальные зависимости Кольбрука-Уайта и А.Д.Альтшуля [1, 5]:

(3)

(4)

хорошо описывают динамику l в переходной области, что было еще раз подтверждено экспериментальными исследованиями автора на трубопроводах круглого и квадратного поперечного сечения, поэтому поиск нового вида регрессионного уравнения не столь актуален. Динамику гидравлического коэффициента трения следует определять по зависимости:

, (5)

где А – коэффициент, зависящий от относительной эквивалентной шероховатости трубопровода .

В этом случае планирование эксперимента будет соответствовать построению уравнения парной регрессии. Для определения D_э по результатам экспериментальных исследований трубопроводов в переходной области гидравлических сопротивлений автором разработана методика, основанная на интервальном оценивании среднего значения, не требующая построения уравнения регрессии и дающая более точные результаты.

Изучение местных гидравлических сопротивлений или их узлов следует начинать с планирования однофакторного регрессионного эксперимента, вид уравнения которого соответствует общепринятой зависимости:

, (6)

где – коэффициент местного сопротивления в квадратичной области сопротивления; – коэффициент.

Если в результате статистического анализа качества уравнения незначимым будет коэффициент А, то исследуемый диапазон чисел Рейнольдса принадлежит квадратичной области и целью дальнейших исследований будет интервальное оценивание среднего значения . В противном случае сопротивление работает в переходной области турбулентного режима.

Для изучения взаимного влияния местных сопротивлений, расположенных на участке, меньшем, чем длина стабилизации течения за первым из них, необходимо получить значения всех коэффициентов в одном и том же диапазоне чисел Рейнольдса. Коэффициент взаимного влияния определяется по зависимости:

, (7)

где , z₁, z₂ – коэффициенты местного сопротивления пары взаимодействующих элементов и каждого из них.

В ИСО 5725 для описания точности метода измерений используется правильность, характеризующая степень близости среднего арифметического значения большого числа результатов измерений к истинному, и прецизиозность – степень близости результатов измерений друг к другу. Автором была выполнена оценка условий прецизионности для серии гидравлического эксперимента, применена международная стандартизация для определения числа повторов на одном уровне фактора, способа осреднения измеряемой величины и отсеивания выбросов, методика оценки параметров распределения серии и сравнения результатов, полученных в разных сериях.

При проверке принадлежности исследуемого диапазона чисел Рейнольдса квадратичной области турбулентного режима или работе в переходной области объем выборочных исследований определяется качеством регрессионного уравнения, используемого для описания динамики гидравлического сопротивления. Опыт автора показал, что удовлетворительные статистические оценки уравнения регрессии будут получены при соблюдении условия:

n = (3..5)×k, (8)

где n – число наблюдений в серии на различных уровнях независимого фактора, распределенных между левой и правой границами диапазона; k – число коэффициентов в уравнении регрессии.

Точность метода измерений в ИСО 5725 представляет собой сумму

, (9)

где m – общее среднее значение; B – лабораторная составляющая систематической погрешности в условиях повторяемости; e – случайная составляющая погрешности результата измерений в условиях повторяемости [2].

Получены зависимости для определения случайных и систематических погрешностей косвенно измеряемых величин, полученные на основании применения основных положений теории ошибок к принятым в гидравлике методам определения коэффициента Дарси l и коэффициентов местных гидравлических сопротивлений z (метод эквивалентных сечений):

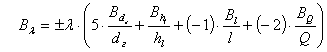(10)

(11)

(12)

, (13)

где Q – расход, h_l, h_loc – перепад давления между мерными створами, d_г – гидравлический диаметр.

Применение разработанной методики позволило определить значение эквивалентной шероховатости и оценить влияние использования ф.(3) и (4) на ее величину в трубопроводах с различной формой поперечного сечения. Среднее значение D_э при использовании формулы Кольбрука-Уайта ниже аналогичного значения, полученного при использовании формулы А.Д. Альтшуля, на 39% для трубопровода круглого сечения и на 13% для квадратных труб. Это обусловлено наличием вихрей и вторичных течений в углах трубопроводов квадратного сечения, вызывающих неравномерное распределение напряжений трения на границах потока, а также областью переходной зоны, в которой работали исследуемые трубопроводы.

Использование ф.(5) позволило получить выражения для определения l в переходной области в трубах квадратного и круглого поперечного сечения, вполне согласуются с обобщенной формулой А.В. Черникина [4].

На основании разработанной методики были выполнены многочисленные исследования тройников различной формы и узлов местных сопротивлений, включающих тройники, под руководством автора в лаборатории гидравлики МГУП получены значения коэффициентов взаимного влияния узлов «регулирующая задвижка - тройник».

Литература:

1. Альтшуль А.Д., Полякова Э.Н. К вопросу о потерях напора на трение в бетонных напорных водоводах // Вопросы гидравлики и водоснабжения / Тр. МИСИ. 1980. Сб. № 174. С. 25-30.

2. ГОСТ Р ИСО 5725-1 – 2002. Точность (правильность и прецизиозность) методов и результатов измерений. Ч.1 Основные положения и определения. Введ. 2002-04-23. М.: Изд-во стандартов, 2002. 24 с.

3. Идельчик, И.Е. Некоторые замечания по поводу гидравлических потерь, возникающих при движении реальной жидкости (газа) в напорных системах / И.Е. Идельчик // Известия вузов. Энергетика. – 1975. – № 9. – С. 99 – 104.

4. Черникин А.В., Талипов Р.Ф. Об использовании уравнения Кольбрука при гидравлическом расчете трубопроводов по обобщенной формуле // Трубопроводный транспорт. 2010. №4 (20). С.14 – 16.

5. Colebrock F. Turbulent flow in pipes with particular reference to the transition region between the smooth and rough pipe laws // Journal of the Inst. of Civil engineers. 1939. N 4.