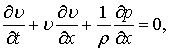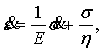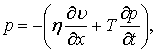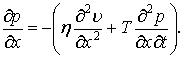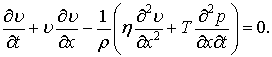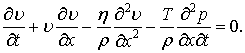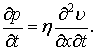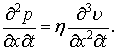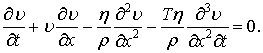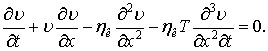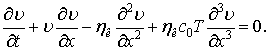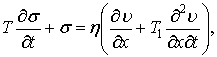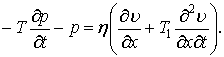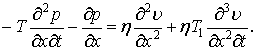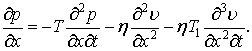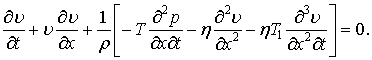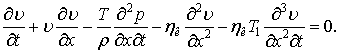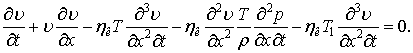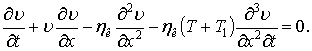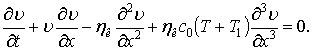Д. т. н., професор Нагорний В.П., к. т. н.
Денисюк І.І., Швейкіна Т.А.,
Юшицина Я.О.
Інститут геофізики ім. С.І. Суботіна НАН
України
НЕЛІНІЙНІ ХВИЛІ У В’ЯЗКОПРУЖНИХ СИСТЕМАХ
Останніми
роками теорія нелінійних хвильових процесів переживає новий підйом, що
пов’язано з розвитком двох основних напрямів. Це, по-перше, широке впровадження
нових математичних методів вивчення локалізованих збуджень в гідродинаміці і
теорії поля в формі відокремлених хвиль (солітонів), дисипативних структур,
самопідтримуючих коливань і т. п.; по-друге, в динаміці твердого
деформованого тіла відбувається процес становлення нових математичних моделей,
які враховують реальні явища внутрішнього руйнування і дисипації, що сильно
розширює діапазон хвильових задач і явищ, які розглядаються.
В
роботі [1] з використанням найпростіших моделей в'язкопружного середовища
розглянуті питання поширення хвиль тиску при імпульсній дії і частотні
характеристики цих збурень. Нижче із застосуванням складніших реологічних
моделей середовища буде показано
існування в ній нелінійних хвиль.
Дослідження
нелінійних хвильових процесів дозволяє виявити ряд якісно нових режимів рухів,
обумовлених взаємодією нелінійності, дисперсії і дисипації (в'язкості).
Аналітичною основою цих досліджень, як правило, є рівняння
Бюргерса-Кортевега-де Вріза (БКдВ). Покажемо, що рух в'язкопружних рідин (до
них відноситься і нафта) описується рівнянням БКдВ.
Одновимірний
рух ідеальної нестисливої рідини описується рівнянням [2]:
|
|
(1) |
де υ – швидкість руху; ![]() – тиск;
– тиск; ![]() – густина рідини.
– густина рідини.
У випадку нестисливої рідини (![]() ) рівняння нерозривності приймає вигляд:
) рівняння нерозривності приймає вигляд:
|
|
|
Припустимо,
що поведінка в’язкопружної рідини описується реологічним рівнянням стану
Максвелла [3]
|
|
(2) |
де ![]() – деформація;
– деформація; ![]() – швидкість
деформування;
– швидкість
деформування; ![]() – напруження;
– напруження; ![]() (швидкість
навантаження);
(швидкість
навантаження); ![]() – модуль пружності; η – коефіцієнт динамічної
в’язкості.
– модуль пружності; η – коефіцієнт динамічної
в’язкості.
Рівняння (2) представимо у вигляді:
|
|
(3) |
Враховуючи, що для рідини ![]() (
(![]() – тиск) і
– тиск) і ![]() із співвідношення (3)
маємо:
із співвідношення (3)
маємо:
|
|
(4) |
де ![]() – час релаксації в’язкопружної
рідини.
– час релаксації в’язкопружної
рідини.
Продиференціюємо вираз (4) за змінною ![]() :
:
|
|
(5) |
З урахуванням (5) вихідне
рівняння руху (1), має вигляд:
|
|
|
Після перетворення рівняння (1), отримаємо:
|
|
(6) |
Для ідеальної в’язкої рідини виконується
співвідношення [2]
|
|
|
або
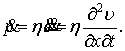
Отже,
|
|
(7) |
Диференціюючи співвідношення (7) за змінною ![]() , отримаємо:
, отримаємо:
|
|
(8) |
З урахуванням
(8) рівняння (6) має вигляд:
|
|
(9) |
Враховуючи, що 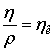 (
(![]() – коефіцієнт кінематичної в’язкості), з рівняння (9) маємо:
– коефіцієнт кінематичної в’язкості), з рівняння (9) маємо:
|
|
(10) |
Приймаючи ![]() [4] (
[4] (![]() – рівноважна швидкість руху), рівняння (10) представимо у
вигляді:
– рівноважна швидкість руху), рівняння (10) представимо у
вигляді:
|
|
(11) |
Рівняння (11) – це
нелінійне рівняння Бюргерса-Кортевега-де Вріза. В цьому рівнянні ![]() характеризує
кінематичну в’язкість рідини; параметр
характеризує
кінематичну в’язкість рідини; параметр ![]() характеризує
дисперсію.
характеризує
дисперсію.
Розглянемо другий
випадок, коли поведінка в’язкопружної рідини описується реологічним рівнянням
стану [5]
|
|
(12) |
де ![]() – напруження зсуву; η – коефіцієнт динамічної
в’язкості;
– напруження зсуву; η – коефіцієнт динамічної
в’язкості; ![]() – часи релаксації.
– часи релаксації.
Розглянемо одномірний рух в’язкопружної рідини, що описується рівняннями
(1) і (12). Систему цих рівнянь зведемо до одного диференціального рівняння.
При ![]() рівняння (12) має вигляд:
рівняння (12) має вигляд:
|
|
(13) |
Продиференціюємо (13) за змінною ![]() :
:
|
|
(14) |
Із (14) знаходимо ![]() :
:
|
|
(15) |
Підставивши співвідношення (15) в (1), отримаємо:
|
|
(16) |
В
рівнянні (16) перейдемо до параметра ![]() :
:
|
|
(17) |
Враховуючи раніше
отримане співвідношення (8), рівняння (17) представимо у вигляді:
|
|
|
Після алгебраїчних спрощень отримуємо:
|
|
(18) |
Враховуючи, що ![]() , із рівняння (18) маємо:
, із рівняння (18) маємо:
|
|
(19) |
Рівняння (19) – це
нелінійне рівняння БКдВ. В цьому рівнянні ![]() характеризує
кінематичну в’язкість; параметр
характеризує
кінематичну в’язкість; параметр ![]() – коефіцієнт
дисперсії.
– коефіцієнт
дисперсії.
Таким чином, дослідження хвильових рухів в обох випадках зводиться до
розв’язку нелінійного рівняння Бюргерса-Кортевега-де Вріза. Розв’язок цього
рівняння для деяких окремих випадків приведено в літературі [4, 6, 7].
Згідно [4, 7] вигляд стаціонарних розв’язків рівнянь (11) і (19) залежить
від співвідношень параметрів ![]() ,
, ![]() і
і ![]() ,
, ![]() . Для рівняння (11) критичне значення в’язкості
. Для рівняння (11) критичне значення в’язкості ![]() знаходимо із виразу [7]:
знаходимо із виразу [7]:
|
|
(19) |
У виразі (19) введені
позначення: ![]() ,
, ![]() (причому
(причому ![]() >
>![]() ). При
). При ![]() >
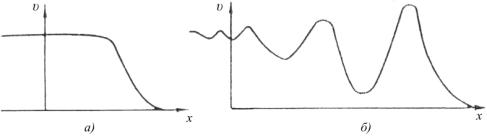
>![]() мають місце монотонні ударні хвилі (рис. 1, а), при
мають місце монотонні ударні хвилі (рис. 1, а), при ![]() <
<![]() ударна хвиля має осцилюючу структуру (рис. 1, б).
ударна хвиля має осцилюючу структуру (рис. 1, б).
|
|
|
Рис. 1. Монотонна (а) і осцилююча (б)
ударні хвилі [4] |
Аналогічно для рівняння (19)
знаходимо критичне значення в’язкості ![]() :
:
|
|
|
В цьому випадку нелінійне рівняння БКдВ не має аналітичних розв’язків і основним інструментом його
дослідження є чисельні методи. Результати деяких типових розв’язків рівнянь БКдВ приведені в монографії [4].
У якості таких розв’язків можуть бути і солітони, що є огинаючою
високочастотних коливань в середовищі [8]. Солітони, поширюючись на великі
відстані від свердловини, передають енергію імпульсного навантаження в
структурні елементи геофізичних середовищ з найменшою дисипацією.
Література:
1.
Нагорный В.П., Денисюк И.И.
Спектры и их приложения к задачам взрывного дела. – К.: «Ессе»,
2010. – 183 с.
2.
Лойцянский Л.Г. Механика жидкости и газа. –
М.: Наука, 1978. – 736 с.
3.
Ляхов Г.М. Основы динамики взрывных волн в грунтах и
горных породах. – М.: Недра, 1974. – 192 с.
4.
Накоряков В.Е., Покусаев Б.Г., Шрейбер И.Р.
Распространение волн в газо- и парожидкостных средах. – Новосибирск: Ин-т
теплофизики, 1983. – 238 с.
5.
Саттаров Р.М. Диагностирование релаксационных свойств
неньютоновских сред при их движении в трубах // Изв. Вузов «Нефть и газ». –
1981. – № 1. – С. 47–50.
6.
Кудряшов Н.А. Точные решения n-ного порядка с нелинейностью Бюргерса-Кортвега-де Вриза // Мат.
моделирование. – 1989. – Т. 1. – № 6. – С. 57–65.
7.
Березин Ю.А. Моделирование нелинейных волновых процессов.
– Новосибирск: Наука, 1982. – 160 с.
8.
Николаевский В.Н. Механизм
вибровоздействия на нефтеотдачу месторождений и доминантные частоты // Докл.
АН СССР. – 1989. – Т. 107. –
№ 3. – С. 570–575.