УДК 62-503.5

д.т.н., проф. С.Ф. Яцун, аспирант Л.Ю. Волкова

Юго-Западный государственный университет

Исследование влияния закона втягивания ноги в полете на высоту и длину прыжка многозвенного робота

Прыгающие роботы представляют собой развивающийся достаточно быстрыми темпами класс роботов, что объясняется их повышенной проходимостью при движении по неровной или пересеченной местности [1-4]. Многие прыгающие роботы в качестве разгонного модуля, посредством которого осуществляется отрыв от поверхности, используют ногу, которую затем втягивают во время полета, а приземляются на корпус. При таком конструктивном решении нога не испытывает ударных нагрузок и может быть достаточно легкой по сравнению с корпусом объекта. Целью данной работы является выявление влияния на высоту и длину прыжка устройства способа втягивания ноги во время полета.

Исследуемый прыгающий робот состоит из четырех звеньев i=1÷4, связанных между собой приводами вращательного 5, 6 и поступательного 7 движения (рис. 1). Звено 3 закреплено в центре симметрии звена 4 – точке С₄. Причем звено 1 соответствует стопе, звенья 2 и 3 – ноге, звено 4 – корпусу.

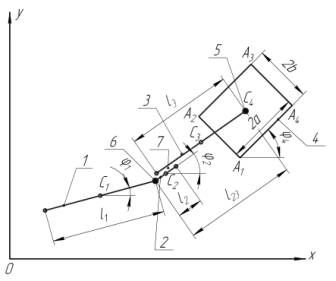
Рис. 1 Расчетная схема многозвенного прыгающего робота

Движение робота будем рассматривать в вертикальной плоскости Оху, в которой звенья i=1÷3 представляют собой стержни длинами l_i, а звено 4 имеет вид прямоугольника с размерами 2ax2b. Массы звеньев m_i сосредоточены в центрах их симметрии – точках С_i. Углы наклона звеньев к оси Ох равны φ₁, φ₂, φ₃₌φ_2, φ₄, относительное перемещение звеньев 2 и 3 – l₂₃.

Прыжок устройства начинается из положения, в котором звено 4 робота находится на поверхности, звенья 1, 2 и 3 полностью втянуты в корпус (звено 4) l₂₃=l₂₃^min и расположены под некоторыми произвольными углами к горизонту: φ₁, φ₂, φ₃=φ₂ и представляет собой последовательность этапов:

1 этап – звенья 1 – 3, жестко связанные между собой, поворачиваются за счет момента, создаваемого приводом 5, до выполнения условия φ₂=φ₂⁰;

2 этап – звено 1 поворачивается под действием момента, формируемого приводом 6, до тех пор, пока не выполнится условие φ₁=φ₁⁰=180⁰;

3 этап – перемещение звена 2 и жестко связанного с ним звена 1 относительно звена 3 при помощи силы, генерируемой приводом 7, до взаимодействия звена 1 с поверхностью;

4 этап - перемещение звеньев 3 и 4 относительно 2 за счет создаваемой приводом 7 силы до отрыва звена 1 от поверхности, при этом l₂₃=l₂₃⁰;

5 этап – полет робота, втягивание звеньев 1 и 2 в корпус робота при помощи привода 7 до выполнения условия l₂₃=l₂₃^min;

6 этап – приземление робота на одну из точек корпуса, в которой происходит абсолютно неупругий удар;

7 этап – поворот всех звеньев робота относительно точки опоры до тех пор, пока корпус не займет устойчивого положения.

Циклограмма напряжений, подаваемых на приводы во время одного прыжка робота, показана на рис. 2.

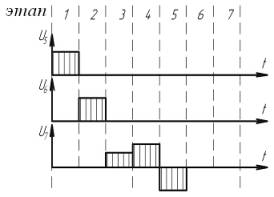
Рис. 2 Циклограмма напряжений за один прыжок робота

Движение системы в плоскости Оху описывается шестью обобщенными координатами: проекциями х₁, у₁ положения центра масс звена 1 на оси Ох и Оу на этапах 2 и 4 (проекциями х₄, у₄ положения центра масс звена 4 на соответствующие оси на остальных этапах), углами φ₁, φ₂, φ₄, относительным перемещением l₂₃ звеньев 2 и 3.

Система дифференциальных уравнений движения прыгающего робота представлена в матричной форме:

.

где , , - матрицы коэффициентов, - матрица обобщенных сил, определяемые на каждом этапе прыжка.

Моделирование одного прыжка устройства проводится в программном пакете MathCAD по специально разработанному алгоритму при следующих начальных условиях: t=0, x₄=а, , y₄=b, , j₄=0, , j₁=π, , j₂=π/2, . Параметры робота в безразмерном виде равны: m₁=1, m₂=1, m₃=1, m₄=7, а=1, b=1, l₁=0.5, l₂=0.9, l₃=0.9, l₂₃^min=0.4, l₂₃⁰=1.8. Масштабные коэффициенты для перехода к безразмерным величинам равны М=0,05 кг, Т=0.1 с, L=0.1 м.

Будем рассматривать три варианта втягивания звеньев 1 – 3 в корпус робота во время его полета:

1. нога не втягивается в корпус,

2. нога полностью втягивается в корпус со скоростью v,

3. нога полностью втягивается в корпус под действием силы F.

Высота и длина прыжка представляют собой расстояния, пройденные центром масс корпуса с момента отрыва звена 1 от поверхности до достижения наибольшей высоты и до завершения прыжка соответственно.

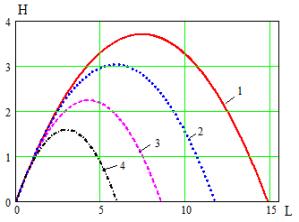
На рис. 3 приведены зависимости высоты прыжка робота от его длины при

φ₂⁰=π/3, F₂₃=160, l₂₃⁰=1,8, по которым видно, что в первом из описанных случаев робот будет совершать прыжок на наибольшие высоту и длину, причем значения данных параметров соответствуют значениям высоты и дальности полета тела, брошенного под углом к горизонту, определяемым аналитически, что свидетельствует о достаточной точности разработанных алгоритма и программы. Траектория прыжка робота при равномерном втягивании ноги в корпус имеет вид параболы, выпуклость которой направлена вверх, втягивание ноги под действием силы F сильно меняет характер траектории.

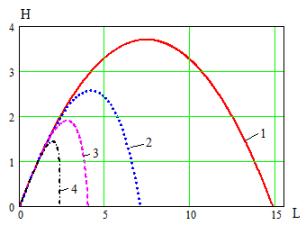
а б

Рис. 3 Высота и длина прыжка робота: а – 1 – v=0, 2 – v=2.5, 3 – v=5, 4 – v=7.5,

б – 1 – F=0, 2 – F=1, 3 – F=5, 4 – F=10

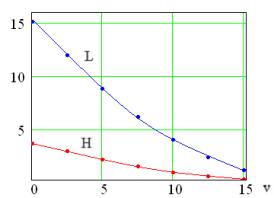
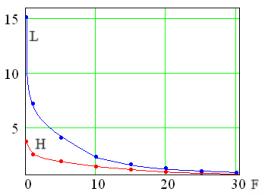
С увеличением скорости v и силы F высота и длина прыжка убывают по некоторым криволинейным зависимостям (рис. 4), причем при постоянной скорости v кривая убывает достаточно плавно, а при действии силы F вначале наблюдается резкое падение высоты и длины прыжка, а затем их плавное убывание.

а б

Рис. 4 Зависимости: а – Н(v), L(v), б – Н(F), L(F)

Результаты, полученные в ходе исследования, могут использоваться при проектировании многозвенных прыгающих роботов для выбора оптимального с точки зрения высоты и длины прыжка закона втягивания ноги в корпус устройства.

Работа выполнена в рамках гранта РФФИ № 10-08-00769-а, госконтракта № П699 тема № 1.109.10ф.

Список литературы

1. Cherouvim E. P. N. Energy saving passive-dynamic gait for a one-legged hopping robot // Robotica. 2006. Vol. 24. No. 4. P. 491–498.

2. Kovac M., Schlegel M., Zufferey ·J.-C., Floreano D. Steerable miniature jumping robot // Auton Robot. 2010. - No. 28. P. 295–306.

3. Stoeter S. A., Rybski P. E., Papanikolopoulos N. Autonomous stair-hopping with scout robots. In IEEE/RSJ international conference on intelligent robots and systems. 2002. Vol. 1. P. 721–726.

4. Волкова, Л.Ю. Исследование движения многозвенного робота, перемещающегося с отрывом от поверхности / Л.Ю. Волкова, В.В. Серебровский, С.Ф. Яцун // Известия Юго-Западного государственного университета. 2012. - № 1 (40). Ч. 2. С. 12-18.