12.Автоматизированные системы управления на производстве

Головицына М.В.

Профессор кафедры РЭУС Александровского филиала Московского Государственного открытого университета им. В.С.Черномырдина, к.т.н.

Формирование исходных данных при построении математических моделей технологических процессов.

Метод факторного анализа

В работах [1 – 6] автором изложена методика комплексного использования математических методов для построения «сквозных» математических моделей технологических процессов.

Составной частью этой методики является необходимость формирования исходной информации для построения таких моделей. Для исследования сложного технологического процесса и управления им требуются описание, учёт, измерение и регистрация максимального количества параметров на каждой операции. Однако проведение полного перечня замеров по всему процессу в условиях производства затруднено и не всегда экономически оправдано. Поэтому уже на первых стадиях проектирования технологического процесса очень важно решение такой задачи: найти минимальное количество параметров, несущих максимальное количество информации. Другими словами, определить информативность параметров и тот процент их вклада, по которому с заданной погрешностью можно судить, что выгоднее: замерять ли этот параметр или отнести его к общей «поправке».

Сначала надо проводить выделение групп сильно коррелирующих между собой параметров по признаку их наибольшей коррелированности [7, 8].

После этого целесообразно применение методов факторного анализа для поиска обобщённых факторов и закономерностей при минимальном количестве параметров, несущих достаточную информацию о протекании процесса. После группировки проводится поиск информативных параметров внутри групп. Для этого используются методы главных факторов и главных компонент.

Линейная модель факторного анализа

(1)

где Z_j - j^й признак (величина случайная);

F₁,...,F_p - общие факторы (величины случайные, имеющие нормальный закон распределения);

V_j - характерный фактор;

a_j1,...,a_jp - факторные нагрузки, характеризующие существенность влияния каждого фактора (параметры модели, подлежащие определению);

d - нагрузка характерного фактора.

При этом исходными данными является матрица m x n; строки матрицы соответствуют объектам наблюдений (i=1,2,...,n), столбцы - параметрам (j=1,2,...,m).

Таким образом, для j^го параметра и i^го объекта модель (1) можно записать в виде:

, (2)

где F_ki - значение k^го фактора для i^го объекта.

Дисперсию признака S²_j можно разложить на составляющие: часть, обусловленную действием общих факторов - общность h²_i, и часть, обусловленную действием j-го характерного фактора - характерность a²_j.

Если общие и характерные факторы не коррелируют между собой, то дисперсию признака можно представить в виде:

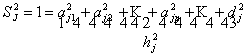(3)

Методы факторного анализа делятся на методы, требующие предварительной оценки общностей, и методы, требующие предварительной оценки числа факторов.

Одним из основных методов, требующих предварительной оценки общностей, является метод главных факторов. Этот метод состоит в решении упорядоченной цепочки связанных между собой экстремальных задач.

Надо найти максимум вклада V₁ фактора F₁

(4)

как функционала, зависящего от факторных нагрузок а_ij этого фактора на все параметры при условии, что матрица А факторных нагрузок удовлетворяет соотношению

, (5)

рассматриваемому в данном случае как ограничение на матрицу А.

В (5) принято:

А - матрица факторных нагрузок;

А’ - транспонированная к А матрица;

- редуцированная корреляционная матрица.

Далее решается задача нахождения максимума вклада V₂ фактора F₂:

(6)

как функционала, зависящего от факторных нагрузок а_j2 этого фактора при условии

, (7)

где А₁ - матрица факторных нагрузок 1-го фактора

и т.д. (8)

Фактически эта процедура сводится к нахождению собственных чисел и собственных векторов корреляционной матрицы . Этот метод даёт единственное решение.

Разновидностью метода главных факторов является метод главных компонент. Отличие состоит в том, что в методе главных компонент число факторов объявляется равным числу исходных параметров. Поэтому модель метода главных компонент можно рассматривать как преобразование одних координат в другие [9].

По методу главных факторов оцениваются общности (т.е. для каждого параметра оценивается суммарная дисперсия общих факторов) и число общих факторов. Расчёт осуществляется по формуле:

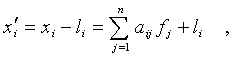(9)

где n - число общих факторов;

l_i - специфические факторы, некоррелированные между собой и с общими факторами.

Для нахождения нагрузок используется информация, заложенная в редуцированной корреляционной матрице (т.е. в корреляционной матрице R, у которой на главной диагонали вместо единиц стоят дисперсии величин x_i.). Расчёт проводится по формуле (8).

Адекватность факторной модели оценивается по матрице остатков (если величины ее коэффициентов малы, то модель считают адекватной). Для проверки полноты факторизации, т.е. числа общих факторов, целесообразно использование метода максимального правдоподобия [10]. Блок - схема факторного анализа приведена на рис.1.

Описание блоков.

Блок 1. Вычисление N и М; N- число наблюдений, М- число параметров.

Блок 2. Ввод EPS1, ITER, P1.

Блок 3. Ввод матрицы исходных данных X(i,j), i=1,…,M; j=1,…,N.

Блок 4. Вычисление и печать корреляционной матрицы Y(i, j), i=1,…, M; j=1,…,N, по формуле:

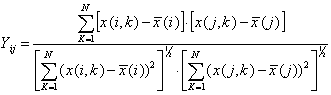, где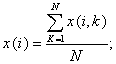

Блок 5. Нахождение общностей R(i), i=1,2,…, M.

Блок 6. Задается начальное значение матрицы A; A=Y

Блок 7. Проверка на условие KC>ITER.Если выполняется это условие, то переход на блок 15, если нет, то на блок 8.

Блок 8. Вызов подпрограммы нахождения собственных значений и собственных векторов матрицы А.

Блок 9. Упорядочивание собственных чисел матрицы , так, что (-новый порядок).

Блок 10. Нахождение факторных нагрузок.

Блок 11. Нахождение числа факторов.

Блок 12. Вычисление и печать новых общностей .

Блок 13. Проверка условия сходимости итерации ½R(i)Y(i,i)½<EPS1, i=1,2,…,M. В случае выполнения этого условия переход на блок 15, в противном случае переход на блок 14.

Блок 14. Замена старых общностей на новые, переход на блок 6.

Блок 15. Печать матрицы факторных нагрузок.

Полученные обобщённые факторы или отдельные параметры, которые вносят наибольший вклад, принимаются за наиболее информативные параметры и являются исходными данными при разработке математических моделей технологического процесса, объекта или отдельных технологических операций, т.е. при разработке математической модели системы.

Использование обобщённых факторов в качестве переменных в регрессионном анализе позволяет сократить число переменных, устранить коррелированность переменных, уменьшить влияние ошибок и - в случае ортогональности выделенных факторов - значительно упростить оценку значимости переменных.

РЕЗУЛЬТАТЫ ПРОВЕДЕНИЯ ФАКТОРНОГО АНАЛИЗА

Собственные значения:

1.3761 1.1345 1.1022 .9651 .7501 .6720

Собственные векторы:

.3470	.7920	.0008	-.2317	-.4426	-.0521
.5923	-.2533	.3329	-.5413	.3272	-.2723
.6880	.0043	-.2978	.5885	.2132	.2147
.0870	-.1026	.6522	.0516	-.2246	.7096
.1989	.4728	-.0321	-.1942	.7477	.3730
.0910	-.2730	-.6116	-.5163	-.2050	.4842

Вес Фактора в %:

Фактор 1	22.9358
Фактор 2	18.9081
Фактор 3	18.3704
Фактор 4	16.0843
Фактор 5	12.5018
Фактор 6	11.2002

К рассмотрению оставлено 4 фактора.

Факторные нагрузки:

	Фактор 1	Фактор 2	Фактор 3	Фактор 4
PaзB	.4071	.8436	.0009	-.2276
Ампл	.6948	-.2698	.3495	-.5313
УОтЦ	.8071	.0046	-.3126	.5781
УпрН	. 1020	-.1092	.6847	.0507
Рсиг	-.2333	.5036	-.0337	-.1908
РазС	.1068	-.2908	-.6421	-.5072

Вклад Фактора в переменную, в %

	Фактор 1	Фактор 2	Фактор 3	Фактор 4
РазВ	16.5725	71.1592	.0001	-5.1814
Ампл	48.2728	-7.2779	12.2175	-28.2775
УОтЦ	65.1456	.0021	-9.7746	33.4244
УпрН	1.0412	-1.1932	46.8824	.2568
Рсиг	-5.4419	25.3601	-.1132	-3.6386
РазС	1.1406	-8.4562	-41.2348	-25.7270

Здесь РазВ……. РазС – параметры технологического процесса изготовления видеоконтрольного устройства.

Литература

1. Головицына М.В. Методология проектирования РЭС. М.: МГОУ. 1993.

2. Головицына М.В. Проектирование автоматизированных технологических комплексов. М.: МГОУ. 2001.

3. Головицына М.В., Агаев И.А., Грозман П.Я. Применение математических методов для сжатия исходной информации при описании технологического процесса выращивания минералов. // Математические методы и АС в геологии. 1988. №12. М.: ЭИ ВИЭМС, 1988. Вып. 11 – 12.

4. Головицына М.В., Пупин А.А., Грозман П.Я. и др. Разработка основ моделирования и принципов построения АСУТП роста монокристаллов. Т.1 с приложениями. Научный отчёт. Гос. Регистрация №01830011460. Александров, 1984.

5. Головицына М.В. Статистический контроль качества. Методика выбора контрольных точек и контролируемых параметров. «Естественные и технические науки», 2008, №6.

6. Головицына М.В. Предварительная обработка производственной информации: сущность и необходимость. Журнал «Информационные технологии в образовании и науке», 2010. Вып.6. с.103-112.

7. Лоули, Максвелл. Факторный анализ как статистический метод. М.: Мир, 1967.

8. Трухаев Р.И., Горшков И.С. Факторный анализ в организационных системах. М.: Радио и связь, 1985.

9. Сажин Ю.В. Комплексное применение статистических методов в исследовании качества продукции. Саратов: Изд-во Саратов. ун-та, 1982.

10. Иберла К. Факторный анализ. М.: Мир, 1980.

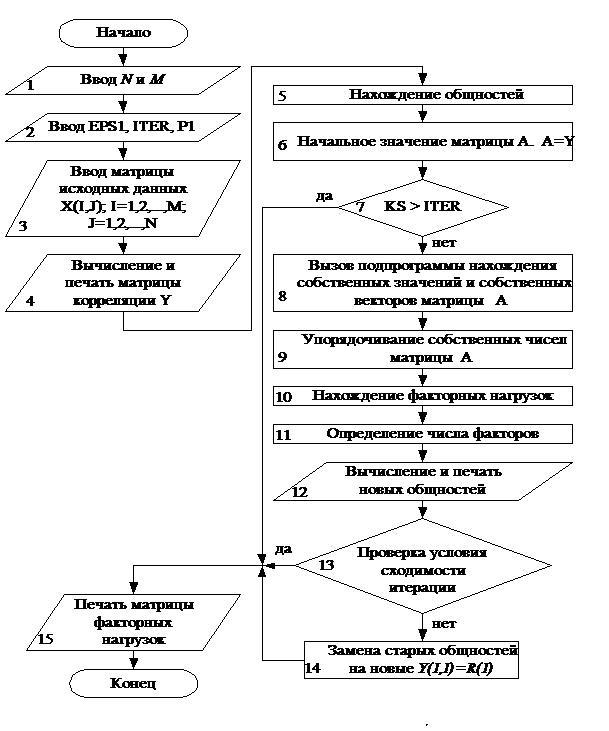
Рис. 1. Блок – схема факторного анализа