Технические науки/2. Механика.

к.ф.-м.н., доцент А.У. Нуримбетов А.У., Туреханова Г.С., Жанбосынов Р.С.

Таразский государственный университет им. М.Х. Дулати, Казахстан

Деформация естественно-закрученных многослойных анизотропных стержней при кручении и растяжении

В данной работе рассматривается деформация многослойных стержней при кручении и растяжении. При чем в последнем случае рассматривается напряженно-деформированное состояние (н.д.с.) естественно-закрученных стержней типа лопаток турбомашин. Принятая в настоящее время технология изготовления деталей, элементов конструкций из композиционных материалов (к.м.) имеет явно выраженную слоистую структуру [1]. Свойства отдельных слоев и их взаимное расположение в составе пакета таких слоев, в конечном счете определяют свойства всего материала. Поведение однонаправленного слоя полагается линейно-упругим, а связь между напряжениями и деформациями описывается обобщенным законом Гука. Соотношения между напряжениями и деформациями для слоя i определяются из формулы

. (1)

Параметры являются характеристиками упругости, , температура и тензор тепловых расширений i-го слоя к.м. [2].

С помощью геометрических представлений для слоистых анизотропных стержней с прямолинейной осью получены кинематические соотношения, которые в последующем использовались для установления основных уравнений.

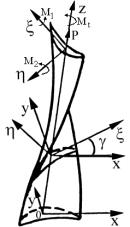
1. Геометрия закрученного слоистого стержня. При рассмотрении закрученных стержней используются две основные системы координат: неподвижная К_х и местная К_x (рис.1). В качестве неподвижной принимается прямоугольная правая система 0xyz. Начало координат 0 расположено в центре масс начального сечения. При этом ось z направляется вдоль хорды, ось х перпендикулярно волокнам, но в плоскости слоя и ось у, перпендикулярно слою. Оси x, h неподвижной системы координат xhV при движении вдоль оси поворачивается вместе с сечением, оставаясь главными центральными осями любого сечения. Ось V совпадает с осью z [3].

а б в

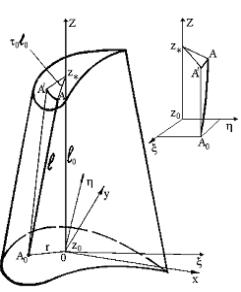
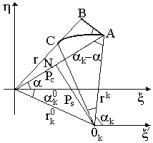
Рис.1. а) Основные системы координат для закрученных стержней; б) элемент закрученного стержня в) cхема определения деформаций элемента при повороте сечений.

Угол a(z) начальный угол закрученности стержня, отсчитываемый между осями х и x против движения часовой стрелки. Относительная закрученность t₀= стержня в текущем сечении z=V, при увеличении z образует винтовое волокно. Траектория перемещения точки А₀ в поперечном сечении z₀ при увеличении z образует винтовое волокно. Длина винтовой дуги АА₀ равна (рис.1б) (2), и она ортогональна плоскости поперечного сечения z₀+z =const.

2. Центр кручения закрученного стержня. Пусть под действием крутящих моментов М_t точка А поворачивается на угол t относительно центра кручения О_к [4]. Точка О_к удалена на расстояние под углом к оси x, а точка А в результате кручения занимает положение точки С (рис. 1в). Тогда ÈАВ=r_кt (r_к=|О_кА|= |О_кС|). В криволинейном треугольнике АВС

ÈАВ=ÈАС×cos(a_к-a)= r_кt cos(a_к-a), ÈВС=ÈАС×sin(a_к-a)= r_кt sin(a_к-a).

Здесь a_к , a - угол между радиусами векторов, исходящими из точек О_к и О. Опустив перпендикуляр из точек О_к на направление радиуса вектора ОА легко получить ÐОАО_к=a_к-a и поэтому r_кcos(a_к-a)=r-сos(a_к+a), r_кsin(a_к-a)= =sin(a_к+a). Следовательно, ÈАВ и ÈВС выражаются через текущие координаты относительно основной системы координат и величины, характеризующие положение центра кручения определяется из соотношений

ÈАВ= t(r-p_c); BC= p_st; r=|ОB|=|ОA|;

p_c=сos(a_к+a); p_s=sin(a_к+a); p_c +p_s=; |О_кN|=r-p_cx/r-p_st/r. (3)

3. Кинематика естественно закрученного стержня. 3а. Удлинение винтового волокна, обусловленное кручением t. В результате начальной закрутки t₀ и дополнительной закрутки деформации кручения t длина отрезка А₀А станет А₀В (рис. 2)

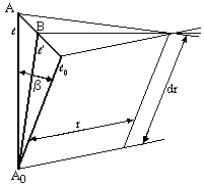
Рис. 2. Схема определения деформаций элемента при повороте сечений.

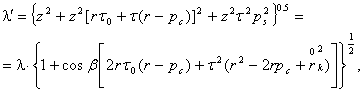(4)

где p_c, определяются из (3), а угол наклона волокна по отношению к оси стержня. Следовательно, удлинение винтового волокна, обусловленное кручением t, приближенно находится из выражения

, (5)

где р=r-p_c. При вычислении _t считались малыми члены, содержащие параметр t в третьей и более высоких степенях. Если центр кручения совпадает с осью стержня (=0, р=r) и при этом в выражении (5) сохранить первое слагаемое, то из него непосредственно следует соответствующее выражение работы [4].

3б. Удлинение винтового волокна, обусловленное растяжением и изгибом. Аналогично (4) вычисляется удлинение винтового волокна, обусловленное растяжениеми изгибом c₁, c₂. При этом, деформации находятся из выражения (6).

Здесь e относительное удлинение волокна за счёт растяжения, а c_j (j=1,2) - изменение его кривизны. При малых деформациях выражения (6) совпадают с соотношениями работ [5].

3в. Растяжение, изгиб и кручение винтового волокна. При сочетании растяжения, изгиба и кручения общая продольная деформация винтового волокна оценивается величиной (7), проекции которой на оси неподвижной системы координат К_х (8), определяют продольные и поперечные деформации стержня, обусловленные его начальной закрученностью.

В последующем исследовании кинематические соотношения для слоя i выбраны в форме (9), в которой - соответствуют значениям максимальной деформации поперечного сечения, обусловленной поперечными силами; величины позволяют оценить влияние перемещений в плоскости поперечного сечения на сдвиговые деформации и =0.5() деформации элементов поперечного сечения. Таким образом, в развитие работ [4], [5], [6] деформации определяются суперпозицией трех типов деформации и .

3. Равновесие закрученных стержней. При исследованиях равновесия стержней обычно применяют уравнения в интегральной форме, приводя напряжения в текущем сечении z₀ к статистически эквивалентной системе усилия Р и моментов М₁, М₂ , М_t , приложенных к оси стержня [4].

Величины Р, М₁, М₂ определяются как равнодействующие сила и моменты в поперечном сечении от нормальных напряжений s_zz

s_zz=, (10)

где и берутся из зависимости (9):

. (11)

При определении крутящего момента М_t необходимо учесть, что напряжения , действующие вдоль винтовых волокон под углом b=t₀r к поперечному сечению, имеют проекцию на поперечное сечение t₀r, которая вызывает дополнительный крутящий момент. Поэтому

(12)

Если в уравнение (11), (12) подставить выражения (10), то легко получить разрешающую систему уравнений (13), в котором вектор обобщенных сил определяется через вектор обобщенных деформаций и векторы , устанавливающие влияние поперечных сил, напряжений в плоскости сечения и температуры.

Система уравнений (13) является нелинейной относительно компонент вектора обобщенных деформаций . Максимальная деформация поперечного сечения (k=1,2) может быть выражена через заданные поперечные силы Q_j энергетическим методом [2], и определяется из равенства, аналогичных следующим

=-Q_kN_k, (к=1,2), 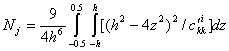, (j=1, k=4); (j=2, k=5). (14)

По найденным величинам вычисляется компоненты вектора в слое i.

Влияние напряжений и деформаций, действующих в плоскости поперечного сечения, может быть установлена итерационными методами, предложенными в [3], путем решения плоской задачи теории упругости. Координаты центра кручения могут быть найдены из условии к_j4=0 (j=2, 3). В работах [4], [5] уравнения (9) используется в линеаризованной форме (15), которая при необходимости может быть уточнена в соответствии с (8). В дальнейшем с помощью соотношения (2), (7) вычисляются напряжения в каждом слое i в рамках предположений, принятых при получении уравнений (15).

Характерной особенностью приведенных уравнений, связанных со слоистой структурой стержней, является то, что параметры к_mn (m,n=1,4) из матрицы К меняются от слоя к слою и для вычисления используются специально созданные программы. Кроме того, из-за изменения ориентации слоя относительно системы координат параметры упругости является переменными.

Следует отметить, что взаимосвязанность растяжения, изгиба и кручения являлось предметом многочисленных исследований. Однако в основном они касались стержней из изотропных материалов. В стержнях из слоистых материалов эта взаимосвязанность проявляется в большой мере из-за возможной структурной несимметричности. Так, например, в незакрученном стержне (t₀=0) параметры жесткости k_4j (j=1,2,3) могут отличаться от нуля и в связи с этим появляется эффект кручения при простом растяжении или изгибе.

Полученная приближенная теория закрученных слоистых стержней произвольного сечения основана на определенных гипотезах, позволяющих разделить компоненты напряжений и деформаций на главные и второстепенные, которым в ряде уравнений пренебрегается. Достоверность приближенной теории закрученных слоистых стержней проверяется сопоставлением с известными для некоторых частных случаев решениями и сравнением результатов расчетов с экспериментальными данными. Результаты расчета на ЭВМ по линейным соотношениям настоящей работы лучше согласуются с экспериментальными данными, чем существующие в литературе линеаризованные зависимости. Это подтверждает, что предлагаемое кинематическое соотношение (5) полнее отражает взаимовлияние деформации кручения и растяжения.

Литература:

1. Нуримбетов А.У. Автоматизированное проектирование раскроя деталей произвольного поперечного сечения из слоистых композиционных материалов // Вестник РУДН. Серия «Инженерные исследования». М.: - 2009 - №4.- С. 92-101.

2. Нуримбетов А.У. Решение задачи кручения слоистых композиционных стержней произвольного сечения методом конечных элементов //Строительная механика и расчет сооружений. М.: - 2009. -№4.- с.24-30.

3. Нуримбетов А.У. Полупространственная теория кручения композиционного слоистого стержня произвольного сечения. // Строительная механика инженерных конструкций и сооружений. М.: - 2010- № 1.

4. Биргер И.А. Пространственное напряженное состояние в лопатках с начальной закруткой. //Тр. ЦИАМ. - 1982. - № 996, с. 7-23.

5. Krenk S. The Torsion-Extstension Conpling in Pretwistet Elastic Beams. //Int. of. Solids Structures. - 1982.-V.19., №1, pp. 67-72.

5. Hodqes D.H. Torsion of Pretwistet Beams Due to Axial Loadinq. //J. Appl. Mech. - 1980. - V.42, №7, pp. 393-397.

6. Шорр Б.Ф. К экспериментальной проверке теории растяжения закрученных стержней // Изв. АН СССР. Механика твердого тела.- 1972. -№5. - С. 147-153.