С.В. Селезнева, В.В.Бурков
Пензенская
государственная
технологическая академия, г.
Пенза
ИССЛЕДОВАНИЕ
ЭЛЕКТРОДИНАМИЧЕСКОГО ВИБРОСТЕНДА С
ИСПОЛЬЗОВАНИЕМ МЕТОДОВ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ СИСТЕМ В
ПРОСТРАНСТВЕ СОСТОЯНИЙ
Задавая различные воздействия в
виде функций зависящих от времени можно моделировать состояние объекта и
отдельных его элементов также в виде функций зависящих от времени. Но в
некоторых случаях возникают задачи, связанные с исследованиями объектов в
частотной области. В таком случае применение подобных моделей оказывается
неудобным, так как приводит к увеличению количества моделирований. Гораздо
более эффективным решением подобной категории задач будет получение частотных
характеристик, по которым можно будет определить как резонансные частоты, так и
устойчивость системы в целом.
Рассмотрим схему
электродинамического вибростенда (ЭДВС) (рис. 1), который при использовании двух каналов управления с
непосредственными преобразователями электроэнергии (НПЭ) описывается системой,
включающей в себя дифференциальные уравнения Кирхгофа для обмоток возбуждения
длиной 
и подмагничивания с
активными сопротивлениями 
и индуктивностями
,
, на которые поданы управляемые от НПЭ с помощью
переключающих функций 
и 
напряжения
возбуждения 
и подмагничивания 
, изменяющиеся во времени 
, выражения для зависимостей силы 
от тока возбуждения 
и магнитной индукции 
от тока
подмагничивания.
Дифференциальные
уравнения механической части описывают трёхмассовую систему с коэффициентами
жёсткости 
и демпфирования 
, составленные на основе уравнений Лагранжа с перемещениями 
, скоростями 
для масс катушки 
, стола 
, испытываемого объекта 
[2].
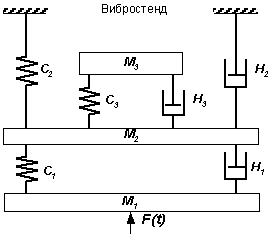
Рис. 1. Механическая часть электродинамического вибростенда
.
Примем 
соответственно 
, 
, 
, 
,
, 
и запишем
уравнение электродинамического стенда
в матричной форме [1]:
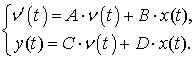
Передаточная функция
системы в пространстве состояний будет
определяться выражением
.
Проведем исследование ЭДВС
в частотной области [4].
Амплитудно-фазовая характеристика (АФХ) системы, также
называемая годографом Найквиста, определяется по выражению:
.
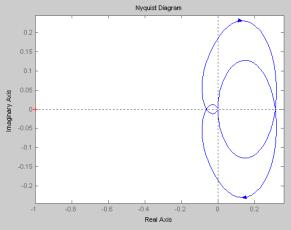
Рис.2. Амплитудно-фазовая характеристика (АФХ)
электродинамического вибростенда
График данной
характеристики представлен на рис. 2. В соответствии с критерием Найквиста система
является устойчивой, если АФХ разомкнутой системы не огибает точку -1, j0, что
мы и видим на данном графике.
Для определения
резонансных частот системы и фазовых сдвигов при различных частотах входного
сигнала удобно использовать амплитудно-частотную (АЧХ) и фазочастотную (ФЧХ) характеристики соответственно, определяемые следующими
выражениями:
,
.
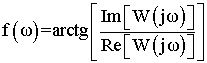Используя пакет Matlab,
построим данные характеристики (рис.3).
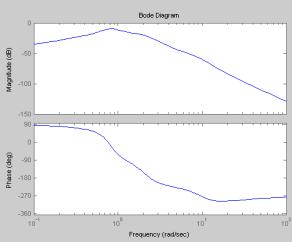
Рис. 3. Частотные
характеристики электродинамического вибростенда (амплитудно-частотная и фазочастотная характеристики)
Таким образом, исходная
модель, представленная в матричной форме физических уравнений, была
преобразована в две другие формы – форму пространства состояния и передаточную
функцию. Применение двух форм представления математических моделей механических
объектов позволяет облегчить процедуру исследования данных объектов за счет:
упрощения уравнений; взаимного преобразования форм представления моделей; более
полного использования функциональных возможностей
специализированных пакетов прикладных программ.
Литература:
1.
Прошина
Р.Д. Интегрированный комплекс компьютерно-имитационного моделирования
систем управления в виртуально-физической среде: автореф. дис. канд.
тех. наук. – Пенза, 2011. – 26с.
2.
Прошина
Р.Д. Математическое моделирование технических систем в нормальной форме
пространства состояний. // Известия Самарского научного центра Российской Академии
наук. – 2011. – №1. – С. 613–616.
3.
Сайт
компании mathworks – Режим
доступа – свободный. URL: http:// www.mathworks.com.