Технические науки/3. Отраслевое машиностроение

к.т.н. Павлов Е.И.

Южно-Российский государственный технический университет

(Новочерскасский политехнический институт), Россия

Анализ физических свойств грузов,

транспортируемых вертикальными винтовыми конвейерами

Основные грузы, перемещаемые вертикальными винтовыми конвейерами, - это сухие сыпучие материалы. К ним относятся как мелкокусковые (песок, щебень, комбикорм), порошкообразные (мука, цемент), пылевидные (штыб).

Стандартный подход к теоретическому описанию сыпучих материалов заключается в следующем. Берутся уравнения обычной гидродинамики и адаптируются с учетом специфики сыпучих материалов [1, 2, 3]. А именно, вначале выбирается такое уравнение состояния сыпучего материла, которое могло бы приводить к кластеризации. Далее, вводится дополнительный член, описывающий диссипацию энергии из-за неупругого столкновения частиц. Наконец, выбирается некая реологическая модель материала (модель, описывающая как материал деформируется и течет под действием напряжений) [4, 5, 6, 7].

Интересный подход к описанию макроскопических явлений к сыпучему материалу был использован в работе [8]. В ней исследовались нелинейные гидродинамические уравнения в достаточно общем виде, без выбора конкретной модели для той или иной характеристики жидкости. Авторы показывают, что можно ввести некий параметр порядка, который определяется через поле скоростей частиц. Возникающие же уравнения можно переписать в виде уравнений на этот параметр порядка. Эти уравнения будут содержать эффективный потенциал, минимум которого и даст нам решение для параметра порядка, а значит, и решение исходной задачи об эволюции системы.

В результате вся теоретическая конструкция приобретает совершенно новый смысл: теория становится разновидностью общей теории фазовых переходов второго рода (и критических явлений вообще) Гинзбурга-Ландау. 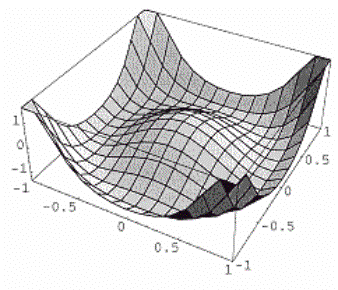Обычно в таких теориях естественным образом возникает некая критическая точка в эволюции системы, пройдя которую, система "перестраивается", претерпевает некий топологический переход, связанный с нарушением симметрии в системе. Параметр порядка при этом (рис.1) - это форма эффективного потенциала как функции параметра порядка, т.е. минимум достигается при целом множестве отличных от нуля параметров порядка и принимает ненулевое значение [9].

Рис. 1. Форма эффективного потенциала как функции параметра порядка.

Большинство сред являются дисперсными системами двух или трех фаз: это мелкие твердые частицы, распределенные в вязкой жидкости (суспензия или гель, если твердая фаза преобладает), или мелкие капельки одной жидкости в другой – эмульсия, или пузырьки воздуха в жидкости (пена), и т.д. Тем не менее, механика сыпучих сред рассматривает такую среду как однородную, но обнаруживающую такие же механические свойства, как и те, что установлены в опытах с реальным конкретным материалом. Этот подход, характерный для механики сплошных сред, позволяет избежать трудностей, связанных с изучением механизмов взаимодействия фаз, и сравнительно просто описать основные черты поведения реологических сред при воздействии на них заданных нагрузок.

Математическая модель механических свойств данной среды задается уравнением, связывающим напряжения, имеющиеся в окрестности некоторой точки среды, и деформации, возникающие вследствие этого, причем в это уравнение могут входить и скорости напряжений и деформаций, т.е. их производные по времени, и интегралы по времени от напряжений или деформаций .

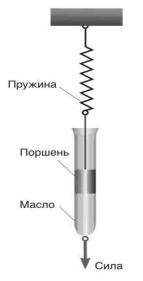
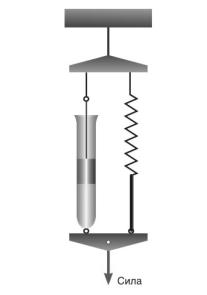
Среди уравнений, описывающих поведение среды в момент изменения внутреннего напряжения, выделяется схема, предложенная Кельвином, в которой упругий и вязкий элементы соединены параллельно, т.е. так, что их деформации одинаковы (рис. 2,а).

Соответствующее уравнение получается аналогично тому, как это сделано для среды Максвелла (рис. 2, б), но с учетом того, что в модели Кельвина одинаковы деформации элементов, а общее напряжение получается суммированием напряжений в вязком и упругом элементах .

В качестве описания потока сыпучего материала как вязко текучей жидкости со свойствами твердого тела используется аналитическая зависимость среды Бингама (рис. 3). Если напряжение в результате деформации совершенно пластичного тела (среда Сен-Венана) превышает некоторый предел, то тело дальше не оказывает сопротивления деформации. В области напряжений до предела текучести она представляет собой упругое тело, причем, в зависимости от увеличения напряжения, линейно возрастает и деформация [7, 8].

Для описания потока сыпучего материала в вертикальном винтовом конвейере принята среда Бингама, как наиболее адекватная модель, она наиболее верно отвечает заданным реологическим свойствам транспортируемых грузов [10].

а)	б)
Рис. 2. Реологическая модель описания среды Кельвина (а), Максвелла (б)

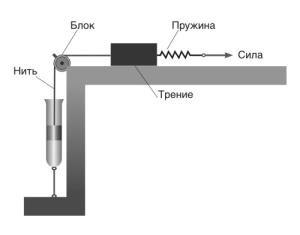
Рис.3. Механическая интерпретация среды Бингама.

Одним из направлений повышения производительности и снижения удельных энергозатрат вертикального винтового конвейера является рифление внутренней поверхности корпуса, позволяющее повысить поступательную составляющую силы, продвигающей поток материала вдоль оси конвейера, путем движения материала вдоль направляющих (рифлей).

Литература:

1. Евстратов В.А. Теория шнеконапорной подачи вязкопластичных материалов и шнековых модулей горных машин. Ростов-на-Дону. Издательство СКНЦ ВШ, 2000.- 160 с.

2. R. Olds, W. Olds, L. Bates, R. Mclntonsh – A radical approach to vertical convereyance jf bulk materials: the Olds Elevator/ Houston Maerial Handling Society, 2006

3. F.J.C. Rademacher – Some aspects of the characteristics of vertical screw conveyors for granular material/ Power Technology, 9 -1974, 71-89

4. Уръев H. Б. Физико-химическая динамика дисперсных систем // Успехи химии. — 2004. - Т. 73, № 1. - 39-62.

5. Matuttis H.-G., Luding S., Herrmann H. Discrete element simulations of dense packings and heaps made of spherical and non-spherical particles // Powder Technology. — 2000. — Vol. 109. - Pp. 278-292.

6. Gavrilova M., Rokne J. Collision detection optimization in a multi-particle system // Int. J. Comput. Geometry Appl. — 2003. — Vol. 13, no. 4.— Pp. 279-301.

7. Mustoe G. G. W., Miyata M. Material flow analyses of noncircular-shaped granular media using discrete element methods // J. Engrg. Mech. — 2001. — Vol. 127, no. 10. — Pp. 1017-1026.

8. Садовский В. М. Задачи динамики сыпучих сред // Мат. моделирование. — 2001. — Т. 13. — № 5. — С. 62-74.

9. Pournin L., LiebUng Т. M., Mocellin A. Molecular-dynamics force models for better control of energy dissipation in numerical simulations of dense granular media // Phys. Rev. E. — 2001.-Vol. 6 5 . - P . 011302.

10. Бабкин А.В., Селиванов В.В. Основы механики сплошных сред: Учебник для вузов – 2-е изд., испр. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. – 376 с.: ил. (Прикладная механика сплошных сред: В 3 т. / Науч. Ред. В.В. Селиванов; Т.1.)