УДК 539.3
Яхно Б.О.
к.т.н. доц.
НТУУ “Киевский политехнический институт”, г. Киев, Украина
МАЛОЦИКЛОВАЯ УСТАЛОСТЬ БОЛТОВОГО СОЕДИНЕНИЯ С ПРИМЕНЕНИЕМ УГЛЕПЛАСТИКОВ
Yakhno B.O. PhD,
The National Technical University of Ukraine “Kyiv
Polytechnic Institute”, Kyiv, Ukraine
LOW CYCLE
FATIGUE OF BOLTED JOINS WITH CARBON-FIBER-REINFORCED POLYMER.
___________________________________________________________________________________________
Анотация. Рассмотрено
напряженно-деформируемое состояние болтового соединения с центральной пластиной
из углепластика и боковыми пластинами выполненными из сплава ВТ-6. Проведено
численное моделирования работы данного соединения для случая растяжения.
Определены наиболее нагруженные элементы болтового соединения. Проведена оценка
ресурса (количества циклов до разрушения) болтового соединения. Задача решалась
в упругой постановке.
Ключевые слова: малоцикловая
усталость, углепластик, болтовое соединение.
Abstract.
We consider the stress-strain
state of bolted connection to the central
plate of carbon fiber and the side plates made of alloy VT-6. Numerical simulation
of the compound in the case
of extension. Identify the most loaded elements bolted connection. The estimation of the resource (the
number of cycles to failure) bolting.
The problem was solved in the elastic
formulation.
Keywords: low-cycle fatigue, carbon-fiber-reinforced
polymer, bolt joint.
ВВЕДЕНИЕ
Современные темпы развития техники
требуют от разработчиков все более рациональных технических решений. Применение
углепластиков вместо традиционных металлических материалов приводит к уменьшению собственного веса конструкции с
обеспечением параметров прочности и надежности работы конструкции на уровне
металлических материалов. Особенно это
актуально в аэро-космической отрасли, автомобилестроении. Уменьшение веса
конструкции позволяет уменьшить необходимую мощность двигателя, уменьшить
расход топлива, увеличить полезный вес и КПД машины.
Болтовое соединение входит в группу
наиболее распространенных соединений в машиностроении. Концентрация напряжений
вблизи такого соединения приводит к образованию усталостных трещин. Таким образом расчет на малоцикловую
усталость является необходимым элементом безопасной эксплуатации конструкции,
оценки остаточного ресурса и назначения времени необходимого технического
контроля.
1. ПОСТАНОВКА И РЕШЕНИЕ ЗАДАЧИ.
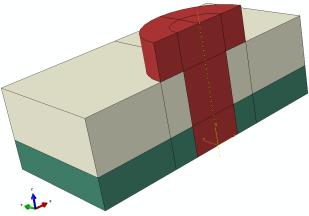
Объектом исследования является
образец болтового соединения, схема которого, представлена на рис.1.
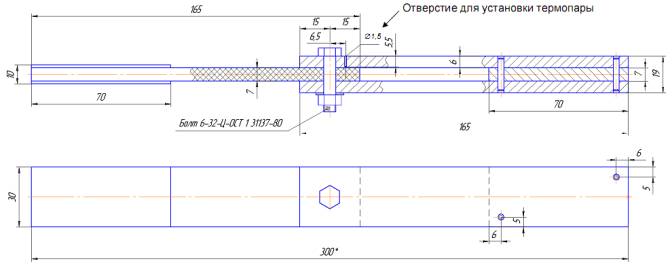
Рис.1.
Соединение представляет собой
сборку, в состав которой входит болт, выполненный из высокопрочной стали (Болт
6-32-Ц-ОСТ 1 31137-80), стягивающий две пластины из титанового сплава ВТ-6
толщиной 6 мм, между которыми находится
пластина из углепластика толщиной 7 мм и шириной 30 мм. Конструкция имеет две
плоскости симметрии.
В качестве материала бота была
выбрана высокопрочная сталь Н19К9М5Т со следующими механическими
характеристиками:
- Модуль Юнга ![]() МПа,
МПа,
- Предел текучести ![]() МПа,
МПа,
- Предел прочности ![]() МПа,
МПа,
- Относительное удлинение
пятикратного образца ![]() %,
%,
- Относительное сужение поперечного
сечения образца при статическом разрушении
![]() %,
%,
- Коэффициент Пуассона ![]() .
.
Для углеродного волокна принимались
следующие значения механических характеристик:
- Модуль Юнга ![]() МПа,
МПа,
- Предел прочности ![]() МПа,
МПа,
Для пластин из титанового сплава
ВТ-6 принимались следующие значения механических характеристик:
- Модуль Юнга ![]() МПа,
МПа,
- Предел прочности ![]() МПа,
МПа,
- Коэффициент Пуассона ![]() .
.
Согласно [1] допускаемая амплитуда условного упругого
напряжения ![]() при заданном
допускаемом числе циклов нагружения
при заданном
допускаемом числе циклов нагружения ![]() ≤ 1012
определяется как минимум из двух полученных значений согласно формул:
≤ 1012
определяется как минимум из двух полученных значений согласно формул:
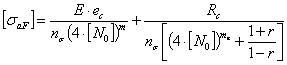 (1);
(1);
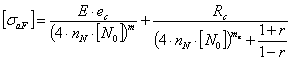 (2),
(2),
где ![]() - коэффициент запаса прочности
по напряжениям;
- коэффициент запаса прочности
по напряжениям;
![]() - коэффициент запаса
прочности по числу циклов;
- коэффициент запаса
прочности по числу циклов;
![]() и
и ![]() - характеристики
материала:
- характеристики
материала: ![]() ,
, 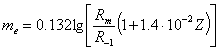 ;
;
![]() - коэффициент
асимметрии цикла напряжений;
- коэффициент
асимметрии цикла напряжений;
![]() - характеристика
прочности,
- характеристика
прочности, ![]() ;
;
с - характеристика пластичности, ![]() ;
;
![]() - предел
выносливости.
- предел
выносливости.
Для высокопрочной
стали Н19К9М5Т ![]() ,
, ![]() ,
, ![]() МПа,
МПа, ![]() МПа.
МПа.
Условия нагружения сборки следующие:
правые концы пластин из титанового сплава неподвижно защемлены, левый конец
углепластиковой пластины растягивается с усилиями ![]() кН и
кН и ![]() кН, что сответствует напряжению в "нетто" сечении
185 МПа. Коэффициент ассиметрии цикла нагружения
кН, что сответствует напряжению в "нетто" сечении
185 МПа. Коэффициент ассиметрии цикла нагружения ![]() .
.
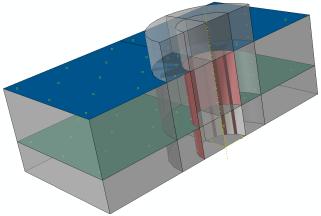
Так как конструкция симметрична, то
в расчетной модели была построена ее четверть. На рис.2 представлена
геометрическая модель сборки: коричневым цветом показан высокопрочный болт,
белым - пластины из титанового сплава ВТ-6, зеленым - углепластиковая пластина.
Между деталями введено контактное взаимодействие без учета сил трения,
контактирующие поверхности показаны синим, зеленым и коричневым цветом на
рис.3. Задача рассчитывалась в упругой постановке.
|
|
|
|
Рис.2. Геометрическая модель |
Рис.3 Контактное взаимодействие
между поверхностями. |
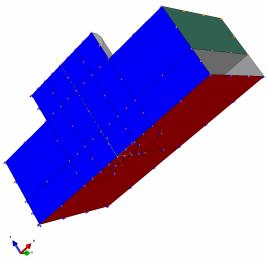
На рис. 4 показаны граничные условия,
приложенные к расчетной модели: плоскость, выделенная синим цветом имеет
граничные условия симметрии относительно оси Y (все перемещения вдоль оси Y равны нулю), плоскость, выделенная
красным цветом имеет граничные условия симметрии относительно оси Z (все перемещения вдоль оси Z равны нулю), плоскость, выделенная
зеленым цветом имеет жесткую заделку (перемещение вдоль каждой из осей X, Y, Z равны нулю). На рис. 5 показаны
приложенные нагрузки, так торцевая поверхность, выделенная зеленым цветом растягивается
давлением, интенсивностью 147 МПа, что соответствует напряжению в сечении
"нетто" 185 МПа.
|
|
|
|
Рис.4 Граничные условия |
Рис.5 Нагрузки |
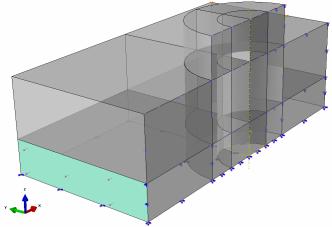
Геометрическая модель была разбита
на 24236 конечных элементов и 35341
узел (общее количество узловых неизвестных 83727). Дискретная модель представлена на рис.6. В модели использовались элементы типа С3D8R - твердотельные трехмерные линейные
восьмиузловые элементы призматической формы с сокращенным интегрированием
(напряжения определяются в точке интегрирования, находящейся по центру
элемента)
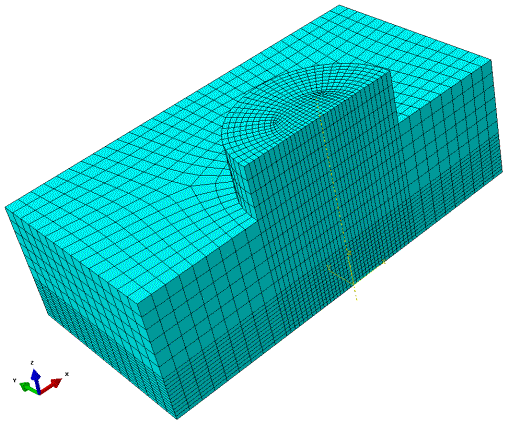
Рис.6 Конечно-элементная модель
2.РЕЗУЛЬТАТЫ РАСЧЕТА.
Результаты статического расчета
представлены на рис. 8-10.

Рис.8 Эквивалентные напряжения по
Мизесу для всей сборки

Рис.9 Эквивалентные напряжения по
Мизесу для Болта
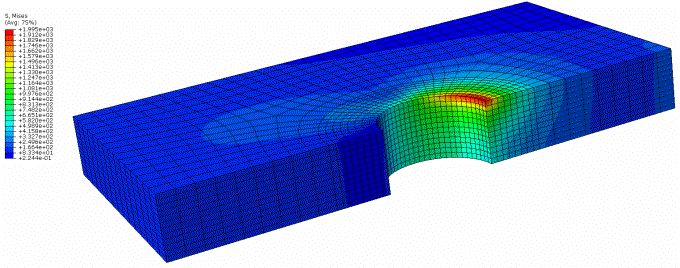
Рис.10 Эквивалентные напряжения по
Мизесу для углепластиковой пластины
Как видно из рис. 8 максимальные
напряжения в сборке наблюдаются в материале болта и углепластиковой пластины.
Таблица 1.
|
Элемент |
Уровень эквивалентных напряжений по
Мизесу, МПа |
Предел прочности
|
Предел текучести |
|
Болт |
1552 |
2180 |
1960 |
|
Углепластиковая
пластина |
1995 |
2500 |
- |
Как видно из таблицы 1 полученные
напряжения не превышают предел прочности и предел текучести, следовательно
статического разрушения не происходит (условие статической прочности по
предельному состоянию выполняется).
Экспериментально было показано, что
первым разрушается болт.
Задача решалась в контактной
постановке теории упругости, следовательно изменение внешней нагрузки приведет
к пропорциональному изменению внутренних напряжений в материале.
Максимальные эквивалентные
напряжения в материале болта составляют ![]() 1552 МПа, при
коэффициенте ассиметрии цикла
1552 МПа, при
коэффициенте ассиметрии цикла ![]() величина минимальных
напряжений в цикле
величина минимальных
напряжений в цикле ![]() 155,2 МПа, следовательно амплитуда напряжений за цикл
нагружения
155,2 МПа, следовательно амплитуда напряжений за цикл
нагружения
![]() =699 МПа.
=699 МПа.
Экспериментально было установлено,
что сборка при данном уровне нагружения простоит 132939 циклов.
Согласно зависимостей (1) и (2) для
материала болта была построена кривая усталости (рис.23), на этот же график
была нанесена точка с амплитудным значением напряжений ![]() =699МПа и числом циклов
=699МПа и числом циклов ![]() =132939.
=132939.
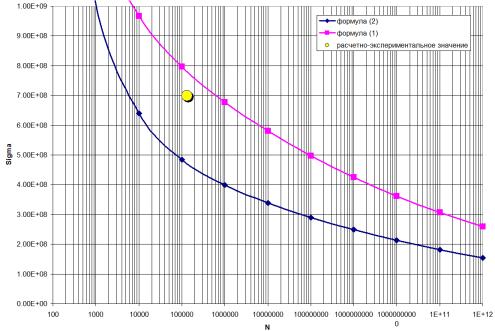
Рис. 11 Кривая усталости
Как видно из рис. 23 результаты
конечно-элементного расчета, эксперимента и расчета по стандарту совпадают.
Литература:
1.
Нормы
расчета на прочность оборудования и трубопроводов атомных энергетических
установок ПНАЭ Г 7-002-86. - М. Энергоатомиздат 1989. - 572с.
2.
Васильев
В.В. Механика конструкций из композитных материалов/
В.В.Васильев.-М. : Машиностроение, 1988.-288 с.
3. Getting
Started with ABAQUS. – USA, Abaqus inc., 2003 – 497c.
4. FKM
– Guideline, Analyt ical
Strength Assesment of Components in Mechanical Engineering, 5th,
revisied edition, English Version, Forshungskuratorium Maschinenbau (FKM),
Frankfurt/Main, 2003 – 268 c.