Азизов А.А.

Институт проблем геотермии ДНЦ РАН;

Махачкала, Россия; 367030, пр. И.Шамиля, 39а;

e-mail: azizov_amir@mail.ru

Зависимость полезной энергии геотермальной циркуляционной системы от температуры

закачиваемого теплоносителя.

 

Масштабное освоение геотермальной энергии связанно с использованием технологий геотермальных циркуляционных систем (ГЦС) Использование этой технологии позволяет интенсифицировать процесс добычи, повысить степень извлечения из недр тепловых ресурсов, а также решить проблему экологически безопасного сброса отработанных теплоносителей [1].

В процессе эксплуатации ГЦС значительны энергетические расходы системы на обратную, принудительную закачку отработанного теплоносителя в пласт. Принудительный характер закачки является основным недостатком ГЦС. Причиной этому служат большие капитальные вложения в строительство нагнетательной скважины и эксплуатационные затраты, связанные с принудительной закачкой термальной воды обратно в пласт.

Полезная мощность ГЦС определяется по следующей формуле [2]:

, (1)

где Wн - мощность, потребляемая насосом на нагнетание термальной воды обратно в пласт; Wп - полная мощность, вырабатываемая ГЦС.

Мощность полной энергии ГЦС определяется по формуле [2]:

, (2)

где G – массовый дебит одной добычной скважины, кг/с; с – удельная теплоемкость термальной воды, Дж/кг•0С; Т1 – температура добываемой ТВ, 0С; Т2 – температура нагнетаемой в пласт ТВ, 0С; η – коэффициент полезного действия получения электрической энергии из тепловой.

Мощность, потребляемая насосом для закачки ТВ, вычисляется по формуле [2]:

, (3)

где ∆Pн – давление нагнетания, который необходимо обеспечить, Па.

, (4)

где  – плотность воды при температурах нагнетания и добычи, кг/м3; H - глубина скважины, м; ∆Pг - гидравлические потери давления в скважинах и наземной теплотрассе, Па; ∆Pф - фильтрационные потери давления в пласте, Па; g – ускорение свободного падения, 9,8 м/с2.

, (5)

где Hд – глубина добычной скважины, м; Hн – глубина нагнетательной скважины, м; L – длина наземного трубопровода, м; λ, - коэффициент гидравлических потерь трубопровода; d – диаметр трубопровода, м;

, (6)

где k - проницаемость пласта, м2; h – мощность пласта; μн  – динамическая вязкость нагнетаемой обратно в пласт ТВ, Пуаз; R – радиус кругового контура питания, м.

Для проведения расчетов изменения энергетических затрат, для ГЦС с вертикальными скважинами, допустим следующие упрощения:

·                        плотности добываемой и закачиваемой воды равны;

·                        диаметры скважин и наземного трубопровода равны;

·                        дебиты нагнетательной и добывающей скважины равны;

При принудительном характере закачке ТВ обратно в пласт, используя нагнетательный насос, необходимо учитывать гидравлические  потери давления лишь в наземном трубопроводе и нагнетательной скважине. С учетом вышеописанного, и допущенных упрощений выражение (4) примет следующий вид:

, (7)

Подставляя выражение (7) в (3) получаем окончательную формулу для расчета мощности нагнетательного насоса для ГЦС с вертикальными скважинами.

С одной стороны, понижая температуру закачиваемой воды (T2), мы увеличиваем полную мощность (Wп), т.к. чем ниже , тем выше КПД такой системы: . С другой стороны, с уменьшением  растет вязкость (μн) закачиваемого обратно в пласт теплоносителя, а увеличение вязкости приводит к росту фильтрационного сопротивления, что в свою очередь увеличивает эксплуатационные расходы на обратную закачку (Wн). Температурную зависимость вязкости можно определить по следующей формуле [3]:

, (8)

где С – концентрация солей в воде, %, для расчета которой можно воспользоваться следующей формулой:

,

где M – минерализация пластовой воды, г/л.

Таким образом Wн является функцией вязкости μн (), в то время как μн является функцией Т2 (), следовательно, .

Из формулы (2) видно, что мощность полной энергии ГЦС зависит не только от температуры закачиваемой термальной воды (T2), а также от массового дебита (G). Дебит одиночной вертикальной скважины определяется по следующей формуле [4]:

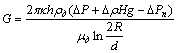, (9)

С учетом допущенных упрощений выражение (9) примет следующий вид:

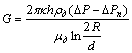, (10)

где ∆P – перепад давления между давлениями на границе кругового контура питания и на стенке скважины, Па; μд  – динамическая вязкость добываемой ТВ; ∆Pп – гидравлические потери давления в добычной скважине, Па; κ – горизонтальная проницаемость пласта, м2; h – мощность продуктивного пласта, м; ρ – плотность термальной воды, кг/м3;

Таким образом, возникает необходимость исследования изменения энергии полной мощности и энергии обратной закачки в зависимости от температуры закачиваемого теплоносителя Т2. Помимо этого важно знать зависимость времени функционирования ГЦС от дебита (G).

Время функционирования ГЦС, т.е. время в течении которого не будет происходить снижение температуры добываемой ТВ, можно определить пользуясь следующей формулой [5]:

, (11)

где l – расстояние между нагнетательной и добычной скважинами, м; m - пористость пород; h – мощность продуктивного пласта, м; cв – удельная теплоемкость ТВ, Дж/кг*°С; cпл – удельная теплоемкость водоносного пласта, Дж/кг*°С.

В табл. 1 приведены расчеты, проведенные для гипотетического месторождения со следующими параметрами: TПЛ=110 оС, H=2890 м, h=26 м, k=5,4·10-13 м2, cв=4,2 МДж/( м3 ·оС), cпл=2,5 МДж/( м3 ·оС), m=0,20, R=700 м, L=700 м, M=6,3 г/л.

 

Таблица 1. Изменения основных технологических параметров ГЦС при различных значениях температуры теплоносителя Т2.

∆Pн, МПа

Wн, МВт

Wп, МВт

Wпол, МВт

КПД, %

µн, Па*с

Т2,˚С

tтем, лет

G, кг/с

d=0,1 м

1,6948

0,0374

0,8278

0,7904

0,16

0,00054

50

8,55

20,97

1,9264

0,0425

1,1267

1,0842

0,18

0,00064

40

2,2595

0,0499

1,4716

1,4217

0,21

0,00078

30

2,7791

0,0613

1,8625

1,8011

0,23

0,00099

20

3,7031

0,0817

2,2994

2,2176

0,26

0,00138

10

d=0,2 м

1,8966

0,0653

1,2907

1,2254

0,16

0,00054

50

5,48

32,69

2,2316

0,0768

1,7568

1,6800

0,18

0,00064

40

2,7132

0,0934

2,2946

2,2012

0,21

0,00078

30

3,4646

0,1192

2,9041

2,7848

0,23

0,00099

20

4,8008

0,1652

3,5853

3,4201

0,26

0,00138

10

d=0,3 м

1,9107

0,0704

1,3818

1,3114

0,16

0,00054

50

5,12

35

2,2529

0,0830

1,8808

1,7977

0,18

0,00064

40

2,7449

0,1011

2,4565

2,3554

0,21

0,00078

30

3,5125

0,1294

3,1090

2,9796

0,23

0,00099

20

4,8774

0,1797

3,8383

3,6586

0,26

0,00138

10

 

Проведенные расчеты убедительно показали, что с понижением температуры Т2 мощность полной энергии растет, и значительно превосходит энергию, необходимую для обратной закачки. Так же увеличением дебита ТВ, который в свою очередь зависит от диаметра скважины, увеличивается Wпол однако время прорыва температурного фронта уменьшается. Однако т.к. в формуле (11) не учитывается приток тепла с кровли и подошвы водоносного пласта, вполне вероятно что снижение температуры будет происходит гораздо медленнее.

 

Литература:

 

1.                     Алхасов А.Б. Геотермальная энергетика: проблемы, ресурсы, технологии. – М.:Физматлит, 2008. – 376 с.

2.                     А.Б. Алхасов., Х.Г. Магомедбеков. Перспективы строительства ГеоТЭС на базе среднепотенциальных термальных вод.// Геотермия. Геотермальная энергетика: Сб. науч. тр., отв. редактор К. М. Магомедов. Махачкала, 1994, с. 17-34.

3.                     Гайдаров Г.М., Мавраева З.З., Рамазанов Ю.М. Влияние геофизических условий на плотность и вязкость глубокозалегающих флюидов. // ГЕОФИЗИЧЕСКИЕ МЕТОДЫ В ГЕОТЕРМИИ: Сб. науч. тр., 1986, вып. 6, с. 141-147.

4.                     Джаватов Д.К. Математическое моделирование геотермальных систем и проблемы повышения их эффективности. – Махачкала: Ин-т проблем геотермии ДНЦ РАН, 2007. – 248 с.

5.                     Лазурному берегу – геотермальное тепло // М.Г. Алишаев // АКТУАЛЬНЫЕ ПРОБЛЕМЫ ОСВОЕНИЯ ВОЗОБНОВЛЯЕМЫХ ЭНЕРГОРЕУРСОВ: Материалы IV Школы молодых ученных им. Э.Э.Шпильрайна./ Под ред. д.т.н. А.Б.Алхасов – Махачкала: ИП Овчинников (АЛЕФ), 2011, с. 44-49.