Д.т.н. Мещеряков В. Н., аспирант Цветков П. Е.

Липецкий государственный технический университет

Оптимальная по критерию минимума тока статора векторная система управления по главному потокосцеплению

Формирование момента асинхронного двигателя (АД) возможно воздействием на абсолютные значения векторов потокосцеплений ротора ψ_r, статора ψ_s и воздушного зазора ψ_m, токов статора i_s и ротора i_r. В данной статье рассмотрена векторная система, в которой моментообразующими векторами являются ток статора и потокосцепление воздушного зазора. Особенностью системы является то, что она обеспечивает поддержание оптимального угла между этими векторами.

Электромагнитный момент, развиваемый асинхронным электродвигателем, определяется следующим векторным произведением [1]:

(1)

Запишем уравнения электрического равновесия для обмоток статора и ротора АД [2]:

(2)

(3)

где – вектор напряжения, приложенного к статору;

R_s – активное сопротивление обмотки статора;

R_r - активное сопротивление обмотки ротора;

ω – мгновенная угловая скорость системы координат;

ω_r – мгновенная угловая скорость ротора двигателя.

Для решения этой системы уравнения ее необходимо дополнить уравнениями связи токов и потокосцеплений двигателя [2]:

(4)

(5)

где L_m – взаимная индуктивность обмоток статора и ротора;

L_s – индуктивность обмотки статора;

L_ls – индуктивность рассеяния обмотки статора;

L_r – индуктивность обмотки ротора.

Ток и потокосцепление ротора соответственно согласно [2]:

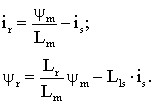(6)

Рассмотрим систему уравнений электромагнитного равновесия асинхронного электродвигателя в системе координат d-q, вращающуюся со скоростью поля ротора , которая неподвижна относительно поля статора [2]. Направим ось d вращающейся системы координат по главному потокосцеплению АД. При этом поперечная составляющая главного потокосцепления становится равной нулю (). Подставим полученные выражения (6) в (3) и выразим продольную составляющую главного потокосцепления:

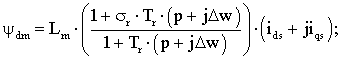(7)

где .

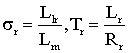При разделении данного выражения на мнимую и действительную части получим окончательное выражение для продольной составляющей главного потокосцепления. Таким образом, можно получить раздельное управление потоко-и моментообразующими векторами тока статора. Очевидно, что потокосцепление статора будет определяться только действительной часть выражения (8), а мнимую – запишем для дальнейшего определения Δω:

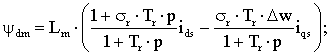(8)

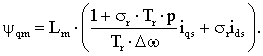(9)

Решая выражение (10) относительно Δω, получаем:

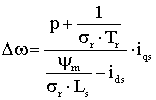. (10)

Моментообразующую составляющую тока статора выразим из выражения (1):

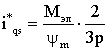. (11)

Данное математическое описание достаточно для построения системы векторного управления асинхронным электроприводом по главному потокосцеплению АД. Для наиболее эффективного использования системы необходимо найти оптимальные соотношения между моментообразующими векторами. Рассмотрим векторы тока статора и главного потокосцепления АД. При изменении угла между данными векторами можно привести параметры АД к условию минимума тока статора.

Электромагнитный момент АД в системе d-q при условии, что , принимает вид:

(12)

Выражение (4) в координатах d-q имеет вид [2]:

(13)

Подставим выражение для продольной составляющей главного потокосцепления из (13) в уравнение электромагнитного момента АД (12):

(14)

Рассмотрим векторную диаграмму АД в координатах главного потокосцепления, представленную на рис. 1.

Определим продольную составляющую тока ротора через поперечную составляющую тока статора:

(15)

где δ – угол между током ротора и осью d, который равен примерно 5,78⁰ согласно [1].

С учетом выражения (15) электромагнитный момент перепишется:

(16)

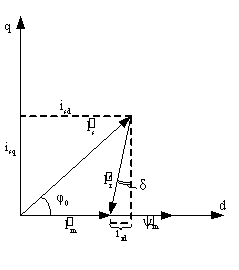
Рис.1. Векторная диаграмма АД

Представим составляющие тока статора в полярных координатах:

(17)

(18)

где φ₀ – угол между векторами тока и потокосцепления статора

I_sm – амплитудное значение тока статора.

Подставляя выражения (17), (18) в уравнение (16), формула электромагнитного момента приобретает вид:

(19)

Критерий минимума тока статора при фиксированном значении момента соответствует требованию максимума момента при фиксированном токе, который запишем в виде необходимого условия экстремума электромагнитного момента АД в установившемся режиме:

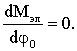(20)

Принимая во внимание необходимое условие экстремума (20) получаем следующее уравнение:

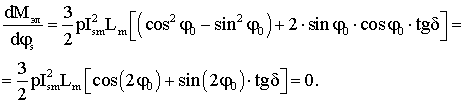
Решая данное уравнение находим оптимальный угол между током и потокосцеплением статора:

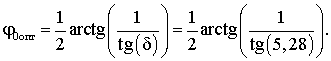(21)

В соответствии с формулой (21), приходим к выводу, что на нарастающем участке кривой намагничивания максимальное значение электромагнитного момента АД при фиксированном I_sm или, что то же самое, минимум I_sm при фиксированном M_эл имеет место для угла между током и потокосцеплением статора 42,36⁰.

Структурная схема оптимальной по критерию минимума тока статора векторной системы управления по главному потокосцеплению АД представлена на рис. 2.

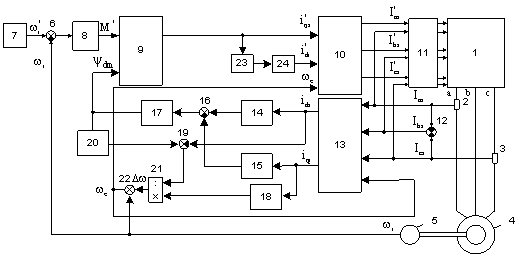
Рис. 2. Структурная схема оптимальной по критерию минимума тока статора векторная система управления по главному потокосцеплению

Представленная система содержит трехфазный инвертор 1, два силовых выхода которого соединены через датчики тока 2 и 3, подключенные к двум статорным обмоткам асинхронного двигателя 4, а третий силовой выход инвертора соединен с третьей обмоткой статора двигателя напрямую. На валу двигателя установлен датчик скорости 5, выход которого соединен с отрицательным входом блока сравнения 6, положительный вход которого подключен к блоку задания скорости 7, а выход блока сравнения подключен к входу пропорционально-интегрального регулятора скорости 8, выход которого соединен с одним входом блока задания поперечной составляющей тока статора 9, которая вычисляется по формуле (11). Выход блока 9 подключен к первому входу блока преобразования координат dq в ABC 10, имеющего три фазных выхода, каждый из которых соединен с первыми входами блока ШИМ - регуляторов тока 11, шесть выходов которого соединены с шестью управляющими входами трехфазного инвертора 1. Выходы датчиков тока 2 и 3 соединены с входами сумматора тока 12, также со вторыми фазными входами ШИМ регулятора тока 11 и входами блока преобразования координат ABC в dq 13. Выход сумматора тока 12 соединен с соответствующим входом блока 11 и фазным входом блока 13, выходы которых соединены с блоками определения продольной составляющей главного потокосцепления АД 14, 15, 16 по формуле (8). Также выходы блока 13 соединены с блоками определения угловой скорости токов ротора 18, 19, 20, 21 по формуле (10). На сумматоре 22 производится расчет текущей угловой скорости системы координат dq. Заданное значение продольной составляющей тока статора i_ds^* рассчитывается в зависимости от значения поперечной составляющей тока статора i_qs^* в блоке 23 согласно выражению:

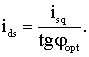
Блок 24 – задает максимальное и минимальное значение для i_ds^*.

Система построена таким образом, что достигается необходимое соотношение между продольной и поперечной составляющими тока статора, а соответственно и угол, между векторами тока и потокосцепления статора.

В настоящей статье разработана векторная система управления с опорным вектором главного потокосцепления АД с поддержанием оптимального угла между током и потокосцеплением воздушного зазора. Также определен оптимальный угол по критерию минимума тока статора между моментообразующими векторами для асинхронного электропривода.

Литература

1. Мещеряков В.Н. Системы асинхронного электропривода с управляемыми координатами моментообразующих векторов. Липецк: ЛГТУ, 2008. 120 с.

2. Соколовский Г.Г. Электроприводы переменного тока с частотным регулированием. М.: ACADEMA, 2006. 120 С.

Исследование выполнено при поддержке Министерства образования и науки Российской Федерации, соглашение 14.B37.21.0457.