Аскарова А.С., Болегенова С.А., Березовская И.Э., Оспанова Ш.С.

Казахский национальный университет имени аль-Фараби, Казахстан

Численное моделирование процессов горения двух видов жидкого топлива в зависимости от скорости впрыска

В наш век научно-технического прогресса и достижений в области компьютеризации и глобализации наука не стоит на месте. С развитием вычислительной техники, которая успела стать интеллектуальным помощником человека, исследователи добились немалых успехов в решении современных проблем теплофизики и физики горения и взрыва, связанных с эффективным использованием топливных ресурсов и учитывающих экономические и экологические аспекты процессов сжигания разных видов топлив.

В настоящее время одним из эффективных путей теоретического исследования является численный эксперимент, который в свою очередь развивается благодаря его использованию в многочисленных задачах теплофизики и усовершенствованию вычислительной техники. Численный эксперимент базируется на использовании математических моделей реальных процессов. Известно, что в топках электростанций сжигается твердое, жидкое и газообразное топливо. В этой связи использование численного эксперимента с привлечением средств вычислительной техники позволяет разработать новые технологии, требующие малых затрат и более совершенные методы численной реализации систем дифференциальных уравнений, описывающих процессы тепломассопереноса в камерах сгорания [1].

Моделирование процессов, протекающих при сжигании жидких топлив, является очень важным в связи с использованием распыленного топлива в различных технических устройствах. Горение жидкого топлива проходит через несколько стадий. Топливо впрыскивается в камеру сгорания, затем происходит испарение капель и смешение с окислителем, после чего наблюдается воспламенение и горение воздушно-топливной смеси. В данном процессе особую роль играет распыление топлива, так как эта стадия определяет эффективность горения самой смеси: чем меньше капля, тем быстрее происходит испарение, смешение с окислителем и воспламенение.

Численное исследование горения жидких топлив является сложной задачей теплофизики, так как требует учета большого количества взаимосвязанных процессов и явлений. Поэтому вычислительный эксперимент становится все более важным элементом исследования процессов горения и проектирования различных устройств, использующих процесс горения. Можно с уверенностью говорить, что его роль будет возрастать и в дальнейшем. Поэтому все большее распространение в теплофизике получают методы вычислительной гидродинамики, поскольку появляется возможность оптимизировать эксперимент на основе его виртуального прототипа [2, с. 859].

В настоящей работе описываются процессы распыла, воспламенения и горения жидких топлив в зависимости от скорости подачи топливной смеси в камеру сгорания. Изложены результаты по установлению зависимости теплофизических характеристик от скорости впрыска жидкого топлива в камере сгорания при заданных начальных и граничных условиях в разные моменты времени.

Математическая модель задачи осуществляется методами численного моделирования с использованием дифференциальных уравнений, описывающих турбулентное течение при наличии химических реакций. Она представляется основными уравнениями: неразрывности, движения, внутренней энергии, k-ε модель турбулентности, а так же начальными и граничными условиями.

Уравнение неразрывности для компоненты реакции m записывается следующим образом:

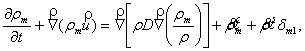(1)

где D – коэффициент диффузии, r_m – массовая плотность жидкой фазы, r – полная массовая плотность, – химический источниковый член; – источниковый член вследствие впрыска; u– скорость жидкости.

Уравнение переноса импульса для жидкости можно записать как:

(2)

где p – давление жидкости, a - безразмерная величина, A₀ равно 0 при ламинарном течении и 1 – при турбулентности.

Уравнение внутренней энергии имеет следующий вид:

(3)

и - источниковые члены, обусловленные тепловыделением в результате химической реакции и тепла, которое приносит впрыскиваемое топливо.

Математическая модель включает два дополнительных уравнения движения для турбулентной кинетической энергии k и скорости ее диссипации ε:

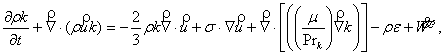(4)

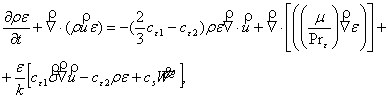(5)

Величина возникает вследствие взаимодействия с распылителем. Константы определяются из эксперимента [3].

Процесс горения жидких топлив рассматривается в модельной камере сгорания с форсункой, расположенной по центру нижней части камеры, через которую в поток окислителя (подогретый воздух) подается основная часть расхода жидкого топлива. Камера имеет конструкцию цилиндра высотой 15 см и радиусом 2 см. Начальная температура в камере сгорания равна 800 К. Количество контрольных ячеек - 600. Температура стенок камеры сгорания составляет 353 К. Площадь сопла инжектора составляет 2·10^-4 см².

В настоящей работе использовались два вида жидкого топлива: октан (C₈H₁₈) и додекан (C₁₂H₂₆). Химические реакции окисления для этих двух видов топлив представлены ниже:

2С₈Н₁₈ + 50О₂ = 16СО₂ + 18Н₂О

2С₁₂Н₂₆ + 37О₂ = 24СО₂ + 26Н₂О

Вычислительный эксперимент проводился при оптимальных значениях давления 100 бар для октана и 80 бар для додекана, и масс 6 мг для октана и 7 мг для додекана [2, с. 861]. Скорость впрыска жидкого топлива менялась от 150 м/с до 350 м/с. Нами было установлено, что при низких скоростях впрыска жидкого топлива, меньше 150 м/с, горение не происходит, так как скорость впрыска не является достаточной, для того, чтобы началось самовоспламенение и реакция горения стабилизировалась. Наиболее эффективно процесс горения октана и додекана протекает при скорости впрыскивания топлива 350 м/с, когда температуры в камере сгорания принимают максимальные значения (рисунок 1).

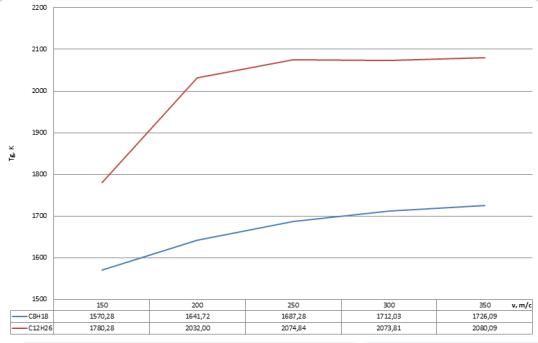
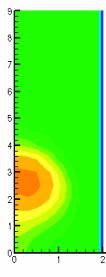
Рисунок 1 – Распределение температуры в камере сгорания (Т, К) в зависимости от скорости впрыска (v, м/с)

(синяя линия - октан (С₈Н₁₈), красная линия - додекан (С₁₂Н₂₆))

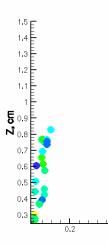
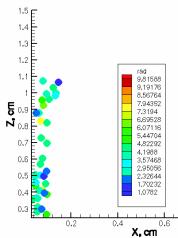
Результаты численного моделирования, приведенные на рисунках 2 и 3, показывают распределение капель жидких топлив по размерам и изменение температуры сжигания в камере сгорания при оптимальной скорости 350 м/с. В момент распыления все капли одного радиуса, но затем они испаряются, сталкиваются и сливаются, соответственно, меняя свои размеры. Значения радиусов капель показаны в микронах, при впрыскивании октана (рисунок 2 а, б). 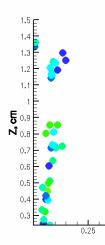Мы видим, что радиусы жидких частиц достигают 9,8 микрон, для додекана максимальный размер частиц составляет 8,8 микрона (рисунок 2 в, г). Согласно рисунку 1 основная масса капель имеет радиус порядка от 2 до 6 микрон, капли большего размера наблюдается редко. В случае додекана капли распространяются на больший объем в пространстве камеры, что соответствует 1,4 см по высоте и 0,25 см по ширине (рисунок 2 в, г), чем капли октана 1,1 см по высоте и 0,2 см по ширине (рисунок 2 б) камеры сгорания.

а) t=1,1∙10^-3с	б) t=1,8∙10^-3с	в) t=1,1∙10^-3с	г) t=1,8∙10^-3с

Рисунок 2 – Распределение капель октана а, б и додекана в, г по радиусам (rad, мкм) в различные моменты времени

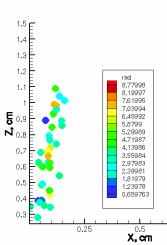
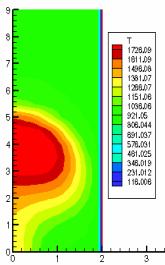
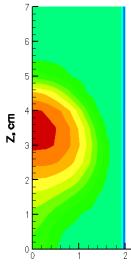
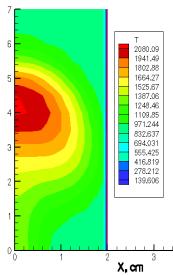
На рисунке 3 приведены графики изменения температуры при сжигании октана и додекана в камере сгорания со временем (3 мс, 4 мс). Когда смесь паров топлива с окислителем воспламеняется, то топливо быстро сгорает и почти вся область камеры по ширине охвачена факелом. Остальная часть камеры разогревается до 921 К (рисунок 3 а) и до 971 К (рисунок 3 в). Для октана область высоких температур является большей по размеру, чем при горении додекана. Ядро факела при сжигании октана занимает 2 см по высоте, 1 см по ширине камеры, при этом температура достигает 1726 К (рисунок 3 б), для додекана оно намного меньше 0,6 см на 0,25 см, соответственно, но максимальная температура составляет 2080 К (рисунок 3 г).

а) t=3,3∙10^-3с	б) t=4∙10^-3с	в) t=3,3∙10^-3с	г) t=4∙10^-3с
Рисунок 3 – Распределение максимальной температуры (Т, К) в пространстве камеры сгорания при сжигании октана а), б) и додекана в), г) в различные моменты времени

Анализ результатов вычислительных экспериментов показал, что, для оптимальной организации процесса горения октана и додекана необходимы особые условия для скорости впрыска жидкого топлива. Установлено, что при оптимальной скорости впрыска, равной 350 м/с, топливо сгорает без остатка, концентрация образующегося углекислого газа незначительна, а камера прогревается до высоких температур.

Полученные результаты могут быть использованы при проектировании различных технических устройств, использующих горение, которые решали бы одновременно проблему оптимизации процесса, увеличения эффективности сгорания топлива и минимизации выбросов вредных веществ.

Литература:

1. Аскарова А.С., Гороховски М.А., Рыспаева М.Ж., Волошина И.Э. Численное моделирование горения и самовоспламенения двухфазных химически реагирующих течений с впрысками// Известия Томского политехнического университета. ‑ 2009.- Т.315.-№4. - С. 5-9.

2. Askarova A., Ryspayeva M., Voloshina I. Numerical study of the influence of the spray velocity on the tetradecane’s combustion // Abstracts of The Conference on Thermal and Environmental Issues in Energy Systems ASME-ATI-UIT 2010, on Thermal and Environmental Issues in Energy Systems, Sorrento (Italy), 2010. – P. 859-862.

3.Amsden A.A., O'Rourke P.J., Butler T.D. KIVA-II: A computer program for chemically reactive flows with sprays. - Los Alamos, 1989. - 160 р.