Технические науки/6. Электротехника и радиоэлектроника

Ст. преп. Мирзакулова Ш.А., ст. преп. Балгабекова Л.О., студентка четвертого курса Мухамедсафа Л.

Алматинский университет энергетики и связи, Казахстан

О ФРАКТАЛЬНОЙ РАЗМЕРНОСТИ ИЗМЕРЕННОГО ТРАФИКА

На сегодняшний день существуют экспериментальные подтверждения о том, что поведение Internet трафика имеет самоподобную (фрактальную) структуру. Осуществим исследование измеренного магистрального трафика протокола TCP на самоподобие. При этом вычислены вероятностно-временные характеристики: математическое ожидание - 3,753; дисперсия - 140,04; среднеквадратическое отклонение - 11,8; коэффициент вариации 3,153) и составлен временной ряд интенсивности интервалов между пакетами TCP, представленный на рисунке 1.

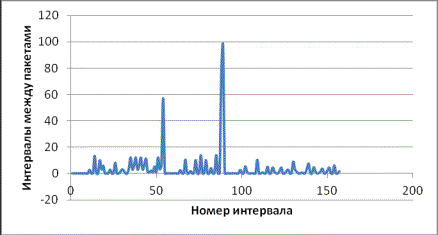
Рисунок 1 - Интенсивность интервалов между пакетами TCP

Этот трафик не обладает свойствами простейшего потока. Он имеет пульсирующий характер с существенной дисперсией.

Свойство самоподобия характеризуется тем, что при изменении шкалы измерений корреляционная структура рассматриваемого самоподобного процесса не изменяется [1]. На рисунках 2 и 3 представлены графики агрегированных процессов промежутков между поступлениями пакетов TCP для выявления свойств самоподобия, при этом выполнены уменьшение размера шкалы наблюдений сначала в 2 а потом в 3 раза.

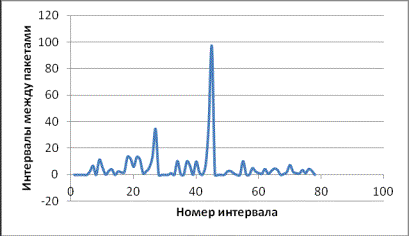
Рисунок 2 – График агрегированного процесса m=2

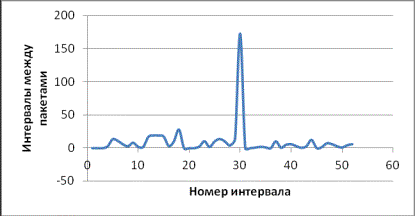
Рисунок 3 – График агрегированного процесса m=3

На основании выше приведенных графиков видно, что при изменении шкалы построения трафика, структура полученных рядов подобна структуре исходного ряда, то есть трафик самоподобен. Продолжим вычисления по процессу агрегирования для m=4 и определим дисперсию каждого агрегированного временного ряда (таблица 1). Согласно определению самоподобного процесса, имеет место соотношение дисперсий временных рядов: логарифмируя его получим .

Таблица 1 – Дисперсия агрегированных рядов

m	Dm
1	140,035	0	4,941
2	173,216	0,6931	5,154
3	621,398	1,0986	6,431
4	435,321	1,3862	6,076

Так как является константой, не зависящий от m, то график зависимости от представляет собой прямую с наклоном, равным . Построив график зависимости от и линию тренда (рисунок 4), определим аппроксимированное значение , =0,67. Учитывая, что параметр связан с показателем Херста Н как

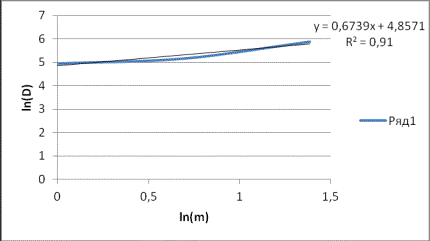
Рисунок 4 – Линия тренда для определения

Так как показатель H>0,5, то степень устойчивости долгосрочной зависимости исследуемого временного ряда выше среднего и ряд является самоподобным (фрактальным). Фрактальная размерность D временного ряда связана с показателем степени его фрактальности (показателем Херста) H формулой H = 2 - D. Фрактальная размерность равна D=2-H=2-0,66=1,34. Параметры самоподобия H и D представляют собой меры устойчивости статистического явления или меры длительности долгосрочной зависимости стохастического процесса.

Литература:

1. Шелухин О.И., Тенякшев А.М., Осин А.В. Фрактальные процессы в телекоммуникациях. - М.: Радиотехника, 2003.- 480 с.