Технические науки / 6. Электротехника и радиоэлектроника

 

К.т.н. Сухарьков О.В.

Одесская национальная академия связи им. А.С. Попова, Украина

Вынужденные колебания плоской осесимметричной струи

 

Разработка антенн передающих трактов дальней цифровой связи является важной проблемой информационной гидроакустики [1, 2]. Основными элементами излучающих антенн могут служить низкочастотные (0,2…5) кГц жидкоструйные преобразователи с круговым щелевым соплом в виде соосных дисков [3].  Доклад посвящен решению задачи вынужденных колебаний кольцевой струйной пластинки, являющейся моделью гидродинамического излучателя.

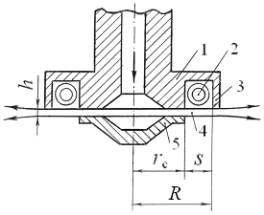
Рассмотрим механизм звукообразования преобразователя (рис. 1, а).

        

     

                     а)                                                                  б)

 

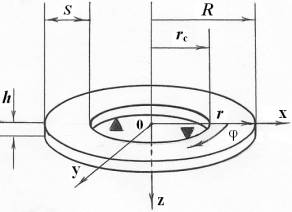
Рисунок 1 – Жидкоструйный преобразователь: а – схема, б – модель кольцевой струйной пластинки   

Затопленная струя, вытекающая из кругового щелевого сопла, образованного соосными дисками корпуса 1 и обтекателя 5, формируется в  плоскую осесимметричную струю 4. Ступенчатое препятствие 3 способствует тому, что часть кинетической энергии струи расходуется на формирование в проточке корпуса 1 тороидального вихря 2, внутри которого за счет эффекта Бернулли возникает кавитация. Пульсации неустойчивого вихря 2 возбуждают вертикальные изгибные колебания кольцевой струйной пластинки. Оптимальный режим гидродинамического звукообразования, при котором генерируется акустический сигнал максимального уровня, соответствует совпадению частоты пульсаций вихря с частотой основной гармоники колебаний кольцевой пластинки [4]. 

Кольцевая струйная пластинка характеризуется геометрическими параметрами: толщиной , шириной , внутренним радиусом  (радиус сопла) и внешним радиусом , причем толщина пластинки  мала по сравнению с радиусом  (рис. 1, б). Гидродинамическими параметрами струйной пластинки являются:  – плотность, модуль упругости затопленной струи и ее скорость на выходе из сопла. Расположим оси  и  в верхней плоскости кольцевой пластинки, ось  направим по нормали к этой плоскости, и декартову систему координат совместим с цилиндрической системой координат.  В первом приближении упругую струйную пластинку будем рассматривать как твердотельную пластинку с некоторым эквивалентным модулем упругости.

Для анализа вынужденных колебаний кольцевой пластинки воспользуемся неоднородным дифференциальным уравнением изгиба круглой пластинки в полярных координатах  [5]

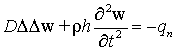                                                  ,                                            (1)

где – цилиндрическая жесткость круглой пластинки; – динамический прогиб пластинки; 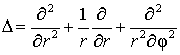 – оператор Лапласа;  – параметр времени; – интенсивность нормальной нагрузки (удельная внешняя сила, действующая в направлении нормали к поверхности круговой пластинки). Предполагаем, что кольцевая пластинка, деформируясь под действием сил, равномерно распределенных по ее внутренней поверхности, совер­шает только вертикальные изгибные гармонические колебания:

                    ; .                       (2)

Здесь  – удельные внешние силы, действующие в направлении соответствующих ортов цилиндрической системы координат;  – амплитуда удельной возбуждающей силы со стороны тороидального вихря;  – круговая частота вынужденных колебаний.

После подстановки выражений (2) в уравнение (1) и несложных преобразований данное уравнение примет вид

                                        ,                                 (3)

где – эквивалентная цилиндрическая жесткость струйной кольцевой пластинки, для ее вычисления используем формулу [3]

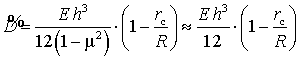                                       ,                           (4)

в ней  – модуль упругости струйной кольцевой пластинки, – коэффициент Пуассона. Для удобства вычислений перейдем от переменной  к приведенному расстоянию  и учтем, что  [3]. Тогда форма вынужденных колебаний кольцевой пластинки, функция , будет удовлетворять неоднородному дифференциальному уравнению

                                          ,                                  (5)

где 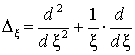, а для характеристического волнового числа  справедливо выражение

                                                                      .                                     (6)

Согласно предложенной модели считаем, что внутренний край струйной кольцевой пластинки  жестко защемлен, а на наружном крае  – отсутствуют продольное смещение, сдвиг и перерезывающие усилия. Поэтому граничные условия на контурах кольцевой пластинки имеют вид [3]:

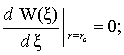
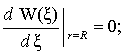
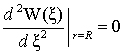                  .      (7)

Общее решение неоднородного уравнения (5) представляет собой сумму решения однородного уравнения и частного интеграла неоднородного уравнения:

                                              .                                               (8)

Причем решение соответствующего однородного уравнения имеет вид [3]:

      ,              (9)

где – функция Бесселя первого рода 0-го порядка;  – функция Бесселя второго рода 0-го порядка;  – модифицированная функция Бесселя первого рода 0-го порядка;  – модифицированная функция Бесселя второго рода 0-го порядка. Входящие в уравнение колебаний кольцевой пластинки параметры , где , являются корнями трансцендентного уравнения

                                                                                 (10)

При этом частоте основного тона (низшая гармоника) генерируемого акустического сигнала соответствует наименьший корень  [3].

Частным решением неоднородного уравнения (5) является постоянная функция . После подстановки этого значения в уравнение (5) получаем

                                                         .                                                        (11)

Итак, общее решение дифференциального уравнения вынужденных колебаний кольцевой струйной пластинки, с учетом (6), запишем в виде

 

                  .                 (12)

Используя граничные условия, определим неизвестные коэффициенты  и подставим их значения  в решение (12). Окончательно, для расчета амплитуды колебаний свободного края струйной пластинки  получим формулу:

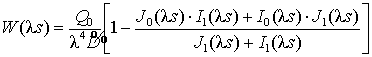                                    ,             (13)

где  – функция Бесселя первого рода 1-го порядка, – модифицированная функция Бесселя первого рода 1-го порядка.

В заключение отметим, что решение задачи вынужденных колебаний плоской осесимметричной струи позволяет рассчитывать на стадии проектирования амплитудно-частотные характеристики (АЧХ) жидкоструйных преобразователей с круговым щелевым соплом в виде соосных дисков.

Литература:

 

1.      Сухарьков О.В. Гидроакустическая излучающая рупорная антенна на основе  жидкоструйного преобразователя / О.В. Сухарьков // Акустичний вісник. – 2011. – 14, № 1. – С. 56 – 63.

2.      Сухарьков О.В. Передача дискретной информации в гидроакустический канал связи с использованием жидкоструйных преобразователей / О.В. Сухарьков // Цифрові технології. – 2011. – № 9. – С. 100 – 110.

3.      Сухарьков О.В. Модель жидкоструйного излучателя с круговым щелевым соплом в виде соосных дисков / О.В. Сухарьков // Наукові праці ОНАЗ ім. О.С. Попова. – 2011. – №2. – С. 107 – 113.

4.      Сухарьков О.В. Энергетические характеристики затопленной кольцевой струйной пластинки при наличии развитой кавитации / О.В. Сухарьков // Акустичний вісник. – 2010. – 13, № 2. – С. 45 – 52.

5.      Перцев А.К. Динамика оболочек и пластин / А.К. Перцев, Э.Г. Платонов. –           Л.: “Судостроение”, 1987. – 400 с.