Stochastic features of formation of a temperature field of preparation when grinding

Dyakonov A. A., Ermilov S.A.

South-Ural State University, Russia, Chelyabinsk

Occasional approach to thermal-physic task decision of grinding theory and numeral analysis based on imitation model realization by means of computer for the first time allow discovering the number of physical particular qualities of temperature field blank formation in this process.

The fig. 1 illustrates, there is the contact length at the axis of absciss and there is the grinding width at the axis of ordinates. It allows to monitor the nature of temperature field formation in the contact zone both in the cutting moment by grains (maximal temperature tops) and in the «rest» time until the next grain enters when the material is getting cold. At the graphs you can see the critical fluctuation points of temperature field – maximal and minimal temperature. Furthermore, the temperature field has the not stational and irregular character both at the contact length and the contact width, in other words the temperature fluctuations move to the area of higher temperature at time.

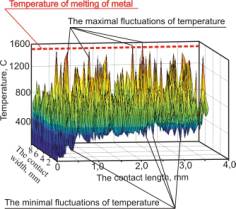
Fig. 1. The temperature field blank kind by grinding

For the all materials the maximal temperatures could reach and even exceed melting-point and independently on processing kind. It is the demonstration of one assumption influence using in thermal-physics model, namely metal – isotope and while calculating its phase transformations during heat spread process (latent warmth melting) are not taken into account. It allows avoiding nonlinear thermal conductivity differential equation. It is very important to solve this problem for investigations those concerned with determination of structural changes in the surface layers. This problem is not discussed in the present report. Moreover, A.A. Koshin [1] represents that material melting temperature is available only on the surface, and in the significant volumes of surface layers determining the quality of processing this effect is not monitored.

Thus, the maximal temperature that appears in the thin surface layers, could reach physically the melting-point and since this time the getting cold happens whish is describing in the designed thermal-physics model.

The particular cases are recognized after analyzing the great number of temperature field diagrams. So, for the all examined material marks independently on the grinding kind, the sudden increases and drops interchange in the temperature of getting cold is monitored in the high temperature zone. It is concerned with nonlinear changes of dependence “Solidity-Temperature” for that diapason in which the meanings of material solid characteristics (σ_i) and intensity heat sources (q) are not taking into account.

Comparing the given temperature fields for different kinds of grindings it could be established that while the contact length increases the temperature gradient increases too. So, during the round outside grinding of carbon steels the average temperature gradient is 380 °C, during the flat grinding – 650 °C and during the internal grinding – 310 °C.

On the other hand, the temperature increase is not proportionate to contact length increase as correlation of the contact length at flat and outside round grinding at average technological conditions is 3,8 : 1, and correlation of temperature is 1,7 : 1. This event could be explained by availability of acceleration and stabilization zone (fig. 2) at temperature field. The drastic temperature increase that practically equals the maximal temperature happens on the contact length that is 1 mm not dependently on grinding kind, and the future development of temperature field happens at stabilization dependence relatively to abscissa axis. However the part of acceleration zone of the contact length for every kind is not similar, for example, for the round outside grinding it is 100%, for the internal grinding – 62%, for the flat grinding – 25%.

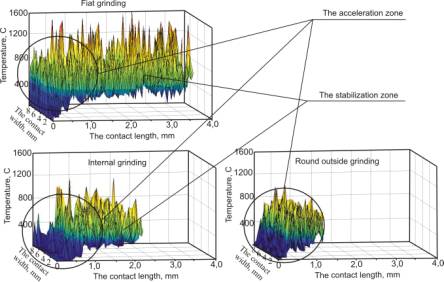
Fig. 2. Characteristic sites of temperature field blank formation

Consequently the temperature field blank by grinding possesses of two criteria zones: the zone of drastic temperature increase (the acceleration zone) and the stabilization zone.

Modification of the given diagrams into the line level diagrams (fig.3) allows to monitor distribution and heterogeneity of temperature field blank in the contact zone.

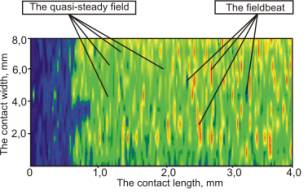
Fig. 3. The line level heterogeneity diagram of temperature field blank

in the contact zone by grinding

Fig. 2 illustrates quasi-stationary temperature field is created in the results of the frequent influence of abrasive grains on the stabilization zone that is 800 ºС, due to occasional grinding process temperature pulsation happens in the interval of 200–1400 ºС.

The main particular quality of temperature field, which was idealized vastly by investigators [2], is occasional character of its formation. Starting from this, to evaluate temperature field in the contact zone the application of mathematical statistics is required as the average of temperature in this case, obviously disfigures the real situation.

Two central moments of mathematical statistics are implemented for evaluation:

M (U) – mathematical temperature waiting in the considered interval at the contact length;

R(U) – swing of temperature relatively to mathematical waiting in the considered interval at the contact length.

Two-parameter evaluation system was realized by computer statistics prognostication STATISTICA 6.0. To determine mathematical waiting M (U) and swing R (U) in every interval at the contact length the meanings of temperature at the contact width included in this interval are considered.

The example of trusting temperature field evaluation at flat grinding of AISI304 is illustrated on the fig. 4. The results confirm the necessity of two-parameter evaluation system as the swing in the dependence on the considered contact length could obtain 220–980ºС. The analyzing of the graphs allows concluding that temperature field blank possesses additional particular qualities besides indicated earlier.

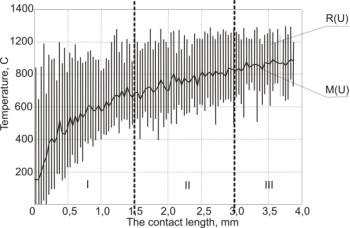
Fig. 4. The temperature swing interval statistics

The temperature swing obtains the different meanings on the individual contact length in which connection its meaning decreases while the contact length increases.

The temperature swing interval statistics

The grinding kind	Number of the site
	I	II	III
	R (U), ^0С
Round outside	530	500	421
Internal	550	390	–
Flat	560	421	320

Conclusion

Occasional approach to thermal-physic task decision of grinding theory and numeral analysis based on imitation model realization by means of computer for the first time allow discovering the number of physical particular qualities of temperature field blank formation in this process.

It was established that temperature field has quasi-stationary occasional character.

It was discovered that availability of two criteria zones – the acceleration zone was defined by drastic temperature increase and the stabilization zone was conformed by constant level of temperature field formation – is typical for temperature field in the contact zone by grinding.

The statistic characteristics – two central moments of mathematical statistics: the mathematical waiting M(U) and the swing R(U) are offered for numeral evaluation of temperature field blank in the grinding zone.

References

1. Koshin A.A. Research of physical communications at grinding // The Processing of metals. Novosibirsk, 1997. №1. P. 22–25.

2. Korchak S.N. Productivity of process of grinding of steel details. M.: Mechanical engineering, 1974. 280 p.