Сельское хозяйство/2. Механизация сельского хозяйства

К.т.н. Пархоменко Г.Г., инженер Божко И.В.

Государственное научное учреждение Северо-Кавказский Научно Исследовательский Институт Механизации и Электрификации Сельского Хозяйства Россельхозакадемии

Результаты оптимизации формы почвообрабатывающих рабочих органов

Рабочие органы для обработки почвы должны обеспечивать выполнение качественных показателей технологического процесса с min затратами энергии. Это достигается при оптимизированных форме и параметрах рабочих органов.

С точки зрения физической математики [1], эллипс является наилучшей кривой, обладающей свойством min. Если рассмотреть две точки (А и В) в поперечно-вертикальной плоскости, определяющие min ширину захвата (b) разработанного рабочего органа, лежащие на поверхности поля, предполагаемого топографически гладким на макроуровне, и горизонтальную прямую Х, ограничивающую глубину обработки (a), можно на данной прямой отыскать такую точку (), чтобы сумма,была постоянно наименьшей, т.е. (рисунок 1).

В физической математике [1] подобная задача рассматривается с помощью линий уровня; придается степень подвижности точки, перемещающейся свободно в поперечно-вертикальной плоскости при соблюдении приведенного выше условия. Решением данной задачи является траектория движения точки в виде эллипса с фокусами в точках А и В. Искомый min образуется при пересечении эллипса с прямой X (рисунок 1).

Данное решение не противоречит самому определению эллипса, который представляет собой геометрическое место точек, сумма расстояний которых до двух данных точек А и В имеет одно и то же значение, т.е. const [2].

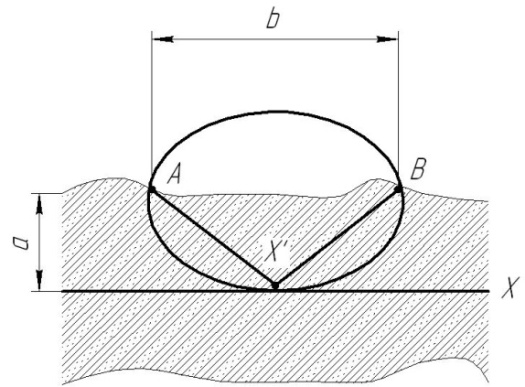
Рисунок 1 – Эллипс с точки зрения физической математики.

АВ – фокусное расстояние, представляет собой min ширину захвата рабочего органа. Линии уровня – это конфокальные [1] эллипсы, т.е. с одними и теми же фокусами (А и В).

Таким образом, наилучшей кривой обладающей свойством min в данных условиях является эллипс. В связи с этим придав рабочему органу форму эллипса, мы обеспечиваем обработку пласта почвы от поверхности поля до заданной глубины с высокой степенью крошения и min затратами энергии.

Известное свойство эллипса [2] о сходимости лучей после отражения из одного фокуса в другом по аналогии можно применить к обработке почвы, так поток почвы при движении агрегата, отталкиваясь при соударении о поверхность рабочего органа перемещается из одного фокуса эллипса в другой. При этом наблюдается дополнительное крошение и некоторая сепарация слоя с вынесением на поверхность более прочных макроагрегатов почвы и просыпанием в щели между ними эрозионно-опасных частиц, которые остаются внутри пласта.

Для уменьшения силы резания пласта целесообразно представить разрабатываемый рабочий орган в виде кольца с формой эллипса, образованного равномерным сжатием окружности, с параметром соответствующим углу сдвига почвы в продольно-вертикальной плоскости.

Параметр (коэффициент сжатия) эллипса можно определить по формуле, выведенной на основании теории прочности Мора:

(1)

где β – угол крошения (установки режущей грани), φ – угол внешнего трения рабочего органа о почву, ρ – угол внутреннего трения почвы о почву.

Интенсивность возникающих на поверхности кольцевого рабочего органа напряжений можно оценить, рассмотрев задачу о внутреннем трещине эллиптической формы, расположенной в бесконечно протяженном сплошном теле под действием нагрузки. Для решения этой задачи в механике разрушения [3] А. Грин и И. Снеддон [4], а также Г. Ирвин [5] получили коэффициент интенсивности напряжений, с увеличением которого можно объективно судить об увеличении нагрузки на поверхность эллипса:

(2)

где - требуемая глубина обработки почвы эллиптическим рабочим органом.

Формула (2) представляет выражение для определения коэффициента интенсивности напряжений, возникающих по периметру пласта почвы эллиптической конфигурации при взаимодействии с кольцевым рабочим органом.

Полученная зависимость (2) графически представлена на рисунке 2 для различных углов крошения (, и ).

В качестве исходных данных напряжение принято равным временному сопротивлению сжатия глинистого чернозема, которое для засушливых условий составляет 93 – 98 кПа.

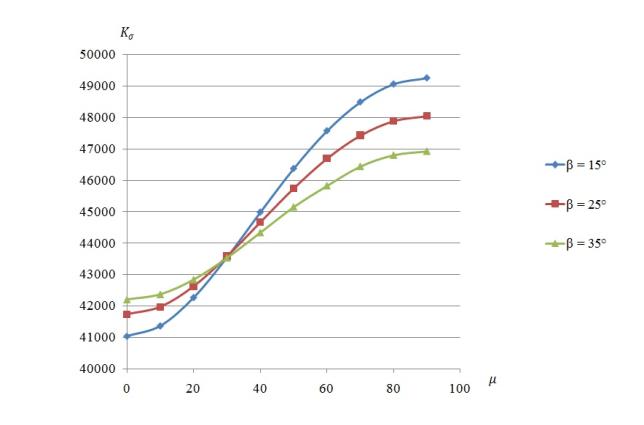
Рисунок 2 – Зависимость коэффициента интенсивности напряжений по

периметру эллипса от параметров рабочего органа

Анализ графика свидетельствует о том, что наибольшая интенсивность напряжений локализована на концах малой оси эллипса (), а наименьшая – на концах большой оси (). Причем рост интенсивности напряжений неравномерный: наибольший приходиться на область , наименьший при , . С увеличением угла крошения интенсивность напряжений увеличивается до , а далее снижается, что объясняется изменением коэффициента сжатия (параметра) эллипса, который зависит от угла и определяет соотношение малой и большой осей эллипса.

Анализ графика (рисунок 2) показывает, что наибольшая интенсивность напряжений возникает в области расположения горизонтальных режущих кромок рабочего органа, что следует учитывать при прочностных расчетах, поскольку неравномерность нагрузки способствует локальному износу кольца в указанной зоне. При этом переменная интенсивность напряжений по контуру пласта приводит к возникновению разнонаправленных деформаций (растяжения и сжатия), что благоприятно сказывается на качестве крошения и способствует снижению затрат энергии на обработку почвы кольцевым рабочим органом.

Литература:

1. Пойа, Д. Математика и правдоподобные рассуждения / Д. Пойа – М.: Наука, 1975 – 464 с.

2. Выгодский, М.Я. Справочник по высшей математике / М.Я. Выгодский – М.: Физматгиз, 1963 – 872 с.

3. Броек, Д. Основы механики разрушения / Д.Броек – М.: Высшая школа, 1980 – 368 с.

4. Green, A.E. Nye stress distribution in the neighborhood of a flat elliptical crack in an elastic solid / A.E. Green, I.N. Sneddon // Proc. Cambridge Phil Soc. – 1950 – 46 – p.p. 159 – 164.

5. Irwin, G.R. The crack extension force for a part – through crack in a plate / G.R. Irwin // Trans. ASME. J. Appl. Mech. – 1962 – p.p. 651 – 654.