Сельское хозяйство
Ктн. Патрин В.А., ктн Патрин А.В.
Новосибирский государственный аграрный университет,
Россия
Энергодинамика плоских колеблющихся решёт сортировальных машин
Предложен новый
синергетический метод описания поведения зерновой среды на плоских колеблющихся
решётах. Получены три уравнения, позволяющие, моделировать процесс передачи
энергии от поверхности решета в зерновую среду и образование потенциальной и
свободной энергии в обрабатываемом зерне.
Доказано, что
система «плоское решето – обрабатываемое зерно» обладает элементами
самоорганизации, за один полупериод колебания имеет четыре сменяющих друг друга
режима движения зерна.
Получена
зависимость времени полупериода колебания и ускорения силы инерции от угловой
скорости привода плоского решета. Предложены направления совершенствования
плоских решёт.
Ключевые слова: плоское решето, зерновая среда, энергодинамика системы «решето –
обрабатываемое зерно».
Определение закономерностей взаимодействия
обрабатываемого зерна с рабочими органами сортировальных машин представляет
сложную задачу, которая не решается существующими методами классической
механики, поэтому теория процесса сепарации зерна сводилась к изучению движения
материальной точки по поверхности рабочего органа.
Любой рабочий орган сортировальных машин и
обрабатываемая сыпучая среда представляет собой открытую нелинейную
диссипативную систему с элементами самоорганизации и авторегулирования.
Поведение сыпучей среды подобно поведению
плазмы, жидкости и атмосферным явлениям.
При незначительном изменении управляющих
параметров в сыпучей среде появляются новые структурные образования, новые виды
движения частиц, новые фазовые состояния сыпучей среды, объяснить которые с
позиции классической механики затруднительно.
На плоских колеблющихся решётах Блехман
[1] классифицировал семь регулярных режимов движения зерна. В цилиндрических
решётах авторами зафиксировано семь устойчивых видов движения и фазовых
состояний зерновой среды, переходящих из одного вида в другой при изменении
управляющего параметра [2].
В синергетике используется понятие
«детерминированного хаоса», где нелинейные системы на локальных промежутках
времени являются устойчивыми равновесными, а на более длительных участках
проявляют неустойчивость, обострение порядка, хаос, которые в точках бифуркаций
сменяются новым порядком.
Эдвард Лоренц составил систему уравнений,
описывающих атмосферные явления, которые оказались пригодными и для описания
течения жидкости в ячейках Бинара [3].
Авторами получена система уравнений,
соответствующая правилам синергетики для описания взаимодействия зерновой среды
с плоскими решётами [4]
Евш→П→Евн= F + ST, (1)
Евн = ( аw – вw2)·Кн, (2)
Fд = Fj – Fс, (3)
где Евш
– внешняя кинетическая энергия, передаваемая решетом в систему; П – потенциальная энергия зерна, переходящая
в кинетическую энергию зерна Евн; F – свободная энергия, направленная на перемещение зерна; ST = Q – энтропия, или тепловые потери в результате трения и
остаточной деформации зерна; w – угловая скорость привода решета; а, в – коэффициенты учитывающие интенсивность поступления энергии в
зерновую среду; Кн – коэффициент,
учитывающий нагрузку зерна на решето; Fд – движущая сила;
Fj – сила инерции; FC – сила сопротивления зерна сдвигу.
Цель настоящей работы заключается
в проведении качественного анализа полученной системы уравнений для определения
оптимальных режимов работы плоских колеблющихся решёт.
Методика и результаты
теоретического исследования.
Первое уравнение системы (1) показывает
направление перехода и трансформацию энергии в системе.
Анализ показал, что внешняя энергия Евш у всех рабочих органов
сортировальных машин переходит во внутреннюю кинетическую энергию зерновой
среды Евн через обязательное накопление потенциальной энергии П. Правая часть данного уравнения
представляет термодинамический потенциал Гельмгольца. Количество свободной
энергии определяет порядок системы, в который входит структура сыпучей среды,
вид движения, устойчивость траекторий частиц и т.д. Свободная энергия и
энтропия являются конкурентными, увеличение одного, ведёт к уменьшению другого
вида энергии. Управляющим параметром системы, определяющим количество свободной
энергии в обрабатываемом зерне, является кинематический режим решета (угловая
скорость кривошипа) и величина нагрузки зерна на решето.
Закономерность поступления энергии в
зерновую среду от поверхности рабочего органа определяется уравнением (2).
Данное уравнение отражает процесс самоорганизации системы и взаимодействие её с
внешней средой. Вывод уравнения дан в работе авторов [2].
На первом этапе функционирования системы
увеличение угловой скорости (аw) повышает
количество свободной энергии в зерне, на втором этапе отрицательная величина (–вw2) обеспечивает обратную связь в саморегулирующейся
системе и снижает количество энергии, поступающей в зерновую среду. Физический
смысл данного явления основан на противоречии: Чем больше разрыхляется
(псевдоожижается) сыпучая среда, тем больше она теряет связь между частицами
зерновой среды и между зерновым телом и поверхностью решета. При этом
уменьшаются силы трения, следовательно, уменьшается и количество передаваемой
энергии от решета зерновой среде, снижается интенсивность сепарации. Возникает
тупиковая ситуация, чтобы интенсифицировать процесс сепарации необходимо больше
сообщить энергии частицам сыпучей среды, в то же время увеличение скорости (w) рабочего органа поступление энергии в зерно с
определённого момента начинает уменьшаться.
Третье уравнение системы (3) по правилам
синергетики составляется из условия равновесия действующих сил и сил
сопротивления движению. Тот или иной порядок в системе зависит от величины
силового поля, в котором находится зерновая среда. В нашем случае это
переменное поле состоит из векторных величин ускорения силы тяжести и силы
инерции.
Движущей силой является результирующая
двух сил, активной силы инерции Fj и силы сопротивления сдвигу Fс
элементарного слоя. Если принять массу m = 1, то удельная сила сопротивления сдвигу любого
элементарного слоя по наклонному решету определится как приведённый коэффициент
трения [1]:
вниз – fпр.н= f0н(1 + 2εi); (4)
вверх – fпр.в= f0в(1 + 2εi), (5)
где f0н – удельное сопротивление сдвигу верхнего слоя вниз по
решету
f0н = sin(φ – α) / cos(α – φ); (6)
f0в –
удельное сопротивление сдвигу верхнего слоя вверх по решету
f0в = tg(α + φ); (7)
где
α
– угол наклона решета; φ – угол трения зерна по решету; i = h/н –
безразмерная координата рассматриваемого слоя зерна, лежащего на глубине h при толщине зерна н на решете: ε
– коэффициент, характеризующий физико-механические свойства зерна ε
= (0,156 ÷ 0,215).
Ускорение решета, при
котором начинает сдвигаться элементарный слой:
w12А = gfпр.н – вниз по
решету; (8)
w22А = gfпр.в – вверх по
решету; (9)
Авторами разработана
имитационно-графическая модель для исследования режимов движения зерна на
плоском решете [4], в которой за один полупериод колебания решета
последовательно сменяются четыре фазы движения: относительный покой зерна на
решете, послойное сдвиговое течение с отставанием от нижнего слоя, свободное
перемещение зернового тела относительно поверхности решета, послойное сдвиговое
течение с опережением нижнего слоя.
Каждое
фазовое состояние зерна на поверхности плоского решета выполняет свою функцию в
процессе сепарации.
Фаза относительного покоя зерна на решете
необходима для накопления потенциальной энергии. Энергия переносного движения
решета переходит в потенциальную энергию массы зерна, находящегося так же, как
и решето в переносном движении.
Две фазы относительного сдвигового течения
элементарных слоёв зерна внутри
зернового тела обеспечивают разрыхление (псевдоожижение) сыпучей среды, во
время которого мелкие частицы перемещаются к поверхности решета.
Фаза относительного перемещения сыпучей
среды как «твёрдого» тела по поверхности решета необходима для прохождения
частиц через отверстия решета и удаления полученных фракций из машины.
Во всех перечисленных фазовых состояниях
обрабатываемого зерна наблюдается когерентное (согласованное) поведение множества
частиц. Обоснование согласованности поведения частиц на микроуровне дано
авторами в работе [4]. Таким образом невыполнение любой фазы движения зерна из
перечисленных выше приведёт к нарушению процесса сепарации, разрушению системы.
Важно оценить время в течении которого совершается полный цикл смены фаз
движения зерна и определить его зависимость от угловой скорости.
При гармонических колебаниях плоского
решета ускорение j и сила инерции определяются из уравнений
j = –Аw2sinwt; (10)
Fj = mАw2sinwt,
где
А – амплитуда колебаний; w – угловая скорость; wt – угол поворота кривошипа.
Максимальные значения
ускорения и силы инерции определяются
jmax = –Аw2; Fj = mАw2. (11)
Время полупериода колебания Т/2 = π/w. (12)
Используя выражения (11) и (12) построим
график зависимости времени полупериода колебания Т/2 и ускорения jmax от угловой скорости
кривошипа решета.
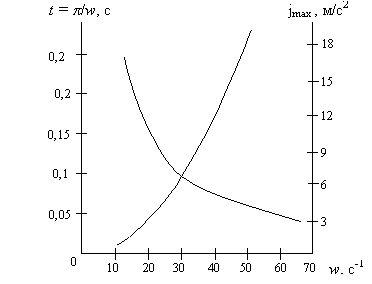

Рисунок 1. Зависимость времени полупериода колебания и
ускорения плоского решета от угловой скорости кривошипа при А = 7,5 мм.
Приведём кинематику
решётных станов зерноочистительных машин
|
Марка |
Обороты, частота колебаний, n, мин-1 |
Амплитуда колебаний решёт, А, мм |
|
Ускорение j = Аw2, м/с2 |
Время полупериода колебания t = π/w, c |
|
ОВС-25
|
460 |
7,5 |
48 |
17,28 |
0,065 |
|
СМ-4 |
418 |
7,5 |
43,75 |
14,3 |
0,07 |
|
ЗАВ-10.30000 |
440 |
7,5 |
46,05 |
15,87 |
0,068 |
|
ЗСМ-20 |
500 |
5,0 |
52,3 |
13,7 |
0,06 |
Из таблицы и графика видно, что время
полупериода колебания в реальных машинах составляет всего 0,06 – 0,08 с.
За это время сыпучая среда должна пройти
все четыре перечисленных выше фазовых состояний необходимых для сепарации.
Слабым звеном плоских решёт с
горизонтальными колебаниями является снижение количества передаваемой энергии
от решета в обрабатываемое зерно. Данное явление можно сравнить с «буксованием»
решета относительно зерна и проскальзывание одного элементарного слоя
относительно другого. По мнению авторов теоретически выйти из данной ситуации
можно:
а) Не изменяя величину ускорения и силы
инерции можно уменьшить угловую скорость, увеличив, при этом, амплитуду
колебаний решета;
б) Увеличить шероховатость поверхности
решёт. В процессе работы поверхность решета шлифуется зерном, усугубляя процесс
сепарации.
в) Работу решета вести при максимально
допустимой толщине зерна на решете при которой увеличивается нормальное
давление и силы трения относительно решета и между зёрнами.
Почему вибрационные решёта работают
успешно при колебаниях на порядок выше, чем решёта с горизонтальными
колебаниями? Теоретически это объясняется разными способами передачи энергии
зерну. В первом случае энергия от поверхности решета передаётся за счёт удара
(импульса силы). Сила импульса почти перпендикулярна зерновому «телу» и время
её действия на зерно не играет большой роли. В колеблющихся решётах передача
энергии зерну осуществляется силами трения.
Экспериментальные исследования показали,
что передача движения силами трения заканчивается на пятом–шестом слое сыпучей
среды. При работе вибрационных решёт передача движения частицам от импульса
силы (ударом) распространяется на толщину слоя зерна 4-5 см. Дальше энергия
рабочего органа не передаётся, гасится в поровых промежутках между частицами
зерновой среды.
Выводы:
1. Полученные авторами синергетические
уравнения достоверно описывают динамику перехода внешней энергии в
обрабатываемую зерновую среду на плоских колеблющихся решётах.
2. Тот или иной порядок в системе (структура,
вид движения зерна и его фазовое состояние) определяется количеством свободной
энергии переданной поверхностью решета зерну. Условия передачи энергии зерну
зависят от угловой скорости решета и ускорения силы тяжести.
3. Время полупериода колебания решета, в
течении которого зерновая среда должна пройти полный цикл с меняющихся
поочерёдно четырёх фаз движения, необходимых для процесса сепарации у
существующих сортировальных машин составляет всего 0,06 – 0,07 с, что по мнению
авторов является недостаточным.
4. Повысить удельную производительность
плоских решёт можно за счёт увеличения амплитуды колебания решета, нагрузки
зерна на решете, увеличения коэффициента трения зерна по поверхности решета при
снижении оборотов привода решета.
Литература:
1. Гортинский В.В. Процессы сепарирования
на зерноперерабатывающих предприятиях / В.В. Гортинский, А.Б. Демской, М.А.
Борискин. – М.: Колос, 1980. – 303с.
2. Патрин В.А. Моделирование динамики
взаимодействия зерновой среды и рабочих органов сортировальных машин / В.А.
Патрин, В.А. Крум, А.В. Патрин. // Механизация и электрификация сельского
хозяйства. – 2013. №2. – С. 4-7.
3. Данилов Ю.А. Лекции по нелинейной
динамики / М.: Либроком, 2011. – С. 56-62.
4. Патрин В.А. Синергетическая теория
взаимодействия зерновой среды с плоскими решётами // Механизация и электрификация
сельского хозяйства. – 2013. №4. – С. 26–29.

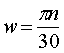 , с
, с