Современные информационные технологии /1. Компьютерная инженерия

К.т.н. Аждер Т.Б.

Московский государственный университет приборостроения и информатики

ПРИНЦИП РАЦИОНАЛЬНОСТИ ПРИ ОПРЕДЕЛЕНИИ СЛОЖНЫХ РЕШЕНИЙ

При обучении часто возникают ситуации, связанные с неполной информацией, например, когда знаний обучаемого недостаточно для того, чтобы построить объяснение и/или доказательство некоторого наблюдаемого факта.

Допустим, есть некоторый простой набор наблюдаемых данных, набор правил, которые легко можно проверить, не используя дополнительных технических средств. На основе конкуренции гипотез найдем ту гипотезу, которая наилучшим образом сможет объяснить наблюдаемых данных.

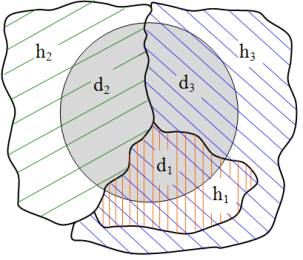
Рисунок 1. Пример покрытия трех элементов данных тремя гипотезами

Условия задачи изображены на рисунке 1. Здесь имеется:

– набор из трех элементов наблюдаемых данных D = (1, 1, 0);

– набор из трех объяснительных гипотез

h₀ = (1, 0, 1), h₁ = (0, 1, 1), h₂ = (1, 0, 0).

Результатом работы алгоритма конкуренции гипотез при решении данной задачи будет следующий график зависимости значений конкурирующих гипотез от времени (итераций).

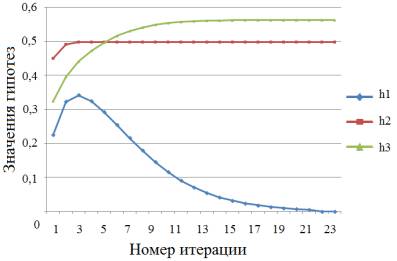
Рисунок 2. Диаграмма зависимости значений гипотез от времени

Из диаграммы видно, как гипотеза h₁ затухает и принимает значение, стремящееся к нулю, в то время как гипотезы h₂ и h₃ стабилизируются в значениях, отличных от нуля. Принимая наибольшее значение среди рассматриваемых гипотез, h₃ является явным победителем и признается лучшим объяснением наблюдаемых данных. Гипотеза h₂ в условиях задачи определяется как неполная. Результаты диаграммы показывают, как алгоритм выявляет ложные или неполные гипотезы и повышает значение правильной, соответствующей гипотезы.

Апробация данной методики позволяется сделать вывод, что данную модель можно использовать только для решения простых задач, когда одна гипотеза независимо от других может полностью объяснить наблюдаемые данные. Если же рассматривается более сложный случай, когда одной гипотезой можно объяснить лишь часть данных, то полученное при работе данной модели решение не предполагается 100%-ого объяснения рассматриваемых данных и априори является неполной гипотезой. В этом случае необходимо применить алгоритм поиска рационального решения.

Синтез сложных объяснений, т.е. определение составных гипотез, необходим при решении задач, когда в базе нет той элементарной гипотезы, которая была бы единственным решением поставленной задачи. В этом случае необходимо определить множество простых гипотез, каждая из которых будет объяснять одну часть наблюдаемых данных, и синтезировать из них сложное объяснение, объясняющее наблюдения полностью.

Для выделения рационального решения задачи необходимо, во-первых, исследовать возможные наборы элементарных гипотез на степень их объяснения наблюдаемых данных, а, во-вторых, учесть количество этих гипотез, или компонент, в итоговом решении. Формула вычисления значения составной гипотезы выглядит следующим образом:

.

Первое слагаемое представляет собой количество элементов составной гипотезы, а второе слагаемое – значение покрытия данных, принимающее значение нуля в случае полного покрытия данных.

Подставив данные рассмотренного выше примера в формулу вычисления S_k, получим следующие результаты:

Hck	h1	h2	h3	h1,h2	h1,h3	h2,h3	h1,h2,h3
Sk	5	4	3	3	3	2	3

Из всех возможных вариантов включения элементарных гипотез в сложную, минимальное значение S_k соответствует гипотезе H_c6=(h₂, h₃), которая в данных условиях задачи является рациональным решением.

Значение покрытия данных при H_c6=(h₂, h₃) равно нулю. Это говорит о том, что данное решение дает возможность полностью объяснить все элементы наблюдаемых данных, используя для этого 2 элементарные гипотезы.

Литература:

1. Вагин В.Н., Головина Е.Ю., Загорянская А.А., Фомина М.Б. Достоверный и правдоподобный вывод в интеллектуальных системах / В.Н. Вагин, Е.Ю.Головина, А.А. Загорянская, М.Б. Фомина. – М.: Физматлит, 2004.

2. Люгер Дж. Ф. Искусственный интеллект: стратегии и методы решения сложных проблем, 4-е издание. Пер. с англ. – М.: Издательский дом "Вильямс", 2005.

3. Кулик Б.А. Логика естественных рассуждений / Б.А. Кулик. – СПб.: Невский диалект, 2001.