К.т.н. Данилова Ю.С.
Поволжский государственный
университет сервиса, Россия
Использование коммутирования функций
при решении простейших функциональных уравнений
Композицией
отображений ![]() и
и ![]() называется отображение
называется отображение ![]() , которое действует по правилу
, которое действует по правилу ![]() . Отображения
. Отображения ![]() и
и ![]() называются коммутирующимися (перестановочными), если
называются коммутирующимися (перестановочными), если ![]() .
.
По всякому отображению ![]() можно построить
последовательность отображений
можно построить
последовательность отображений ![]() посредством следующей
реккурсивной процедуры:
посредством следующей
реккурсивной процедуры: ![]() . Отображение
. Отображение ![]() называется итерацией
порядка
называется итерацией
порядка ![]() отображения
отображения ![]() . Любые две итерации одного и того же отображения
коммутируют:
. Любые две итерации одного и того же отображения
коммутируют: ![]() . Более того, если некоторые отображения
. Более того, если некоторые отображения ![]() и
и ![]() перестановочны, то
перестановочны и любые их итерации
перестановочны, то
перестановочны и любые их итерации ![]() и
и ![]() [1].
[1].
Точка ![]() называется
неподвижной точкой отображения
называется
неподвижной точкой отображения ![]() , если
, если ![]() . Если каждая точка области определения
. Если каждая точка области определения ![]() некоторого отображения является его неподвижной точкой, то
такое отображение называется тождественным и обозначается через
некоторого отображения является его неподвижной точкой, то
такое отображение называется тождественным и обозначается через ![]() .
.
Если в
последовательности итераций ![]() встречается
тождественное отображение, то такая последовательность итераций оказывается
периодической, а отображение
встречается
тождественное отображение, то такая последовательность итераций оказывается
периодической, а отображение ![]() называется циклическим.
называется циклическим.
В связи с введенными
общими понятиями множества и отображения могут быть совершенно произвольной
природы.
Начиная с этого места
под множествами подразумеваются некоторые подмножества R или C, а под отображениями –
числовые функции. Вот некоторые конкретные примеры определенных на R коммутирующих функций:
а) ![]() и
и ![]() ; б)
; б) ![]() и
и ![]() .
.
Отметим, что пресловутые
нечетные функции – это в точности те функции, которые коммутируют с линейной
функцией ![]() . А вот скажем, функции, которые можно представить в виде
суммы тождественной и периодической ( с
периодом b) функций.
. А вот скажем, функции, которые можно представить в виде
суммы тождественной и периодической ( с
периодом b) функций.
Если в формальном
равенстве ![]() конкретно фиксировать
функцию g, то возникает функциональное
уравнение (относительно неизвестноцй функции f ), общее решение которого – это совокупность всех тех функций, что
коммутируют с g.
конкретно фиксировать
функцию g, то возникает функциональное
уравнение (относительно неизвестноцй функции f ), общее решение которого – это совокупность всех тех функций, что
коммутируют с g.
Сразу же укажем на
несложный первичный арсенал технических средств для получения результатов в
рассматриваемом круге вопросов [2]:
1)
метод неопределенных коэффициентов;
2)
удачное введение новой неизвестной функции или новой
переменной;
3)
переход от равенства вида ![]() к равенству с
итерациями
к равенству с
итерациями ![]() (возможно с
последующим предельным переходом).
(возможно с
последующим предельным переходом).
Рассмотрим детально
именно такую задачу ![]() в класссе непрерывных
на R функций для случая, когда известная
функция g является линейной, включив её в
следующую несколько более широкую задачу: при заданных
в класссе непрерывных
на R функций для случая, когда известная
функция g является линейной, включив её в
следующую несколько более широкую задачу: при заданных ![]() найти все непрерывные
на R
функции, удовлетворяющие тождеству:
найти все непрерывные
на R
функции, удовлетворяющие тождеству: ![]() (1).
(1).
Для решения уравнения
(1) рассмотрим три случая:1)![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
Для удобства решения
через S обозначим множество всех функций
определенных и непрерывных на луче ![]() . Через Т –
множество всех функций непрерывных и периодических на R , для которых единица является одним из периодов.
Через
. Через Т –
множество всех функций непрерывных и периодических на R , для которых единица является одним из периодов.
Через ![]() и
и ![]() обозначим совокупности
всех тех функций из S и Т соответственно, которые в нуле обращаются в ноль.
обозначим совокупности
всех тех функций из S и Т соответственно, которые в нуле обращаются в ноль.
Случай 1: ![]() . Функциональное уравнение приобретает вид
. Функциональное уравнение приобретает вид ![]() (2).
(2).
Если ![]() , то замена
, то замена ![]() приводит уравнение (2) к виду
приводит уравнение (2) к виду ![]() и, следовательно,
общее решение описывается формулой
и, следовательно,
общее решение описывается формулой ![]() , где
, где ![]() . Если
. Если ![]() и
и ![]() , то замена
, то замена ![]() приводит уравнение
(2) к виду
приводит уравнение
(2) к виду ![]() и, следовательно, общее решение описывается формулой
и, следовательно, общее решение описывается формулой ![]() , где
, где ![]() . Если, наконец,
. Если, наконец, ![]() , то замена
, то замена ![]() приводит уравнение
(2) к виду
приводит уравнение
(2) к виду ![]() . В этом случае
. В этом случае ![]() , множество М корней уравнения
, множество М корней уравнения ![]() не пусто и пусть
не пусто и пусть ![]() . Ясно, что
. Ясно, что ![]() .
.
Функция ![]() является непрерывной,
периодической и удовлетворяющей условию
является непрерывной,
периодической и удовлетворяющей условию ![]() . В таком случае общее решение описывается формулой
. В таком случае общее решение описывается формулой
![]() , где
, где ![]() и
и ![]() .
.
Случай 2: ![]() , Функциональное уравнение приобретает вид
, Функциональное уравнение приобретает вид ![]() (3).
(3).
Из тождества ![]() следует, что
следует, что ![]() для любого
для любого ![]() . Следовательно, при
. Следовательно, при ![]() имеется единственное
решение
имеется единственное
решение ![]() уравнения (3), а при
уравнения (3), а при ![]() решение может
существовать лишь при условии, что
решение может
существовать лишь при условии, что ![]() . В этом случае
. В этом случае ![]() замены
замены ![]() и
и ![]() приводит уравнение
(3) к тождеству
приводит уравнение
(3) к тождеству ![]() . Обозначим через
. Обозначим через ![]() сужение
сужение ![]() на
на ![]() . Тогда очевидно
. Тогда очевидно ![]() и так, кстати,
утроена всякая чётная непрерывная функция. А всякая чётная целая (аналитическая
на всей плоскости С) функция
и так, кстати,
утроена всякая чётная непрерывная функция. А всякая чётная целая (аналитическая
на всей плоскости С) функция ![]() устроена так:
устроена так: ![]() , где h – некоторая целая
функция. Это получается рассуждением на основе метода неопределенных
коэффициентов:
, где h – некоторая целая
функция. Это получается рассуждением на основе метода неопределенных
коэффициентов:
![]() . Итак, в этом случае общее решение описывается формулой
. Итак, в этом случае общее решение описывается формулой ![]() , где
, где ![]() .
.
И наконец, если ![]() , то посредством замен
, то посредством замен ![]() и
и ![]() уравнение (3)
приводится к тождеству
уравнение (3)
приводится к тождеству ![]() . Обозначим через
. Обозначим через ![]() сужение
сужение ![]() на
на ![]() . Тогда
. Тогда ![]() и так, между прочим устроена всякая нечетная непрерывная
функция. Таким образом, в этом последнем случае общее решение описывается
формулой
и так, между прочим устроена всякая нечетная непрерывная
функция. Таким образом, в этом последнем случае общее решение описывается
формулой ![]() , где
, где ![]() .
.
Случай 3. ![]() .
.
Замены ![]() и
и ![]() приводят уравнение
(1) к виду
приводят уравнение
(1) к виду ![]() .
.
В таком случае, ![]() . Если
. Если ![]() , то посредством замены
, то посредством замены ![]() можно перейти от (4)
к уравнению
можно перейти от (4)
к уравнению ![]() , где
, где ![]() . При
. При ![]() замены
замены ![]() и
и ![]() приводят к тождеству
приводят к тождеству ![]() , а при
, а при ![]() замены
замены ![]() и
и ![]() приводят к точно такому же тождеству. Таким образом, все
свелось к уже разобранному первому случаю. Если теперь обозначить через
приводят к точно такому же тождеству. Таким образом, все
свелось к уже разобранному первому случаю. Если теперь обозначить через ![]() множество всех тех
непрерывных на
множество всех тех
непрерывных на ![]() функций , что
удовлетворяет тождеству
функций , что
удовлетворяет тождеству ![]() , то общее решение можно описать формулой
, то общее решение можно описать формулой
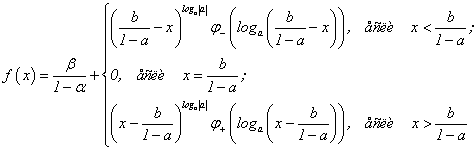
где ![]() , если
, если ![]() , и
, и ![]() , если
, если ![]() . Функции из
. Функции из ![]() легко выражаются через функции из
легко выражаются через функции из ![]() .
.
Если наконец, ![]() и
и ![]() есть некоторое решение уравнения (4), то обозначив через
есть некоторое решение уравнения (4), то обозначив через ![]() сужение
сужение ![]() на
на ![]() , получим
, получим
![]() , если
, если ![]() и
и ![]() , если
, если ![]() .
.
И наоборот, если некоторая непрерывная функция ![]() удовлетворяет
тождеству
удовлетворяет
тождеству![]() , а непрерывная на
, а непрерывная на ![]() функция
функция ![]() определена посредством тождества
определена посредством тождества
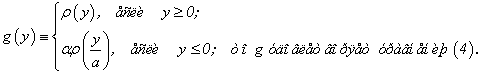
В самом деле, если ![]() , то
, то ![]() и
и ![]() ; а если
; а если ![]() , то
, то ![]() и
и ![]() . Таким образом это последний случай
. Таким образом это последний случай ![]() сводится к предыдущему.
сводится к предыдущему.
Отметим в заключении,
что картина резко изменится, если искать решения уравнения (1) только
среди гладких функций. Картина также
существенно изменится если искать
решения уравнения (1) среди непрерывных функций определенных на некотором открытом луче.
Библиографический список
1. Зорич В.А.
Математический анализ (ч.1, ч.2) . М.: Наука, 1984. – 586 с.
2. Макаров Б.М., Голузина
М.Г., Лодкин А.А. Избранные задачи по вещественному анализу. М.: Наука, 1972. –
193 с.