Dr. Sci. Tech. Smetankina
N.V., Cand. Tech. Sci. Smetankin V.A.,
Smetankin A.V.
The A.N. Podgorny
Institute for Mechanical Engineering Problems of the National Academy of
Sciences of Ukraine, Ukraine
Research of
acoustic fields of hydrodynamic radiators taking into account attenuation of
sound waves
The ultrasonic technics is
widely applied to clearing of details and fluids [1]. However, specific
conditions of technological process of clearing of wool limit ultrasound
application. Complexity of removal of pollution and high requirements to
quality of wool fibers after technological operations leads to that washing is
one most labour-consuming operations [2].
The present work deals
with the process of vibrations of hydrodynamic radiators taking into account
attenuation of sound waves. Sound attenuation is decrease of amplitude and sound-wave
intensity in process of its extending. An attenuation principal cause is
decrease of wave amplitude depending on distance from a source, caused by the shape
and the wave sizes of a source that is a wave divergence.
The radiator consists of a
conic-cylindrical nozzle, a reflector and resonant oscillatory system in the
form of the rods located along the forming cylinder. The converter cylinder has
16 rods in width of 6 mm through 22.5 degrees. The ends of rods are rigidly fixed.
The length of the cylinder is equal 126 mm, and its diameter of 37 mm. The
stream from a nozzle energizes a bending vibration in the rod. The outflow speed
of fluid is 
km/s, the
pressure is 0.61 MPa. Radiators are established in the cylindrical tank
filled with a liquid with surface-active substances. Its density is equal 1010
kg/m3, sound speed is 
km/s, kinematical viscosity 
m2/s. Intensity of
one radiator is 
Âò/ñì2.
For effective operation of
a radiator it is necessary to select such geometrical and mechanical parameters
that its frequency was close to frequency of the first tone of the radiator rod.
Let's construct
mathematical model of studied process. The equation of transverse vibrations of
the rod under the impulse force 
suddenly affixed in point 
is of the form
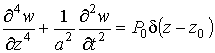, (1)
where 
is Dirac
delta-function in
the point 
;
,
is Young's modulus for
the material of the rod, 
is density for the material
of the rod, 
and 
is width and height of
cross-section of the rod.
The solution of the
equation (1) has the form
,
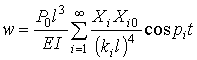where 
is length of the radiator
rod; 
are fundamental circular
frequencies of vibrations; 
are normal functions of the
problem,
;
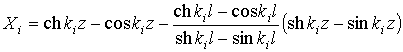is value of normal function
in the point 
. It was accepted that 
.
Fundamental frequencies of radiator
vibrations 
are defined as
.
The frequency of the first
tone calculated under this formula is equal 1750 Hz. In technical calculations fundamental
frequency of radiator rods is defined by the formula [3]
,
where 
. It is 1767 Hz. Thus, for effective operation of radiators it
is necessary to select such parameters that radiator frequency was close to
frequency of the first tone.
The general equations of
dynamics of a fluid and gas turn out from three main principles: conservation
relations of masses; the law on equality between an impulse of forces and a
corresponding increment of quantity of movement; the law of conservation of
energy.
Theoretical and
experimental researches show [3] that radiators at their immersing in a fluid on
depth of 0.2-0.3 m can be observed as spherical sources of the zero order, and
the estimation of efficiency of their operation in the closed areas can be made
on magnitude of a sound pressure. In this case expressions for sound pressure 
and speeds of movement of
environment 
, 
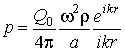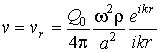, (2)
where 
is productivity of a sound source,
is a sound speed; 
, 
is circular frequency
of vibrations; 
, 
are cylindrical coordinates.
Intensity of a sound field
of a dot source is calculated by the formula
.
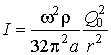Characteristics of a sound
field were defined from Euler's nonlinear equations in the form of Navier-Stokes
jointly with the equation of a condition
, (3)
, (4)
, (5)
where 
is density of the liquid
environment.
The solution of system of
the nonlinear differential equations was carried out by an iteration method.
As the first iteration it
was supposed, that the radiator is replaced with equivalent system of the dot
sources (2). The solution of the homogeneous equations (3), (4) is the generalized
potential of a simple layer. On the found values of speeds from the equations
(4) the density and pressure of a fluid is defined. The following stage
consists in calculation of the right part of the equations (3), construction of
the common solution of system (3)–(5) and refinement of values of density and
pressure of a fluid. Process is completed at reaching of demanded exactitude of
the solution. The system (3)–(5) also considers attenuation of vibrations of
the sound field connected with viscosity of environment.
The account of a sound
attenuation with absorption factor is computed by the formula [4]
,
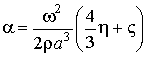where 
and 
are factors of shift
and volume viscosity, accordingly.
Analysis of numerical solution
of ultrasonic field parameters at 
shows that results changes insignificantly.
Thus, the technique of
theoretical research of hydrodynamic radiating system operation is offered. It is established that for the given structural system
parameters the consideration of attenuation of acoustic waves does not lead to
appreciable change of results.
References:
1. Suharkov O.V. Research of
process emulsification in a multifrequency acoustic field // Acoustic Bulletin.
– 2009. – Vol. 12, N 4. – P. 57–64.
2. Scherbak Ya.V. Application
of hydrodynamic radiators for an intensification of processes of washing of
fibrous materials // Bulletin of National Technical University "KhPI".
– 2011.– N 4. – P. 137–140.
3. Physical fundamentals of
ultrasonic technology / edited by L.D. Rosenberg. – Moscow: Nauka, 1970.– 688 p.
4. Ultrasound. Small
encyclopedia. – Moscow: Soviet Encyclopedia, 1979. –400 p.