Математика/ 5. Математическое моделирование

К.ф.-м.н. Рябцева Н.Н., к.ф.-м.н. Харченко А.С.

Белгородский университет кооперации, экономики и права, Россия

О некоторых вариационных неравенствах

на геометрических графах

Уже при постановке вариационных задач для функционалов, заданных на функциях с ветвящимся аргументом, т.е. с аргументом из некоторого геометрического графа (в других терминах – пространственной сети или одномерного клеточного комплекса) возникают некоторые проблемы, связанные с трактовкой интеграла на подобном множестве. Если Г – геометрический граф и – набор всех ребер, то при использовании интеграла по Г возникает вопрос о том, как его трактовать. Первый, самый простой взгляд – как сумму интегралов по ребрам. Однако это – лишь при наглядно наивном определении интеграла, когда он (интеграл) не зависит от того, включаем ли мы концы интервала или нет. Однако уже в стандартной теории функциональных пространств на отрезке, где фундаментальную роль играет функция ограниченной вариации, которая может иметь на концах скачки, а определяемые ими меры–атомы, значение интеграла зависит от принадлежности каждого из концов промежутку, по которому происходит интегрирование. Отмеченное обстоятельство оказывается фундаментальным при описании модели физических систем, у которых ребра–континуумы в общих вершинах–узлах оказываются взаимодействующими, что препятствует присоединению этой вершины только к одному из ребер, когда из остальных ребер она как бы изымается. Некоторым аспектом описанной проблемы мы посвящаем данную работу.

Рассмотрим функционал, определяемый записью

, (1)

где мы сохраняем классическую форму, подразумевая в (1) в качестве и=и(х) скалярнозначные функции, заданные на Г, т.е. и: Г→R. Мы рассматриваем здесь только непрерывные функции, заданные на Г, предполагая их равномерно непрерывными на Г и обозначая их множество через . Для удобства мы предполагаем также, что каждая из рассматриваемых функций дифференцируема на каждом ребре γ_i так, что ее сужение и_i на γ_i оказывается элементом пространства . Для определенности процедуры дифференцирования нам необходимо задание ориентации на каждом ребре, т.е. выбора одного из двух возможных направлений единым образом сразу на всем ребре (тем самым граф должен быть ориентированным). Функцию F трех аргументов, определяющую подынтегральное выражение в (1), мы считаем заданной по первому аргументу – на Г, по второму и третьему – на R, т.е. . Там, где это потребуется мы функцию F будем считать регулярной, т.е. достаточно гладкой – обсуждаемые проблемы определяются другими обстоятельствами, а не трудностями, связанными с потерей гладкости. Описанные договоренности позволяют считать подынтегральное выражение в (1) заданным и непрерывным на каждом ребре если фиксирована функция и(х). Из физических соображений естественно предполагать интеграл аддитивной функцией множества и потому мы подразумеваем развернутую запись для (1) в следующем виде:

(2)

Вторая сумма берется по всем вершинам графа Г, в которых допускается наличие атомов меры. В реальных задачах отмеченные внеинтегральные члены уже для случая отрезка соответствуют классической задаче Больца, а для более общего графа соответствуют наличию в узлах локализованных воздействий, стоков, сосредоточенных масс и прочее.

Если и₀(х) – точка экстремума данного функционала, то реализация классической схемы Лагранжа в виде минимизации функции при произвольном допустимом h приводит к первой вариации:

,

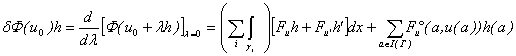причем должно быть для любой допустимой h. Отсюда стандартным образом следуют в силу произвола h(x) аналоги обычных уравнений Эйлера и условие типа

,

которые в приложениях реализуются в виде так называемых условий трансмиссии, т.е. условий стыковки решений, подходящих к узлу а вдоль разных ребер.

Вторая вариация функционала (1) состоит из хорошо известных для задач на отрезке компонент и имеет вид:

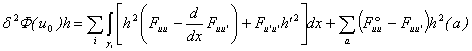(3)

где последняя группа слагаемых суммируется по внутренним узлам.

Переобозначая, как это обычно делается, , , мы можем придать второй вариации канонический вид квадратичного функционала:

.

Нас интересует далее главная часть, т.е. функционал

. (4)

Классическое условие

,

вытекающие из неотрицательности I(h), связываемое обычно с именем Лежандра, возникает в нашей задаче достаточно естественным образом – мы на соответствующих весьма громоздких выкладках не останавливаемся. Нас интересует условие, обеспечивающее строгую положительность (4), и связанные с этим достаточные условия экстремума функционала (1).

Нам далее потребуется функция z(x), обладающая свойством:

. (5)

В классической теории вариационных задач на отрезке подобное равенство гарантировано для любой гладкой z(x), поскольку если Г=[a, в], то

,

т.к. h(a)=h(в)=0 в силу условия закрепления концов. В нашей ситуации прямое использование формулы Ньютона–Лейбница невозможно, и поэтому вопрос о выполнении равенства (5) мы откладываем пока в сторону, предполагая, что используемые далее z(х) этому равенству удовлетворяют.

Для любой такой функции на каждом ребре мы можем преобразовать левую часть (5) к виду:

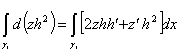
и добавить к каждому (по ) интегралу в (4), что приведет нас к выражению:

. (6)

Если окажется, что для z(x) выполняется равенство:

, (7)

то для такой функции z(х) представление функционала (6) приобретет вид:

,

откуда мгновенно будет следовать, что для любого допустимого h.

Таким образом, вопрос о неотрицательности второй вариации исходного функционала или, что тоже самое, о неотрицательности функционала (4), сведен к вопросу о существовании функции z(x), удовлетворяющей равенствам (5) и (7).

Введем в рассмотрение уравнение

(8)

интерпретируя его обычным образом на каждом ребре графа Г. Пусть - такое его решение, которое непрерывно во всех внутренних вершинах Г, а в каждой из них удовлетворяет дополнительному условию

(9)

где суммирование производится по всем ребрам, примыкающим к а, а - крайняя производная в точке х=а сужения на ребро (примыкающее к а).

Каждое из уравнений (8) на своем ребре адекватно классическому уравнению Якоби.

Скажем, что для нашей задачи выполняется Г–условие Якоби, если существует непрерывное на Г решение уравнения (8), удовлетворяющее (9) и равномерно положительное в целом на Г.

Теорема. Если inf P>0 выполняется Г–условие Якоби, то квадратичный функционал (4) наверняка неотрицателен.

Доказательство основано на двух обстоятельствах. Если - строго положительное на Г решение уравнения (8), то вводимая заменой

(10)

функция удовлетворяет на каждом уравнениям (7), обеспечивая тем самым возможность записи I(h) на каждом ребре в виде . При этом условия (9) гарантируют по функции (10) справедливость (5) для всех допустимых h. На деталях достаточно объемных выкладок мы здесь не останавливаемся.

Литература.

1. Покорный Ю.В., Пенкин О.М., Прядиев В.Л., Боровских А.В., Лазарев К.П., Шабров С.А. Дифференциальные уравнения на геометрических графах. – ФИЗМАТЛИТ, Москва, 2003.

2. Об интегрировании в вариационных неравенствах на пространственных сетях / Ю.В. Покорный, И.Ю. Покорная, В.Л. Прядиев, Н.Н. Рябцева // Математические заметки. – 2007. – 81:6. – С. 904-911.

3. Покорный, Ю.В. О вариационных уравнениях на пространственных сетях / Ю.В. Покорный, Н.Н. Рябцева // Научные ведомости БелГУ. Математика. Физика. – 2011. – № 5 (100). – С. 88-98.