А.И. Долгарев

МНОГОМЕРНЫЕ ПОВЕРХНОСТИ I.

ВЫРАЖЕНИЕ КОЭФФИЦИЕНТОВ ВТОРОЙ КВАДРАТИЧНОЙ ФОРМЫ

ЕВКЛИДОВОЙ ПОВЕРХНОСТИ

ЧЕРЕЗ КОЭФФИЦИЕНТЫ ПЕРВОЙ КВАДРАТИЧНОЙ ФОРМЫ

Известна теорема Бонне (1867 год) об определяемости поверхности 3-мерного евклидова пространства коэффициентами ее основных первой и второй квадратичных форм. Условиями определяемости являются формулы Гаусса – Петерсона – Кодацци. К настоящему времени изучены основные случаи определяемости поверхностей размерности в евклидовом мерном пространстве , , [1]. Установлено, что поверхность пространства определяется своей первой квадратичной формой, но в доказательстве этого факта используются и вторая квадратичная форма поверхности и формулы Гаусса – Петерсона – Кодацци. Свойства поверхностей евклидова пространства изложены в [2, разделы 3, 4], где выделены поверхности пространства . Вместе с тем имеются работы [3, 4, 5], в которых для поверхностей пространства коэффициенты второй квадратичной формы выражены через коэффициенты ее первой квадратичной формы. При этом уравнения Гаусса – Петерсона – Кодацци не используются. В [6] и [4, 5] показано, как получается евклидова поверхность по коэффициентам первой квадратичной формы в результате решения системы линейных уравнений с частными производными.

Ниже коэффициенты второй квадратичной формы поверхности многомерного евклидова пространства , , выражены через коэффициенты первой квадратичной формы. Используются основные понятия из [1] и [2]. В символике и терминологии иногда имеются понятные отступления от [1, 2]. Определяемость поверхности пространства ее метрической квадратичной формой установлена на основе выражения коэффициентов формы кривизны через коэффициенты метрической формы.

1. Евклидово пространство

Через принято обозначать многообразие кортежей длины действительных чисел, . Кортежи понимаются в двух качествах. (а) Кортежи называются точками, обозначаются ; используется запись = . Элементы кортежей (числа) называются координатами точки. При рассмотрении кортежей функций имеются изменяющиеся кортежи, их элементы могут называться компонентами. (б) Кортежи называются векторами при условии, что над ними заданы: операция сложения и операция умножения кортежей на действительные числа, связанная со сложением кортежей; требуется, чтобы алгебраическая структура являлась линейным пространством над полем . Векторы обозначаются: , . Указанное линейное пространство обозначается . Если на определено евклидово скалярное произведение векторов (оно обозначается , или , или другим символом), то имеется евклидово векторное пространство . (в) Рассматривается отображение , в котором всякой паре точек соответствует единственный вектор и выполняются аксиомы Г. Вейля аффинного пространства. Многообразие с евклидовым векторным пространством называется евклидовым пространством и обозначается .

2. Поверхности евклидова пространства,

В обзоре [1] по теории поверхностей мерного евклидова пространства рассматриваются мерные поверхности как погружения класса , , . Поверхность есть образ в паре с погружением мерного многообразия , , в . Погружение и поверхность записывается в виде

. (1)

Это поверхность-график, или явно заданная поверхность. В [2] в случае поверхность записывается векторной функцией

.

Если , то, разумеется, поверхность описывается векторной функцией

, (2)

компоненты , не зависят от . В [1,2] поверхности описываются функциями (1) . При многообразие (1) мерно (см. [2]). Как многообразие, может быть описано одним уравнением или системой уравнений, [2, с. 180 – 183]. При в [1] поверхность описывается одним уравнением. Рассмотрим этот факт поподробнее.

Пусть , . Поверхность описывается явной функцией и векторной функцией , компонента от не зависит. Точка = = лежит на поверхности только в случае, если координаты точки удовлетворяют уравнению поверхности . Координата при этом произвольна, координаты точек = удовлетворяют уравнению , т.е. прямая , определяемая точкой и вектором лежит на поверхности (рассуждения из курса аналитической геометрии). Поверхность является цилиндрической, ее образующие параллельны координатной оси . Направляющая поверхности лежит в координатной плоскости пространства .

1. ЛЕММА. Поверхность есть прямая сумма = плоской линии и прямой , не лежащей в плоскости линии . #

В общем случае в мерном пространстве поверхность , , описывается функцией (2). Пусть точка поверхности , ее координаты удовлетворяют уравнению . Точка такова, что ее координаты удовлетворяют уравнению . Пусть вектор, ая координата которого равна 1 и все другие координаты равны 0. Поэтому всякая прямая лежит на поверхности . Тем самым, установлена

2. ЛЕММА. Поверхность (2), , пространства является цилиндрической, содержащей плоскость , размерность этой плоскости равна . #

Возможно рассматривать пространство как прямую сумму пространств = +. Поверхность является гиперповерхностью подпространства , в котором она описывается функцией . По лемме 1, выполняется

3. ЛЕММА. Цилиндрическая поверхность пространства , , является прямой суммой гиперповерхности подпространства и плоскости пространства : =. #

В связи с обнаруженными свойствами, о поверхностях лучше говорить как о подмногообразиях параметров многообразия . Поверхность размерности пространства , , можно задать несколькими функциями, например,

, , .

Неисследованными остаются поверхности следующего вида

.

3. Касательная плоскость поверхности

Производные функции векторной функции , согласно (2), есть

, . (3)

, в противном случае от не зависит. Поверхность регулярна класса , существуют производные до го порядка включительно и векторы , , линейно независимы. Всякий вектор имеет две ненулевые компоненты: ую и ую, остальные компоненты векторов равны нулю. Имеется касательных векторов поверхности . Согласно лемме 2, векторы прямых , лежащих на поверхности , являются касательными векторами поверхности вдоль этих прямых.

4. ЛЕММА. Касательная плоскость поверхности в каждой ее обыкновенной точке является мерной, порождается касательными векторами и векторами прямых , лежащих на поверхности:

= . (4)

# Все указанные векторы касаются координатных линий на поверхности или являются векторами прямых на поверхности, векторы линейно независимы. #

4. Нормальная плоскость поверхности

Вектор из , перпендикулярный всем векторам касательной к поверхности плоскости , является нормальным вектором поверхности. В [1] считается, что поверхность имеет нормальных векторов в каждой своей обыкновенной точке и эти векторы порождают мерную нормальную плоскость поверхности . Однако, лемма 2 говорит о другом.

5. ЛЕММА. Нормальная плоскость поверхности (2) во всякой ее обыкновенной точке является 1-мерной, т.е. является нормалью поверхности.

# Векторное пространства евклидова пространства , содержащего поверхность , является мерным. Размерность касательного пространства поверхности равна , лемма 4. Следовательно, размерность нормальной плоскости равна 1 и эта плоскость является прямой линией. #

Для дальнейшего изучения поверхностей пространства важно указать координаты вектора нормали поверхности в точке .

Пусть = , = – векторы, ненулевыми компонентами которых являются только компоненты с номерами ; где . Рассматриваем бивекторы = ,

=

с теми же ненулевыми компонентами. Выполняется

6. СВОЙСТВО. Бивектор ортогонален векторам и . #

О бивекторах см., например, [7, с. 56 – 74]. В частности, имеем для касательных векторов

7. СВОЙСТВО. Для векторов получается

. (5)

# Пусть = , = . В этом случае , , , . В (5) выписаны только ненулевые компоненты вектора . #

Перечислим свойства векторов , , .

8. СВОЙСТВО. Модули всех векторов больше 1 и

, , . # (6)

9. СВОЙСТВО. Скалярные произведения векторов , , равны:

, , , . (7)

Выполняется

. # (8)

10. СВОЙСТВО. при и . #

По виду (5) вектора запишем поливектор

, (9)

последние компонент которого равны 0 , его скалярный квадрат равен

, (10)

модуль есть

.

Точнее, поливектор есть вектор (о р-векторах, , см. [8, с. 275 – 281].

11. СВОЙСТВО. Вектор (9) является ортогональным к векторам касательных линий поверхности и векторам прямых , лежащих на поверхности . Вектор

(11)

является единичным вектором нормали поверхности в точке .

# Действительно, , и . #

12. ТЕОРЕМА. Вектор = пространства ортогонален касательной плоскости только если он коллинеарен вектору (11).

# Пусть вектор ортогонален плоскости . Тогда выполняются равенства: для всех , т.е. . Понятно, что . Для всех справедливо: и вектор коллинеарен , = . Значения координат определяются из равенств : если , то . #

5. Фундаментальные формы поверхности

В координатах на поверхности имеем кривую на поверхности

,

вектор касательной к линии = есть (как вектор полной производной по ):

=, (12)

скалярный квадрат вектора равен

=. (13)

Метрической формой поверхности (первой основной квадратичной формой, первой фундаментальной квадратичной формой) называется

= , , (14)

коэффициенты метрической формы есть скалярные произведения векторов касательных линий на поверхности . Значения коэффициентов формы таковы:

и . (15)

Нормальной кривизной линий на поверхности относительно нормали является

.

Согласно (12), =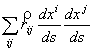+, и по (11), нормальная кривизна линий на поверхности равна

. (16)

Значения скалярных произведений таковы: =. Обозначим

. (17)

Теперь кривизна линий на поверхности относительно нормали (11) такова

. (18)

Формой кривизны поверхности (второй основной квадратичной формой, второй фундаментальной квадратичной формой) относительно нормали называется

, (19)

ее коэффициенты есть (17). Формула (18), с учетом (19) и (13), принимает вид

,

нормальная кривизна линий на поверхности равна отношению формы кривизны к метрической форме поверхности. Можно говорить о нормальной кривизне линий на поверхности , а не о кривизне линий на поверхности относительно нормали , так как нормаль поверхности единственна, лемма 5.

6. Выражение коэффициентов формы кривизны поверхности

через коэффициенты метрической формы

Для коэффициентов форм и евклидовой поверхности размерности выполняется утверждение, аналогичное утверждению для поверхностей 3-мерного евклидова пространства, см. [3].

13. ТЕОРЕМА. Коэффициенты формы кривизны поверхности выражаются через коэффициенты метрической формы поверхности и их производные первого порядка. Формулы зависимости таковы:

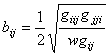, , . (20)

# По первой из формул (15),

.

Производные величин равны

. (21)

По (17) при , , это первая формула в (20). По (21), (17) находим

, .

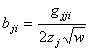Т.к. , то, с использованием второй формулы в (15), находим

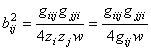, (22)

откуда получается вторая формула в (20). #

На основании (10) и первой из (15) имеем

. (23)

14. ЛЕММА. Выполняется соотношение 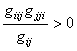. Выражения и имеют один и тот же знак.

# Утверждение является следствием формулы (22). #

Таким образом, подкоренные выражения в формулах (20) положительны. Справедлива следующая

15. ТЕОРЕМА. Форма кривизны (вторая основная квадратичная форма) мерной поверхности мерного евклидова пространства имеет вид

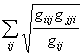=(+). (24)

Здесь коэффициенты метрической формы поверхности.

# Подставляем в (19) формулы из (20). #

Метрическая форма (13) поверхности и форма кривизны (24) поверхности записаны через коэффициенты в (14) метрической формы поверхности .

7. Определяемость поверхности мерного пространства

Установлено, см. [1, теоремы 9.1, 9.6, 9.7, 9.10], что поверхность евклидова пространства , , определяется однозначно, с точностью до положения в пространстве , своими формами: метрической и кривизны, при выполнении вполне определенных условий на коэффициенты указанных квадратичных форм в виде формул Гаусса – Петерсона – Кодацци. Это содержание основной теоремы теории поверхностей. На основании доказанной выше теоремы 13, основная теорема теории поверхностей существенно упрощается.

16. ТЕОРЕМА. (основная теорема теории поверхностей) Поверхность евклидова пространства , , однозначно, с точностью до положения в пространстве, определяется своей метрической формой.

# Утверждение является следствием приведенных в [1] теорем об определяемости поверхности и теоремы 13. #

В доказательстве теоремы 13 не налагается никаких условий на коэффициенты форм и ; в частности, теорема 13 верна и при условиях из теорем, приведенных в [1].

8. Выделение гиперповерхностей

При имеем гиперповерхность

.

Для неё выполняются известные свойства. Поверхность имеет касательную плоскость и единственную нормаль =, , = =, см. (3) и (9). Метрическая форма и форма кривизны имеют один и тот же вид независимо от соотношения между числами и . Нормаль поверхности единственна. Формулы (20) и (24) остаются неизменными.

Случай . Коэффициенты метрической формы и формы кривизны выписаны выше с точностью до обозначений. Имеем:

;. , , , .

В [3] получены выражения коэффициентов формы кривизны через коэффициенты метрической формы:

, , .

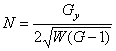Это запись формул (20) в другой символике. Поверхность определяется своей метрической формой. Факт не зависит от формул Гаусса – Петерсона – Кодацци.

Если , то является цилиндрической поверхностью размерности в мерном пространстве. Многообразие может быть описано одним уравнением или несколькими уравнениями, [2, пп. 12.6 и 12.7, с. 180 – 183]. В первом случае имеется гиперповерхность, во втором – цилиндрическая поверхность, в подпространстве она является гиперповерхностью, лемма 3.

Список литературы

1. I. Ivanova-Karatopraklieva, P.E. Markov, I. Kh. Sabitov. Bending of surfaces. III. Fundamentalnaya i prikladnaya matematika, vol 12. (2006), no 1, pp. 3 – 56.
2. Иванов А.О., Тужилин А.А. Лекции по классической дифференциальной геометрии. – М.: Новая университетская библиотека, 2009 – 233с.
3. Долгарев А.И. Новый вид основной теоремы Гаусса в евклидовой теории поверхностей. //Materiali IX mezinarodni vedecko-praktika conference «Dni vedy – 2013» - Dil 32. Matematika. Vystavba a archtektura: Praga. Publiching House “Education and Skience”. s.r.o. – 2013. С. 55 – 60.
4. Долгарев И.А. и Долгарев А.И. Определяемость евклидовой поверхности. Обнов-

ленная основная теорема теории поверхностей (обзор теории поверхностей).// Mate-

rialy IX Miedzynarodowej naukowi-praktycznej konferencji “Perspektywiczne opra-

cowania sa nauka I technikani – 2013” Volume 33. Matematyka.: Przemysl. Nauka i

studia – 2013, C. 27 – 47.

5. Долгарев И.А., Долгарев А.И. Обновленная основная теорема теории поверхностей в курсе геометрии. // Информационные технологии в математике и математическом образовании. Материалы II Всероссийской научно-методической конференции. Красноярск: КГПУ – 2013, С. 327 – 331.
6. Долгарев А.И. Система линейных уравнений первого порядка в частных производ-

ных. Задание евклидовой поверхности коэффициентами ее первой квадратичной

формы. // Materiali IX mezinarodni vedecko-praktika conference «Dni vedy – 2013» -

Dil 32. Matematika. Vystavba a architektura: Praga. Publiching House “Education and

Skience”. s.r.o. – 2013. С. 32 – 40.

7. Постников М.М. Лекции по геометрии. Семестр 1. Аналитическая геометрия. М.:

Наука, 1979. – 336 с.

8. Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия. – 2-ое изд. – М.: Нау-

ка, 1986. – 304 с.