Кравець В.С.

науковий керівник: к.ф.-м.н., доцент Дрінь Я.М.,

Буковинський державний фінансово-економічний університет,

м. Чернівці

Одним із важливих явищ в економіці держави є випуск продукції, оскільки він характеризує кількість експорту товарів, визначає прибуток підприємств. Випуск продукції є одним із складових національних рахунків, який в свою чергу впливає на макроекономічні показники. Але щоб збільшити цей показник потрібно багато ресурсів, серед яких і можуть бути фінансові активи та зобов’язання. Тож на основі таких показників побудуємо економетричну модель залежності випуску продукції від фінансових активів та зобов’язань.

Для дослідження були використані статистичні дані за 2001-2011 роки. У таблиці 1 наведено дані про випуск продукції та фінансові зобов’язання та активи [3,4].

Таблиця 1. Співвідношення випуску продукції до фінансових активів та зобов’язань за 2001-2011 роки

( млн. грн.)

Роки	Випуск продукції	Фінансові зобов’язання	Фінансові активи
2001	460520	5380	14583
2002	504008	5967	15649
2003	603704	6510	16792
2004	809988	43129	79804
2005	995630	81584	93781
2006	1182179	94336	87146
2007	1565055	196471	164445
2008	2072172	189927	127144
2009	1955685	47740	41831
2010	2388289	169964	158145
2011	2895283	134174	61090

Щоб з’ясувати, чи існує зв’язок між цими чинниками, використано множинну лінійну регресію. Дослідження економетричної моделі скалається з таких етапів:

І. Специфікація моделі. Виберемо за незалежні змінні Х₁ – фінансові активи, Х₂ – фінансові зобов’язання, за залежну змінну Y – випуск продукції. Розрахунки проведені за допомогою програми MS Exel, показали, що залежності між Х₁, Х₂ та Y можна подати лінійною множинною моделлю з високим ступенем узгодженості R².

ІІ. Обчислення статистичної оцінки для вектора та побудова моделі. Оцінки параметрів лінійної економетричної моделі здійснювались за методом найменших квадратів з якого випливає формула оцінки параметрів лінійної регресії:

,

де - транспонована матриця до матриці[2].

Тож матриця на буде такого вигляду:

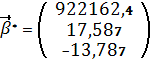
Отже, виходячи з [2], знайдені такі оцінки вектора { β₀, β₁, β₂}:

β₀ = 922162,4, β₁ = 17,587, та β₂ = -13,787.

На основі цих даних побудуємо модель використовуючи формулу:

; ,

ІІІ. Аналіз ступеня адекватності побудованої моделі та вибіркових даних. Обчислимо вектор за формулою . Результати розрахунків наведені в таблиці 2. Правильність виконаних розрахунків можна перевірити, порівнюючи значення та , де

,

оскільки , попередні розрахунки правильні.

Визначимо ступінь адекватності моделі за статистичними даними, порівнюючи відхилення між фактичними значеннями та результатами обчислень за моделлю. Запишемо їх як елементи вектора [2].

Середнє значення , отже, розбіжностей не існує, а це означає що модель адекватна.

IV. Перевірка статистичної значущості коефіцієнта детермінації R² та критерію Фішера. Коефіцієнт детермінації R² = 0,6977 показує, що на 69,77 % варіація випуску продукції пояснюється фінансовими активами та зобов’язаннями .

Також дуже високий коефіцієнт кореляції вказує на тісну близьку до функціональної, залежність незалежних змінних Х₁ та Х₂ з залежною змінною Y.

Статистичну значущість моделі перевіряємо за допомогою F-критерію. Фактичне значення критерію порівнюємо з табличним значенням при ступенях вільності k₁ = 2, k₂ = 8 і рівні значущості α = 0,05 . Оскільки гіпотеза про істотність зв’язку між залежною і незалежними змінними в даній економетричній моделі підтверджується, тобто лінійна форма зв’язку в моделі вибрана правильно.

V. Визначення дисперсій оцінок та їх стандартних помилок. Знайдемо тепер незміщену оцінку для дисперсії залишків за формулою:

де n = 11, m = 2.

Отже, незміщена оцінка для дисперсії залишків = 25997000000. Далі ми знаходимо коваріаційну матрицю оцінок параметрів для виявлення дисперсій, яка визначається за формулою:

.

Визначивши матрицю ми знаходимо дисперсії оцінок параметрів, де вони дорівнюють добуткам діагональних елементів c_ij матриці [2].

Середньоквадратичні відхилення оцінок параметрів вийшли:

280139,25; 5,231; 7,09.

Перевіримо статистичну значущість параметрів β₀, β₁ та β_2. Для цього ми скористаємось критерієм Стьюдента, де спостережувані значення статистичних критеріїв дорівнюють:

.

Для побудови двобічної критичної області при α = 0,05, k = n – m – 1 = =11 – 2 – 1 = 8 знаходимо (α/2, k) = (0,025;13) = 2,306. Оскільки , , то відкидаємо гіпотезу про присутність мультиколінеарності.

VI. Розрахунок довірчих інтервалів для оцінок параметрів β₀, β₁ та β₂. Довірчі інтервали оцінок параметрів такі:

276161,319 < < 1568163,54 ;

5,524 < < 29,651;

-30,135< < 2,562 .

На основі побудованої регресії можна зробити висновок, що випуск продукції, яке залежить від кінцевих споживчих витрат, рівних середнім значенням = 88652,909 млн. грн. та = 78219,091 млн. грн., дорівнювала би при β₀ = – середньому значенню залежної змінної = 1402955,73 млн. грн. Збільшення фінансових зобов’язань та зменшення фінансових активів, які були використані для збільшення результативного показника за один рік призводить до збільшення випуску продукції. Фактори, включені в модель пояснюють «поведінку» випуску продукції на 69,77%.

VII. Розрахунок прогнозного значення та побудова для нього довірчих інтервалів. Оскільки значення проміжного споживання залежить від споживчих витрат, доцільно розрахувати точковий прогноз та довірчі інтервали прогнозу. Для цього задамо вектор прогнозних значень незалежних змінних x_p =138199,22 млн. грн. – фінансові зобов’язання та 63289,24 млн. грн. – фінансові активи [1]. Ці дані ми взяли на 2014 рік. Тож, прогнозне значення ВВП дорівнює

;

тобто прогнозне проміжне споживання на 2014 рік становить 2480176,09 млн. грн.

Далі ми знаходимо можливе відхилення s_p :

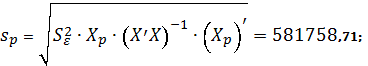
де – матриця прогнозних значень, - транспонована матриця до матриці . Отже, похибка проміжного споживання дорівнює 581758,71 млн. грн.

Обчислюємо нижню та верхню межу прогнозного значення :

1138640,5 < < 3821711,68

Отже, потенційне проміжне споживання на 2014 рік може коливатися приблизно від 1138640,5 млн. грн. до 3821771,68 млн. грн.

Також спробуємо використати нелінійну модель, щоб визначити,яку доцільніше використовувати для визначення прогнозних показників. Зробивши розрахунки за допомогою функції Кобба-Дугласа ми побудували таку модель:

; .

Коефіцієнт детермінації R² становить 0,9076, а в лінійній множинній регресії він становить 0,6799. Отже краща варіація підтверджується у регресії Кобба-Дугласа. Далі ми розрахували прогнозне значення ВВП за допомогою нелінійної функції, який становить 2970979 млн. грн. порівняно з 2480176,09 млн. грн. в лінійній функції. Отже, як ми бачимо, що і лінійна, і нелінійна функція є коректною, тому що, при розрахунку прогнозного значення, де ми бачимо незначні відхилення від прогнозного значення лінійної функції, які дають нам реалістичні прогнозні дані на 2014 рік випуску продукції з урахуванням як негативних, так і позитивних факторів за допомогою використання довірчих інтервалів. Тож, можна сказати, що при виявленні зв’язку між випуском продукції та фінансовими активами і зобов’язаннями, а також прогнозуванні цього показника доцільно використовувати обидві регресії.

У даній роботі побудовано моделі парної множинної регресії та регресію Кобба-Дугласа, які описують зміни випуску продукції враховуючи зміни фінансових ресурсів. Отже, як і ми передбачали, що на випуск продукції мають немалий вплив фінансові ресурси, що і підтверджує коефіцієнт детермінації. За допомогою отриманих моделей можна робити прогноз щодо випуску продукції на майбутні періоди, а також визначити як може коливатися випуск продукції при негативних та позитивних факторах, використовуючи довірчі інтервали. Також довели, що ефективно використовувати цей метод при визначенні прогнозного показника і при його використанні можна зменшити витрати, які витрачаються на розрахунок вищезазначеного показника.

Список використаної літератури

1. Україна: Перспективи розвитку – консенсус-прогноз: Міністерство економічного розвитку і торгівлі України, 2013. – 35 с.

2. Економетрія: Навч. Посіб. / В.І. Жлуктенко, Н.К. Водзянова, С.С. Савіна, О.В. Колодінська; За загальною редакцією кандидата економічних наук С.І. Наконечного. – К.: Видавництво Європ. ун-ту, 2005. – 552 с.

3. Статистичний щорічник України за 2011 рік. – К.: Техніка,2012. – 558 с.

4. Випуск продукції за 2001-2011 рр.: [Електронний ресурс] : Державний комітет статистики України. — Режим доступу: http://www.ukrstat.gov.ua.