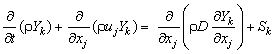К. С. Щербакова,
И. В. Ситников, Н. И. Атапин, А. А. Однолько
Воронежский
государственный архитектурно-строительный университет, Россия
Сравнение
результатов численного моделирования динамики опасных факторов пожара,
полученных на основе интегральной и полевой математических моделей
С принятием
технического регламента «О требованиях пожарной безопасности» [1] в России осуществлен переход к гибкому
объектно-ориентированному противопожарному нормированию, идея которого заключается
в оценке безопасности объекта защиты посредством определения величины пожарного
риска. Основной частью определения величины индивидуального пожарного риска
является сравнение требуемого времени эвакуации с расчетным. Требуемое время
эвакуации рекомендуется рассчитывать с помощью трех типов математических
моделей динамики опасных факторов пожара: интегральной, зонной и полевой
(дифференциальной) [2-4]. Методика определения
величины пожарного риска [5] допускает применять как полевые, так и интегральные
математические модели пожара, однако, результаты их применения значительно
расходятся. Стоит отметить, что нормативными документами не определено, какие
именно результаты следует принимать во внимание. Это может привести к
столкновению интересов обеспечения пожарной безопасности и снижения стоимости
строительства. Рассмотрим данную проблему на примере моделирования динамики
опасных факторов пожара для производственного помещения с помощью интегральной
и полевой моделей.
Интегральные математические
модели пожара в самом общем виде описывают процесс изменения основных
параметров газовой среды помещения во времени, усредняя при этом их значения по
объему. Модели основаны на фундаментальных законах сохранения массы и энергии и
имеют следующий вид (1-7):
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
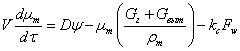 (7)
(7)
где ρm – среднеобъемная
плотность, кг/м3; pm – среднеобъемное
давление, Па; Tm – среднеобъемная температура, К; μm – среднеобъемная
оптическая плотность, Нп/м; ρO2 – среднеобъемная
парциальная плотность кислорода, кг/м3; ρCO – среднеобъемная парциальная
плотность угарного газа, кг/м3; ρCO2 – среднеобъемная парциальная плотность
углекислого газа, кг/м3; ρHCl – среднеобъемная парциальная плотность хлористого
водорода, кг/м3; ![]() – объем помещения, м3;
– объем помещения, м3; ![]() – время развития пожара, с;
– время развития пожара, с; ![]() –
скорость выгорания (скорость газификации) горючего материала, кг/с; Gв – массовый расход поступающего в помещение
воздуха из окружающей атмосферы посредством естественной вентиляции, кг/с; Gг – массовый расход выходящих газов из помещения
в окружающую атмосферу посредством естественной вентиляции, кг/с;
–
скорость выгорания (скорость газификации) горючего материала, кг/с; Gв – массовый расход поступающего в помещение
воздуха из окружающей атмосферы посредством естественной вентиляции, кг/с; Gг – массовый расход выходящих газов из помещения
в окружающую атмосферу посредством естественной вентиляции, кг/с; ![]() – массовый расход, создаваемый механическим
притоком, кг/с; Gвыт – массовый расход, создаваемый механической
вытяжкой, кг/с;
– массовый расход, создаваемый механическим
притоком, кг/с; Gвыт – массовый расход, создаваемый механической
вытяжкой, кг/с; ![]() – показатель адиабаты; η – коэффициент полноты сгорания;
– показатель адиабаты; η – коэффициент полноты сгорания; ![]() – низшая теплота сгорания, Дж/кг; iг – энтальпия газовой среды, Дж/кг;
– низшая теплота сгорания, Дж/кг; iг – энтальпия газовой среды, Дж/кг; ![]() – удельная изобарная теплоемкость газовой
среды, Дж/кг К; Qw – суммарный тепловой поток в ограждения, Вт;
– удельная изобарная теплоемкость газовой
среды, Дж/кг К; Qw – суммарный тепловой поток в ограждения, Вт; ![]() – потребление кислорода, кг/кг; xO2 – массовая доля
кислорода в помещение при пожаре;
– потребление кислорода, кг/кг; xO2 – массовая доля
кислорода в помещение при пожаре; ![]() – стехиометрический коэффициент для угарного
газа, кг/кг; xCO – средняя массовая доля угарного газа в
помещение при пожаре;
– стехиометрический коэффициент для угарного
газа, кг/кг; xCO – средняя массовая доля угарного газа в
помещение при пожаре; ![]() – стехиометрический коэффициент для
углекислого газа, кг/кг; xCO2 –
средняя массовая доля углекислого газа в помещение при пожаре;
– стехиометрический коэффициент для
углекислого газа, кг/кг; xCO2 –
средняя массовая доля углекислого газа в помещение при пожаре; ![]() – стехиометрический коэффициент для
хлороводорода, кг/кг; xHCl – средняя массовая доля
хлористого водорода в помещение при пожаре;
– стехиометрический коэффициент для
хлороводорода, кг/кг; xHCl – средняя массовая доля
хлористого водорода в помещение при пожаре; ![]() – коэффициент седиментации частиц дыма на
поверхностях ограждающих конструкций, Нп/с;
– коэффициент седиментации частиц дыма на
поверхностях ограждающих конструкций, Нп/с; ![]() – площадь поверхности ограждений, м2.
– площадь поверхности ограждений, м2.
Применение интегральных
математических моделей пожара рекомендуется для помещений малого объема простой
геометрической формы для предварительных расчетов [2].
Полевые математические модели пожара позволяют
смоделировать динамику опасных факторов пожара в каждой точке рассматриваемого
объема, используя при этом законы механики сплошных сред. Основой для полевых
моделей пожара являются уравнения, выражающие законы
сохранения массы, импульса, энергии и масс компонентов в рассматриваемом объеме
(8-12):
![]() (8)
(8)
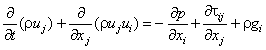 (9)
(9)
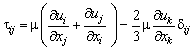 (10)
(10)
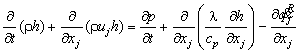 (11)
(11)
где ![]() – статическая
энтальпия смеси;
Нk – теплота
образования k-го компонента;
– статическая
энтальпия смеси;
Нk – теплота
образования k-го компонента;
![]() – теплоемкость смеси при постоянном давлении;
– теплоемкость смеси при постоянном давлении;
![]() – радиационный поток энергии в направлении xj.
– радиационный поток энергии в направлении xj.
Для
замыкания системы уравнений (8-12) используется уравнение состояния идеального
газа, которое имеет вид:
![]() , (13)
, (13)
где Rо –
универсальная газовая постоянная; Mk – молярная
масса k-гo компонента.
На рис. 1 представлено производственное помещение с
обращением горючей жидкости, для которого смоделирована динамика основных
параметров газовой среды [6] с помощью следующих программных продуктов:
-
интегральной
математической модели пожара;
-
аналитического
решения интегральной математической модели пожара;
-
программного
комплекса СИТИС ВИМ [7];
-
программного
комплекса PyroSim [8].
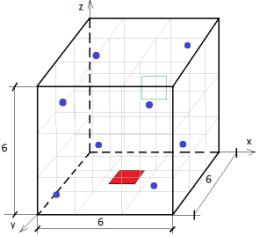
Рис. 1. Производственное помещение с обращением горючих
жидкостей
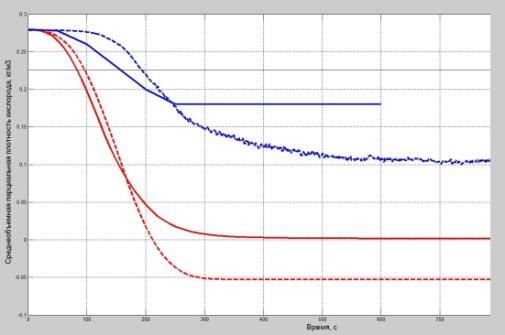
Расхождение результатов, полученных посредством
разных моделей, показано на рис. 2 на примере динамики изменения среднеобъемной
парциальной плотности кислорода газовой среды при пожаре в помещении.
![]()
 – исходная интегральная
математическая модель пожара;
– исходная интегральная
математическая модель пожара;
![]()
 – аналитическое решение
интегральной математической модели пожара;
– аналитическое решение
интегральной математической модели пожара;
![]()
 – СИТИС ВИМ;
– СИТИС ВИМ;
![]()
 – PyroSim;
– PyroSim;
![]()
 – критическое значение
опасного фактора пожара.
– критическое значение
опасного фактора пожара.
Рис. 2. График изменения
среднеобъемной парциальной плотности кислорода в газовой среде при пожаре в
помещении
По полученным графикам прослеживается
расхождение между временем наступления критического значения по каждому из
опасных факторов пожара, рассчитанным по интегральной математической модели, и
временем, рассчитанным по полевой математической модели. Результаты численного
эксперимента сведены в таблицу.
Таблица
Время наступления критического значения
опасных факторов пожара
|
Опасный
фактор пожара |
Время
наступления критического значения опасных факторов пожара, определенное по
следующим программным продуктам, с |
|||
|
Исходная
интегральная математическая модель пожара |
Аналитическая
интегральная математическая модель пожара |
СИТИС
ВИМ
|
PyroSim |
|
|
Среднеобъемная
плотность HCL |
50 |
50 |
100 |
240 |
|
Среднеобъемная
плотность O2 |
80 |
95 |
155 |
197 |
|
Среднемассовая
температура |
80 |
90 |
145 |
190 |
Сравнительный анализ
этих моделей показал, что время наступления критического значения по каждому из
опасных факторов пожара существенно отличаются для выбранного помещения. При
сравнении необходимого времени эвакуации, полученного в ходе расчета по
интегральной и полевой моделям при одинаковых исходных данных получили
расхождение результатов. Это может привести к неточной оценке пожарного риска
объекта строительства. Вместе с тем, нормативными документами не определено,
какие результаты следует принимать во внимание, что провоцирует конфликт
интересов обеспечения пожарной безопасности и снижения стоимости строительства.
Указанные проблемы требует более
глубоких теоретических и экспериментальных исследований.
Литература
1. Федеральный закон N
123 – ФЗ «Технический регламент о требованиях пожарной безопасности». – Введ.
2008 – 07 – 22. – М.: НЦ ЭНАС, 2008. – 64 с.
2. Кошмаров Ю. А.
Прогнозирование опасных факторов пожара в помещении: Учебное пособие. – М.:
Академия ГПС МВД России. – 2000. –118 с.
3. Ситников, И.В. Анализ
математических моделей пожара, применяемых для расчета времени блокирования
путей эвакуации опасными факторами пожара / И.В. Ситников, И.А. Шепелев, С.А.
Колодяжный, А.А. Однолько // Инженерные системы и сооружения: Воронеж. гос.
арх.– строит. ун-т. – №1(6) – 2012. – С. 81 – 87.
4. Однолько, А.А. Проблемы
применения математических моделей, определяющих время блокирования путей
эвакуации опасными факторами пожара при расчете пожарного риска / А.А.
Однолько, И.В. Ситников // Инженерные системы и сооружения: Воронеж. гос. арх.–
строит. ун-т. – №1(2) – 2010. – С. 185 – 191.
5.
Методика определения расчетных величин пожарного
риска в зданиях, сооружениях и строениях различных классов функциональной
пожарной опасности. Приказ МЧС России от 30 июня 2009 г. № 382 // ФГУ ВНИИПО
МЧС России.
– 71 с.
6.
Однолько, А. А. Теория горения и взрыва. Возникновение и
распространение горения. Оценка пожаровзрывоопасности: Курс лекций / А. А.
Однолько, С. А. Колодяжный, Н. А. Старцева. – Воронеж. гос. арх.-строит. ун-т.
– 2-е изд., перераб. и доп. – Воронеж, 2011. – 137 с.
7.
NIST Special
Publication 1026. CFAST – Consolidated Model of Fire Growth and Smoke Transport
(Version 6). Technical Reference Guide. – NIST, 2005. — 92 р. 15.
8.
NIST Special
Publication 1018-5. Fire Dynamics Simulator (Version 5). Technical
Ref-erence Guide. Volume 1: Mathematical Model – NIST, 2008. – 86 p.