Математика / 5. Математическое моделирование

Крючин О.В.

Тамбовский государственный универсистет им. Г.Р. державина

Прогнозирование временных рядов: методы анализа выборки используемой при обучении искусственных нейронных сетей

Искусственные нейронные сети (ИНС) успешно зарекомендовали себя как один из подходов в моделировании различных процессов [1, 2]. Если динамику исследуемого процесса представить в виде временного ряда (ВР) [3], прогнозируемого ИНС, то задачу прогнозирования можно рассматривать как задачу распознавания образов, тогда ИНС будет являться универсальным аппроксиматором дискретной функции, задаваемой набором образов обучающей выборки (ОВ). Качество модели будет зависеть от достоверности исходных данных и способа формирования ОВ [2]. Дополнительным преобразованием ВР, позволяющим улучшить качество прогноза, проводимого с помощью аппарата ИНС, является преобразование пространства классов. Преобразование классов осуществляется за счет трансформации пространства классов путем их параллельного переноса. Данное преобразование позволяет свести к минимуму неопределенность на границах классов и определить с максимальной точностью принадлежность спрогнозированных значений тому или иному классу.

При увеличении разнесения классов в пространстве будет увеличена ошибка прогнозирования, при снижении, невозможно определить нижнюю границу.

После проведения прогноза необходимо определить принадлежность спрогнозированного значения одному из заданных классов. Если значение, полученное в результате прогноза, не попадает ни в один из выделенных классов, это значение включается в ближайший.

Часто элементы векторов-образов являются вещественными (действительными) числами. В этом случае в результате округления или каких-либо других операций на этапе предварительной обработки ОВ, значения элементов могут незначительно отклониться от первоначального значения. Исходя из этого следует ввести вектор допустимых отклонений , размерность которого () соответствует размерности векторов-образов. Необходимость наличия значений обусловлена тем, что различные параметры образов могут иметь различные типы (и соответственно допускать различные отклонения).

Таким образом, образы и будем называть эквивалентными в случае, если условие (1) выполняется для каждого элемента .

(1)

где — допустимое отклонение -го элемента образа.

Повторяемость ОВ определяется количеством эквивалентных образов, содержащихся в классе .

Коэффициентом повторяемости можно назвать величину прямо пропорциональную количеству эквивалентных образов в классе и обратно пропорциональную общему количеству образов в классе. Таким образом, коэффициент повто

ряемости в можно выразить по формуле

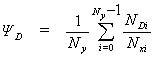(2)

Здесь — общее количество образов в -ом классе, — количество эквивалентных образов в -ом классе, — количество классов.

Полнота ОВ определяет соотношение количества показателей класса и количество образов, содержащихся в нем. Таким образом, -ый класс можно назвать полным, если для него выполняется условие (3)

(3)

где — коэффициент, определяющий количество образов, которое должно соответствовать одному показателю класса (значение данного коэффициента зависит от конкретной задачи, рекомендуется 3-5), — количество показателей класса (количество столбцов выходной выборки).

Исходя из формулы (3) коэффициент полноты ОВ может быть вычислен следующим образом:

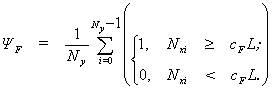(4)

Противоречивыми можно назвать эквивалентные образы, принадлежащие к различным классам. Таким образом, коэффициент противоречивости может быть вычислен по формуле

(5)

где — количество строк в обучающей выборке, — количество противоречивых образов [4].

Средние суммарные показатели (ССП) повторяемости и противоречивости ОВ точно характеризуют процентное соотношение количества одинаковых образов в одних и тех же (повторяемость) и различных (противоречивость) классах.

Количественно ССП повторяемости ОВ может быть вычислено по формуле

(6)

Для расчета СПП противоречивости и повторяемости ОВ необходимо ввести понятие повторяемость входных векторов, которое равно количеству дублируемых строк в наборе входных векторов, тогда ССП противоречивости ОВ

(7)

В результате проделанной работы были введены понятия, позволяющие адекватно и однозначно судить о качестве ОВ, вне зависимости от количества классов ее составляющих. Вычислительный эксперимент показал, что предварительный анализ ОВ с использованием СПП повторяемости и противоречивости целесообразен и необходим. Предварительная оценка качества ОВ позволяет заранее судить о возможности качественного прогноза на конкретных данных.

Литература

1. Anil K. Jain, Jianchang Mao, K.M. Mohiuddin Artificial Neural Networks: A Tutorial, Computer, Vol.29, No.3, March/1996, pp. 31-44.

2. Осовский С. Нейронные сети для обработки информации // Пер. с польского И.Д. Рудинского. М.:Финансы и статистика, 2002. -344 с: ил.

3. Бриллинждер, Д. Временные ряды. -М.: Мир. 1980-536 с.

4. Тарасенко Р.А., Крисилов В.А. Предварительная оценка качества обучающей выборки для нейронных сетей в задачах прогнозирования временных рядов // Труды Одесского политехнического университета – 2001 Вып.1 (13) – с. 90-93.