Д.ф.-м.н. Срумова Ф.В.

Таджикский национальный университет

ФУНКЦИОНАЛ ЭНЕРГИИ ДЛЯ АБСТРАКТНОЙ ПРОБЛЕМЫ КОШИ

Вычислена асимптотика при энергии для решения абстрактной задачи Коши. Рассмотрен пример вычисления асимптотики энергии при для абстрактного волнового уравнения и для волновода.

Ключевые слова: гильбертово пространство - абстрактная проблема Коши.

Пусть -комплексное гильбертово пространство со скалярным произведением . Рассмотрим абстрактную задачу Коши

(1)

где -самосопряженный оператор с областью определения . Тогда -решение задачи (1). Энергией для решения задачи (1) назовем функцию

Рассмотрим следующую задачу Коши:

(2)

Ее решение имеет вид

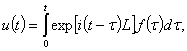
где интеграл понимается в смысле Бохнера, т.е. как предел по норме интегральных сумм вида

Назовем энергией для решения задачи (2) функцию

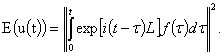
Лемма 1. Если то энергия решения задачи (2) может быть вычислена по формуле

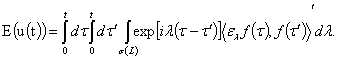
Доказательство. Согласно определению скалярного произведения в имеем

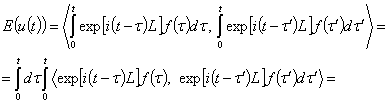
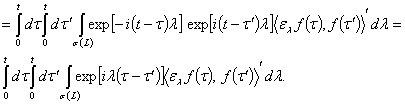
Лемма 2. Пусть -спектральная функция оператора и абсолютно непрерывная функция относительно меры Лебега,

тогда

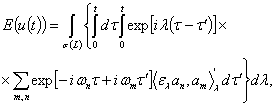
где -спектр оператора

Теорема 1. Пусть для всех и -точка Лебега функции Тогда

(3)

Доказательство. Из лемм 1 и 2 следует, что

Преобразуем следующим образом (см. [1]):

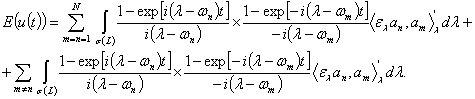
Пусть тогда

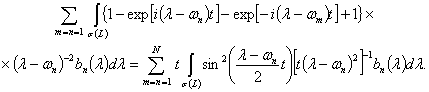(4)

На основании теоремы о ядрах типа Фейера (см. [2]), при из (4) получим

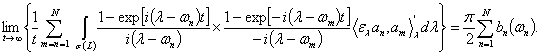(5)

Пусть тогда

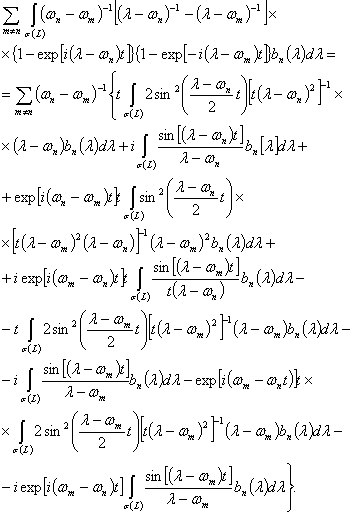(6)

Из (6), аналогично тому как это делалось при , получаем, что при справедливо

(7)

Объединяя (5) и (7), приходим к равенству (3).

Пример 1. Пусть -гильбертово пространство со скалярным произведением (,), - самосопряженный, положительно-определенный оператор в , - положительный квадратный корень из оператора .

В пространстве рассмотрим абстрактное волновое уравнение.

(8)

Покажем, как задачу (8) можно свести к уже рассмотренной нами. Для этого введем гильбертово пространство со скалярным произведением

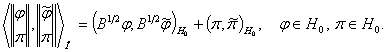
Рассмотрим абстрактную задачу

(9)

Здесь

самосопряженный в оператор с областью определения

Задача (9) эквивалентна (8), решение которой задается формулой

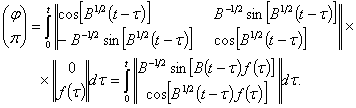
Энергией для решения задачи (9) называется величина

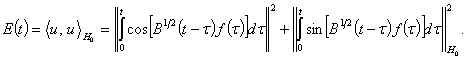(10)

Заметим, что в (10) входит оператор и норма в пространстве , поэтому удобно получить асимптотику энергии именно в терминах оператора (можно построить спектральную функцию оператора и воспользоваться предыдущими результатами).

Лемма 3. Справедливо равенство

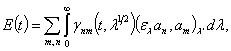
где

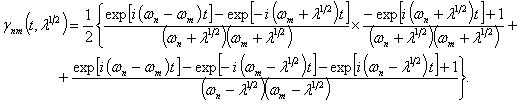
Теорема 2. Пусть для всех точка Лебега функции , тогда

(11)

Доказательство. Лемма 3 утверждает, что

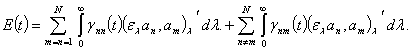(12)

Разделив (12) на и перейдя к пределу при , получим (11).

2. Пусть -гильбертово пространство со скалярным произведением (,), самосопряженный, положительно-определенный оператор в -положительный квадратный корень из

В пространстве рассмотрим абстрактное волновое уравнение

(13)

Введем в качестве гильбертово пространство со скалярным произведением

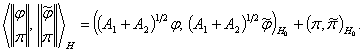
Поставим абстрактную задачу:

(14)

Где -самосопряженный в оператор с областью определения

Задачи (13) и (14) эквивалентны.

Решение задачи (13) примет вид

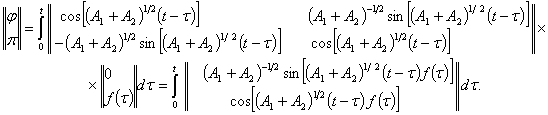
Энергия для решения задачи (14) представима в виде

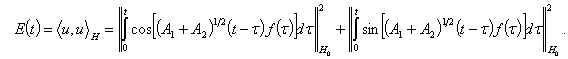
Лемма 4. Пусть -спектральная функция оператора и является абсолютно непрерывной функцией относительно меры Лебега:

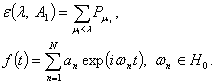
Тогда

где

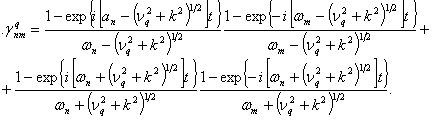
Теорема 3. Пусть для всех и -точка Лебега функции ; тогда

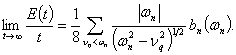
Л И Т Е Р А Т У Р А

1. Арсеньев А.А. О поведении энергии решения волнового уравнения при больших временах.-Ж. вычисл. матем. и матем. физ., 1970, т. 10, №4, с. 1037-1041.

2. Ахиезер Н.И. Лекции по теории аппроксимации. М.: Наука, 1965.