Маркерт Валентина Степановна,
учитель математики
Казахстан, Костанайская область, Затобольская средяя школа № 2
Параллелограмм.
(8 класс, геометрия.)
Цель:
Образовательная:
обобщить и систематизировать знания
признаков и свойств параллелограмма; умения решать задачи на применение свойств.
Развивающая: способствовать развитию математической речи,
логического мышления, умению делать выводы.
Воспитательная: способствовать воспитанию сотрудничества, «чувства
локтя», уверенности в себе и индивидуальной ответственности за достижение
результата.
Оборудование: интерактивная доска, слайды презентации. тесты,
бумажные модели
параллелограмма.
Тип
урока: урок обобщения знаний.
«Геометрия является самым могущественным средством для
изощрения наших умственных способностей и дает нам возможность правильно мыслить и
рассуждать»
Г. Галилей
План урока:
I.
Оргмомент.
II. Проверка
домашнего задания.
III. Актуализация знаний.
IV.
Практическая работа.
V. Домашнее
задание.
VI. Закрепление
умений применять свойства к решению задач.
VII.
Тестирование.
VIII. Итог урока.
IX. Рефлексия.
Ход урока:
I. Оргмомент. Ребята, урок я начну с высказывания Г.Галилея:
«Геометрия является самым могущественным средством для изощрения наших
умственных способностей и дает нам возможность правильно мыслить и рассуждать».
Я хочу, чтобы вы на уроке думали и
рассуждали. Сегодняшний урок геометрии – урок обобщения знаний. Вы, ребята,
должны знать определение параллелограмма, свойства и признаки параллелограмма.
Будем учиться пользоваться свойствами и признаками при решении задач.
II. Проверка домашнего задания.
III.Актуализация знаний. (Слайд 4-6)
Устно: проверка теоретических знаний
1)
Что называется
параллелограммом?
2)
Какие свойства
параллелограмма вы знаете?
3)
Какие признаки
параллелограмма вы знаете?
4)
Существует еще ряд
свойств параллелограмма. Ободном из них вам расскажет и докажет
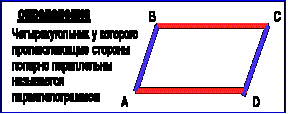

Теорема: Биссектриса угла параллелограмма отсекает от
него равнобедренный треугольник.
Теорема доказывается учащимся с помощью интерактивной
доски. (Слайд 6) Учащиеся делают записи в тетради.
IV.Практическая работа.
Продолжаем рассматривать свойства параллелограмма. У
каждого из вас на столе лежит бумажный макет параллелограмма. Методом оригами
(метод сгиба) определим биссектрису каждого из четырех углов.
Учащиеся выполняют практическую работу (можно в паре).
Что получилось в пересечении биссектрис? Предполагаемые
ответы: квадрат, прямоугольник, четырехугольник…
Проверим с помощью чертежного угольника углы
получившегося четырехугольника. Вывод: углы прямые.
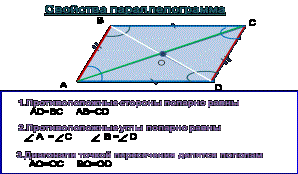
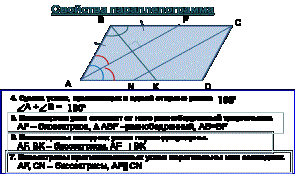
Свойства
параллелограмма: Биссектрисы соседних
вершин параллелограмма пересекаются под прямым углом.
Биссектрисы противоположных вершин параллелограмма
параллельны.
V. Домашнее задание: (Слайд 7)1) Доказать, что
биссектрисы соседних вершин параллелограмма пересекаются под прямым углом.
2) №28. (Открыть учебник, прочитать задачу. Какие
вопросы?)
VI. Закрепление умений применять свойства к решению
задач.
Решение задач по готовым чертежам.
№1
устно. Ответ: 64![]() , 116
, 116![]() (Слайд
8) №2
устно. Ответ: 65
(Слайд
8) №2
устно. Ответ: 65![]() и 115
и 115![]() (Слайд
8)
(Слайд
8)
№3 у
доски. Ответ: 10см и 4см.(Слайд
9) №4
у доски. Ответ: Р=16см.(Слайд
9)
VII. Тест (2
варианта) на листах через копировальную бумагу, оригинал сдать, взаимопроверка
+ оценка.
VIII. Итог урока.
IX. Рефлексия. (Слайд 10) На макетах параллелограммов поделитесь мыслями о
сегодняшнем уроке:
Я узнал….
Я хочу узнать…
Я могу помочь…
Я сначала испугался, а потом…
Я заметил, что…
Я так и не понял…
Знания, полученные на уроке, мне пригодятся…