На конфер. «Современ. науч. достиж. – 2014», в рубрики:

строительные материалы /химические технологии

Инж. Мирошников В.П., инж. Храпов А.А., д.т.н. Полтавцев В.И.

Кемеровский Государственный сельскохозяйственный институт, Россия

Кинетика каркасообразования при смерзании

круглого ледяного гранулята

В статье отражены результаты исследований кинетики процесса адиабатического смерзания круглых ледяных шариков одинакового диаметра при математическом моделировании намораживания льда как задачи Стефана со свободной границей фазового перехода и при экспериментальных исследованиях с погружением фигур из соприкасающихя шариков в воду [1,2]. Температура воды постоянна - 0⁰С, воздуха (и льда) – варьировалась в диапазоне (-10...-38 ⁰С). Диаметр шариков 26,5 мм.

На рис. 1 и 2 фрагменты пошагового экспериментального намораживания (фото) для 2, 3 и 4 шаров, соответственно. Измерялись диаметры шаров, их перемычек, радиусы закругления и углы щели между гранулами после погружений в воду. Получены эмпирические зависимости массы и перечисленных геометрических параметров от времени и шага наморозки льда на фигуры.

Рис. 1 - фрагменты пошагового смораживания 2-х и 3-х шаров

Предложена и численно реализована двухмерная осесимметричная математическая модель смерзания двух и цепочки гранул в обобщенной формулировке задачи Стефана, когда условие Стефана на подвижной границе фазового перехода включено в само уравнение теплопроводности.

Ее численное решение основано на методе расщепления по пространственным переменным, замене дифференциального уравнения разностным аналогом и методе сеток. Реализация конечно – разностной схемы проводится методом прогонки.

Рис. 2 – смерзание 4-х шаров

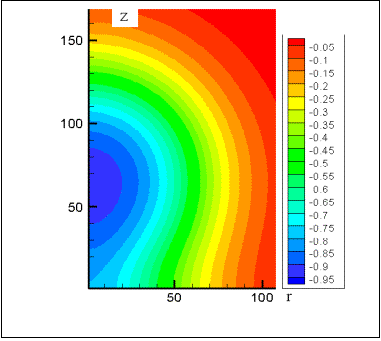На рис. 3 изображена пошаговая компьютерная зарисовка наморозки льда для двух соприкасающихся шаров в первом квадранте Декартовой системы координат Z, r (ввиду осевых симметрий фигуры).

Рис. 3 - компьютерная зарисовка пошаговой наморозки на правый верхний полушар при смерзании двух шаров

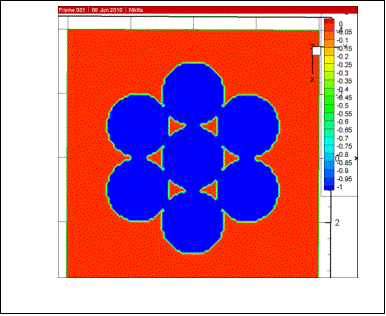
Трехмерная модель и ее численная реализация [3] предложены для частного случая - плоской конфигурации «солнышко» (один шар касается в плоскости 6 шаров (рис. 4)).

В трехмерном пространстве каждый непограничный шар касается не более 12 таких же шаров (известная задача об упаковках). Причем остается свободное место для проскальзывания этих 12 шаров между собой.

Поэтому граничные условия и математическую модель при насыпной плотности шаров записать не удается. Но в эксперименте орошение гранулята водой хорошо иллюстрирует аналогичную приведенным компьютерным зарисовкам кинетику смерзания.

Рис. 4 – Первый шаг наморозки на касающиеся в плоскости 7 шаров

Как наглядно свидетельствуют рисунки 1 – 4, математическая модель процесса намораживания и ее численная реализация выбраны адекватно, экспериментальные исследования его кинетики повторяют геометрию наморозки при численной реализации.

Способ быстрого двухстадийного намораживания прочного ледового покрытия речных переправ [5] основан на исследованиях кинетики первой стадии – мгновенного каркасообразования при адиабатическом смерзании круглого ледяного гранулята при первом орошении водой за счет холода гранул. Математические расчеты и экспериментальное подтверждение оптимального объема воды орошения приведено в работе [4].

Литература:

1. Мирошников, П. В. Бимерное адиабатическое смерзание сферических гранул льда / П. В. Мирошников, В. И. Полтавцев, В. В. Рагулин // Вестник международной академии холода. - Санкт-Петербург - Москва. - 2008. - вып. 4. - С. 42-45.

2. Мирошников, П.В. Замораживание сферического гранулята льда в воде, математическая модель и алгоритм численного решения задачи Стефана / П.В. Мирошников, В.В. Рагулин, В.И. Полтавцев // Пути повышения эффективности сельскохозяйственного производства в Сибирском регионе: Сб. науч. статей. Материалы международной научно – практической конференции, посвящённой 50 – летию Тюменской государственной сельскохозяйственной академии / Вестник ТГСХА – Тюмень, 2009. – Вып.3. – С. 164 – 167.

3. Мирошников, П.В. Моделирование смерзания ледяного гранулята в воде // П.В. Мирошников, В.В. Рагулин, В.И. Полтавцев // Краевые задачи и математическое моделирование: сб. науч. ст.: в 3 т. Т. 2. / НФИ ГОУ ВПО «КемГУ». – Новокузнецк, 2010. – с.32-33.

4. Мирошников, П.В. Стабилизация каркаса в слое ледяных гранул / П.В. Мирошников, В.В. Рагулин, В.И. Полтавцев // Вестник КемГУ, вып. № 4 (52) Т.1, 2012. – Кемерово, изд-во КемГУ, 2012. – С. 271 – 274.

5. Заявка на патент «Способ намораживания ледовых покрытий», № 2013137093 от 06.08.13 г.