А. И. Федотов д.т.н.,
С.К. Лисин к.т.н.
СПб государственный политехнический университет, СПб
национальный минерально-сырьевой университет «Горный», Россия
ИССЛЕДОВАНИЕ ПАРАМЕТРОВ
НЕЛИНЕЙНЫХ ДИНАМИЧЕСКИХ
СИСТЕМ
В связи с ужесточением требований к качеству и конкуренто-способности
продукции возникла необходимость совершенствования и развития методов и средств
измерений, базирующихся на проведении исследований динамических режимов,
которые способствуют повышению точности и ресурса. Применение подвижных систем,
подвергнутых динамическому анализу, позволяет расширить области применения вибрационных,
виброконтактных и других средств измерений, взаимодействующих с объектом
контроля. Подобные подвижные системы и их элементы находят применение в
устройствах релейных систем, промышленных роботов, специальных приспособлений,
оснащаемых приборами и преобразователями электромеханического типа.
Например, измерения перемещений и отклонений длин в ходе технологических
процессов и при автоматизации измерений
могут быть выполнены средствами, реализующими режимы периодического
взаимодействия с объектом контроля.
В рамках современных микро - и нано - технологий необходимо развитие
методов и средств не только контроля перемещений, отклонений длин, износа
движущихся поверхностей, но и контроля физико-механических свойств изделий.
Непосредственное применение средств контроля контактного типа осуществляется
для неподвижных или медленно движущихся изделий. Именно поэтому в последнее
время стали актуальными задачи, касающиеся исследования,
проектирования и применения вибрационных, виброконтактных и контактных
измерительных приборов и преобразователей. Исследования различных по своей
физической природе измерительных систем, оказывают непосредственное влияние на
развитие техники измерения процессов нелинейных колебаний [1,2]. При этом качество средств
контроля определяется адекватностью
моделирования режимов, параметры которых находятся в определенной зависимости
от свойств системы «измерительный наконечник –
объект контроля»
[3-6].
Анализ
результатов экспериментальных исследований показал, что контроль локальных
физико-механических свойств изделий целесообразно производить на частоте
основного резонанса. При этом появляется возможность представить зависимость параметра
локальной жесткости от амплитуды колебаний.
Такой подход упрощает не только
математическую модель процесса колебаний, но и позволяет выявить влияние
жесткости контролируемого изделия на амплитуду и смещение центра колебаний
системы относительно положения статического равновесия при меньшем числе
параметров.
Динамическая характеристика рассматриваемой
виброконтактной системы может быть представлена в безразмерных переменных
кусочно-линейной функцией
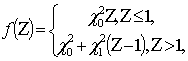 (1)
(1)
где
![]() – абсолютная величина
перемещения измерительного наконечника относительно его положения статического
равновесия;
– абсолютная величина
перемещения измерительного наконечника относительно его положения статического
равновесия;
![]() ;
;![]() ; m
– масса измерительного наконечника;
; m
– масса измерительного наконечника;
с1
,с2 – жесткости упругого подвеса и объекта контроля;
w - круговая частота.
Первое
уравнение (1) соответствует фазе движения измерительного наконечника без
контакта с поверхностью изделия, а второе уравнение – фазе движения измерительного
наконечника в контакте с поверхностью изделия.
Математическая
модель кусочно-линейной системы с одной степенью свободы, описывающая режим
одночастотных колебаний, будет иметь вид
![]() ,
(2)
,
(2)
где![]() - амплитуда возмущающего воздействия;
- амплитуда возмущающего воздействия;
![]() - безразмерное время.
- безразмерное время.
Поскольку все члены (2) являются
периодическими, искомое решение режима одночастотных колебаний будет также
периодическим с фиксированной частотой возмущающей силы. Поэтому можно
предположить, что приближенное периодическое решение следует искать с помощью универсального
для малых колебаний метода гармонического баланса. В соответствии с методом гармонического баланса периодическое
решение для системы, динамическая характеристика которой несимметрична
относительно начала координат, записывается в виде
![]() , (3)
, (3)
где
![]() ,
, ![]() – амплитуда и
смещение центра колебаний соответственно;
– амплитуда и
смещение центра колебаний соответственно;
В последнее время метод гармонического
баланса широко используется для нахождения приближенных периодических решений
нелинейных дифференциальных уравнений с помощью коэффициентов Фурье
линеаризованной характеристики. При этом из (2) получим соотношения
![]() , (4)
, (4)
![]() . (5)
. (5)
Уравнения (4), (5) совместно с
результатами интегрирования уравнений (3) методом гармонического баланса по
переменной ![]() позволяют получить
замкнутую систему трансцендентных уравнений, устанавливающих связь между
амплитудой
позволяют получить
замкнутую систему трансцендентных уравнений, устанавливающих связь между
амплитудой ![]() , смещением центра колебаний
, смещением центра колебаний ![]() и фазовым параметром
и фазовым параметром ![]()
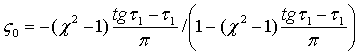 , (6)
, (6)
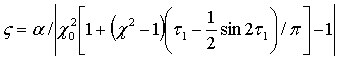 , (7)
, (7)
![]() , (8)
, (8)
где ![]() - параметр локальной
жесткости изделия
- параметр локальной
жесткости изделия ![]() .
.
Параметр ![]() соответствует времени
выхода измерительного органа из фазы контакта и определяет его длительность.
При
соответствует времени
выхода измерительного органа из фазы контакта и определяет его длительность.
При ![]() нелинейная система
(6), (7), (18) становится линейной и переходит в вибрационный режим (
нелинейная система
(6), (7), (18) становится линейной и переходит в вибрационный режим (![]() 0=0).
Значения
0=0).
Значения ![]() и
и ![]() 0=0 соответствуют
амплитуде вибрационного режима, равной величине зазора системы в направлении
линии измерения.
0=0 соответствуют
амплитуде вибрационного режима, равной величине зазора системы в направлении
линии измерения.
Нелинейная восстанавливающая сила,
действующая на измерительный наконечник при его контактировании в периодическом
режиме с объектом контроля, определяет нелинейность виброконтактной системы в
целом. В вибрационном режиме подвижная система действует как нелинейный
гармонический осциллятор. Для обеспечения малого измерительного усилия упругий
подвес указанной подвижной системы имеет соответствующую по величине
восстанавливающую силу в диапазоне xmin≤x≤![]() . В виброконтактном режиме измерительный наконечник
контактирует с объектом контроля при величине зазора
. В виброконтактном режиме измерительный наконечник
контактирует с объектом контроля при величине зазора ![]() >1 между измеряемой поверхностью и положением
статического равновесия.
>1 между измеряемой поверхностью и положением
статического равновесия.
Полученная
методом гармонического баланса математическая модель позволяет установить
аналитическую зависимость между амплитудой виброконтактной системы и
механическими свойствами объекта контроля. При этом подтверждается возможность
осуществления контроля механических свойств с помощью виброконтактного метода. При
этом шкала отсчетного устройства виброконтактного преобразователя может быть
аттестована в единицах твердости [7]. Жесткость изделия выражается через
жесткость меры твердости, естественно, в единицах твердости шкал Бринелля,
Роквелла, Виккерса, Шора.
Литература:
1. Боголюбов
Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний.
- М.: Наука, 1974. - 504 с.
2. Андронов А.А., Витт А.А., Хайкин
С.Э. Теория колебаний. -
М.: Наука, 1981. - 568 с.
3. Бундур М.С. Повышение эксплуатационно -
технических характеристик технологического оборудования/ М.С. Бундур, В.А.
Прокопенко, Н.А.Пелевин// Научно – технические ведомости. – 2012 - № 4.- С.121-127.
4. Лисин, С.К. Технические измерения /С.К. Лисин,
А.И. Федотов. – СПб.: Изд-во НМСУ «Горный», 2012. – 66 с.
5.
Федотов, А.И. Применение нелинейной теории минимизации в прикладных задачах
синтеза свойств объектов/ А.И. Федотов, С.К. Лисин // Научно-технические
ведомости. – СПб.: Изд-во СПбГПУ, 2012. - № 3(153). – С. 133 – 135.
6.
Козлов В.Н. Децентрализованная стабилизация параметрических возмущенных
крупномасштабных систем/ В.Н. Козлов, В.Н. Шашихин// Научно –
технические ведомости. – 1996. - № 1. -
С. 62-65.
7. Астров Д.Н., Бацанов С.С., Бригадзе Ю.И.и др.. Соврменные
метрологические проблемы физико-технических измерений. / Под ред. Коробова В.К.
– М.: Изд. стандартов, 1988. -320 с.