Малоземов А.В.

Томский государственный университет, Россия

ИССЛЕДОВАНИЕ ДЕФОРМАЦИИ ДЕТАЛЕЙ МЕХАНИЗМА

Математическая модель деформаций

По аналогии с задачами о потенциальном течении жидкости рассмотрены процессы деформации в прямоугольной области занятой несжимаемым упругим материалом. Такие процессы имеют место и являются важными в задачах контактного взаимодействия деталей механических систем в условиях наличия и эффективного действия в них смазочных материалов, когда касательные напряжения являются минимальными, а нормальные напряжения играют определяющую роль в распределении усилий в системе. Особую важность приобретают задачи о периодическом взаимодействии деталей системы, что, например, имеет место в системах передачи движения (трансмиссии, редукторы, и т.д.) поскольку от частоты и интенсивности таких воздействий зависит надежность и долговечность работы системы.

Рассматривается несжимаемая среда и введенный в рассмотрение потенциал перемещений Φ. По теореме разложения Гельмгольца, всякую деформацию можно представить как сумму объемной деформации, определяемой потенциалом перемещений Φ, и деформации сдвига, определяемой вектором . Задачи на определение деформаций сдвига решаются с помощью нахождения компонент рассматриваемого вектора, каждая из которых удовлетворяет уравнению Лапласа. Кроме этого, по аналогии с задачами динамики жидкости, потребуется ввести в рассмотрение аналог функции тока или векторного потенциала, компоненты которого будут удовлетворять уравнениям Пуассона. После решения вопроса с граничными условиями для упомянутых функций можно найти сдвиговые деформации, например, в задачах кручения или комплексных задачах на сжатие и сдвиг, и далее, используя принцип суперпозиции решения (утверждение, обратное теореме Гельмгольца), найти решение полной задачи.

В линейной теории упругости задача определения объемных деформаций может быть отделена от задачи расчета деформаций сдвига, что и сделано в настоящей работе. Поэтому ниже будет рассмотрена задача, связанная с нахождением потенциала перемещений Φ в прямоугольной области, одна из границ которой является свободной.

Предположим, что потенциал перемещений найден. Тогда можно найти вектор перемещений V, то есть все его компоненты u, v, w. Так же в механике известны соотношения Коши [1, 3], которые определяют компоненты тензора деформаций через перемещения. Далее используя обобщённый закон Гука[2], представляется возможным найти компонент тензора напряжений.

Решение задачи расчета Φ будем строить итерационно-разностным методом, то есть с использованием простейших симметричных аппроксимаций для вторых производных и метода простой итерации для перерасчета значений искомой величины в узлах разностной сетки.

На этапе численной реализации предварительно проводились следующие тесты:

Тривиальный тест. При и всех других описанных выше граничных условиях, получаются нулевые распределения для всех компонентов перемещений.

Баланс массы. Поскольку материал является несжимаемым, то свободная поверхность должна деформироваться таким образом, что бы объем ограниченный этой поверхностью оставался неизменным.

Представленные ниже данные получены на сетке узлов, при 20000 глобальных итерациях. При этом, расчетный баланс массы имеет погрешность 0.2%.

Ниже в качестве примера применения описанной схемы расчета представлены результаты сжатия упругого куба с ребром 0,2 м недеформируемым кубическим элементом с ребром 0,04 м. Предполагалось, что рассматривается металлический объект, характеризующийся коэффициентом Пуассона ν = 0,3. Деформации металлических образцов, происходящие в упругом режиме, составляют всего доли процентов от линейных размеров объекта. Заметим, что математическая постановка задачи допускает использование линейных размеров объекта в системе СИ, то есть в метрах, а рассчитывать перемещения в технических единицах, то есть в данном случае в микронах.

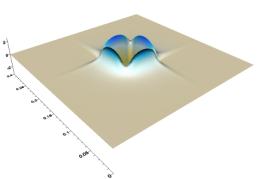
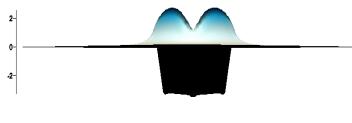
Рис. 1. Распределения вертикальной компоненты перемещения на свободой поверхности бассейна

Вывод

В работе предложена схема расчета потенциальных деформаций упругих тел, основанная на введении потенциала перемещений.

Предложена итерационно-разностная вычислительная технология реализации поставленной задачи, главными особенностями которой является простота и универсальность.

Получено решение задачи о деформировании параллелепипеда и его свободной поверхности под воздействием абсолютно жесткого элемента. Литература:

1. Демидов С.П. Теория упругости. – М. : Высшая школа, 1979. – 340 с.

2. Хан Х. Теория упругости. Основы линейной теории и ее применения. – М. : Мир, 1988. – 344 с.

3. Ляв А. Математическая теория упругости. – М.-Л. : Главная редакция общетехнической литературы и номографии, 1935. – 674 с.