Технические
науки/2. Механика
Д.т.н.
Боронко О.А., магистрант Лабунский А.В.
Национальный технический университет Украины «Киевский
политехнический институт», Украина
Модифицированный метод покоординатного спуска к
определение собственных частот и собственных форм колебаний машиностроительных
конструкций
Одной из важнейших задач при расчете колебаний упругих
систем является определение собственных частот и соответствующих им собственных
форм колебаний. Аналитическое решение данной задачи возможно лишь для
ограниченного круга задач. Поэтому возникает необходимость численного
определения частот и собственных форм колебаний, при этом приходится
ограничивать число разыскиваемых собственных частот и соответствующих им форм
колебаний. На практике, как правило, при расчете конструкции или ее элементов,
подверженных действию вибрационных нагрузок необходимо знать до 20 первых
собственных частот и соответствующих им собственных форм колебаний. В целом
проблема их отыскания при решении задач о вынужденных колебаниях реальных
механических систем весьма трудоемка и требует больших временных затрат даже
при наличии современных ЭВМ. Поэтому задача создания и развития алгоритмов
определения собственных частот и соответствующих им собственных форм колебаний
упругих систем является актуальной [1].
Машиностроительные конструкции и их конструктивные
элементы являются сплошными телами.
Из
вариационного принципа для нелинейных свободных колебаний следует, что если
характеристики движения изменяются периодически c частотой ω, то
существует функционал [2], [3] :
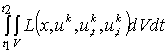 , (1)
, (1)
точки
стационарности которого соответствуют действительным движениям тела, при
заданных граничных условиях (например ![]() на
на ![]() ).
).
Если в качестве промежутка времени взять один период ![]() , то функционал
примет вид:
, то функционал
примет вид: ![]()
![]()
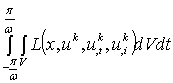 , (.2)
, (.2)
при условии 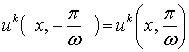 .
.
Если сделать
замену ![]() , то получим
, то получим ![]() . (3)
. (3)
Если лагранжиан равен L=K – U,
где K![]() 0 – кинетическая энергия , U
0 – кинетическая энергия , U![]() 0 – потенциальная энергия и K – однородная функция второй степени по
0 – потенциальная энергия и K – однородная функция второй степени по ![]() , т.е. для любого ω
> 0
, т.е. для любого ω
> 0
![]() . (4)
. (4)
Причем K и U строго выпуклы по
совокупности своих аргументов и выполняется условие:
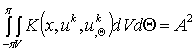 , (5)
, (5)
где А – постоянная, то используя метод
неопределенных множителей Лагранжа придём к функционалу
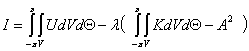 , (6)
, (6)
где λ – множитель
Лагранжа. Стационарная точка
функционала имеет место при ![]() . Если
. Если ![]() , то после интегрирования по времени функционал примет вид:
, то после интегрирования по времени функционал примет вид:
![]() , (7)
, (7)
где ![]() и
и![]() - квадратичные
формы:
- квадратичные
формы:
![]() , (8)
, (8)
![]() , (9)
, (9)
и являются амплитудами потенциальной и кинетической энергий.
В работе итерационный процесс строится следующим образом:
![]() , где
, где ![]() - вектор узловых
неизвестных,
- вектор узловых
неизвестных, ![]() - единичный вектор
в направлении
- единичный вектор
в направлении ![]() ,
, ![]() - шаг. Функционал в k+1 приближении образом записывается в
виде:
- шаг. Функционал в k+1 приближении образом записывается в
виде:
![]() , (10)
, (10)
где 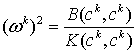 , а
, а ![]() - данная величина
может быть истолкована как сила
инерции, тогда функционал примет вид
- данная величина
может быть истолкована как сила
инерции, тогда функционал примет вид
![]() , (11)
, (11)
в результате функционал примет вид:
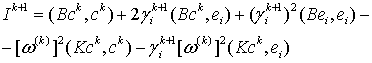 (12)
(12)
Приращение функционала на k+1 приближении равно
![]()
![]() (13)
(13)
Величина шага определяется из
условия максимальной скорости уменьшения ![]()
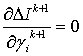 , (14)
, (14)
тогда
![]()
![]() , (15)
, (15)
отсюда величина шага определяется следующим соотношением
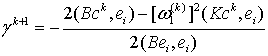 (16)
(16)
Таким образом итерационный процесс упрощается и конечная формула для
определения шага имеет туже структуру , что и для статической задачи. Вторая
собственная форма колебаний и собственная частота определяются на
подпространстве, ортогональном первой собственной форме колебаний. Вектор,
ортогональный первой собственной форме колебаний определяется соотношением:
![]() , (17)
, (17)
где ![]() - нормированный
собственный вектор, соответствующий первой собственной частоте. Тогда величина
шага при переходе в k+ 1 приближении
запишется:
- нормированный
собственный вектор, соответствующий первой собственной частоте. Тогда величина
шага при переходе в k+ 1 приближении
запишется:
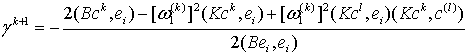 , (18)
, (18)
аналогично определяется шаг при нахождении высших собственных частот и
соответствующих им форм колебаний
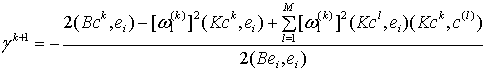 .(19)
.(19)
где ![]() квадрат круговой l-й
собственной частоты,
квадрат круговой l-й
собственной частоты, ![]() - l-я собственная форма колебаний,
- l-я собственная форма колебаний, ![]() - число определяемых собственных частот и соответствующих им
собственных форм колебаний. Таким образом решая систему (14) и применяя
отношение Релея-Ритца определяется необходимое число собственных частот и
соответствующих им собственных форм колебаний.
- число определяемых собственных частот и соответствующих им
собственных форм колебаний. Таким образом решая систему (14) и применяя
отношение Релея-Ритца определяется необходимое число собственных частот и
соответствующих им собственных форм колебаний.
Для ускорения сходимости итерационного процесса
использовался метод неполной релаксации в котором ![]() приближения строилось
в виде:
приближения строилось
в виде:
|
|
(20) |
где ![]() - параметр
релаксации. Оптимальный параметр релаксации
- параметр
релаксации. Оптимальный параметр релаксации ![]() выбирается на
основании работы [4].
выбирается на
основании работы [4].
В качестве критерия останова итерационного процесса
использовалось следующее условие:
|
|
(21) |
где ![]() - наперед заданная
малая постоянная.
- наперед заданная
малая постоянная.
Для
реализации предложенного метода
были разработаны
вычислительные программы определения собственных частот и соответствующих им собственных форм
колебаний, при продольных, крутильных и изгибных колебаниях стержней при
продольных и изгибных колебаниях пластин, при свободных колебаниях
пластинчато-оболочечных конструкций, а также при колебаниях трехмерных тел.
Решение тестовых и практических задач показало, что
процесс сходится и позволяет с заданной точностью определить собственные
частоты и соответствующие им собственные формы колебаний [4].
Следует также отметить, что по сравнению с
традиционным подходом минимизации отношения Релея-Ритца методом покоординатного
спуска, для нахождения собственных частот и соответствующих форм колебаний,
данный подход позволил в несколько раз уменьшить время решения задач, что
весьма существенно при решении прикладных задач.
Литература:
1. Ильин
В.П. Численные методы решения задач
электрофмзики. – М: Наука. Главная редакция физико-математической
литературы, 1985.- 336 с.
2. Марчук
Г.И., Кузнецов Ю.А. Итерационные методы и квадратичные функционалы.
Новосибирск:Наука, 1972.-205 с.
3. Михлин
С.Г. Численная реализация вариационных методов.- М.:Наука, 1968.-432 с.
4.
Бабенко А.Е., Бобырь Н.И., Бойко С.Л., Боронко О.А.
Применение и развитие метода покоординатного спуска в задачах
определения напряженно-деформи-рованного состояния при статических и
вибрационных нагрузках К.:
Инрес, 2005.-264с