Технические
науки/2. Механика
К.т.н. Гирнис
С.Р., д.т.н. Украинец В.Н., Алигожина Д.А., Жакиянова А.Х.
Павлодарский государственный
университет, Казахстан
РАСПРОСТРАНЕНИЕ ГАРМОНИЧЕСКИХ ВОЛН В ТРАНСПОРТНЫХ ТРУБОПРОВОДАХ
Задачи об исследовании динамики трубопроводов под воздействием
транспортных нагрузок (подвижных нагрузок, от транспортируемых по ним объектам)
встречаются в технике довольно часто. В частности такие вопросы возникают при
расчете магистральных нефте- и газопроводов, в которых в результате действия
импульсивных периодических возмущений от работающих компрессоров
устанавливается периодическая бегущая волна давления, распространяющаяся со
скоростью движения звука в потоке. Аналогичные явления имеют место в
трубопроводах химических предприятий, гидро- и газовых системах летательных
аппаратов и тепловых энергетических установок, а также при проведении
взрывопрострелочных работ в геотехнологических скважинах.
Весьма специфические эффекты порождаются в трубах,
содержащих детонирующие материалы. Поскольку при инициировании детонации таких
материалов могут генерироваться взрывные ударные волны, имеющие различные
профили и распространяющиеся с различными скоростями. (достигающими две и более
тысяч метров в секунду), важно проанализировать влияние параметров
детонационной волны на динамику трубопровода, содержащего ее. При этом, как
показано ниже могут достигаться критические значения этих параметров, при
которых расчетные величины прогибов трубопровода и возникающие в нем напряжения
в рамках линейной теории неограниченно возрастают.
Для решения задачи о распространении бегущих осесимметричных
волн упругих деформаций в стенке тонкой трубы в [1] использовалась теория оболочек типа Тимошенко. В работе
В.М. Львовского и В.И. Пожуева [2] для докритических скоростей подвижной
осесимметричной нормальной нагрузки проведено исследование рамок применимости
приближенных теорий оболочек (классической и типа Тимошенко) и установлено, что
если отношение толщины оболочки к радиусу ее срединной поверхности меньше 0,05,
то в этом случае можно пользоваться классической теорией оболочек, как наиболее
простой. Поэтому в настоящей статье подобная [1] неосесимметричная задача для тонкостенных трубопроводов,
удовлетворяющих данному критерию, решена на основе классической теории оболочек.
1. Рассмотрим трубопровод в виде тонкой круговой
цилиндрической оболочки радиусом R и толщиной h0 в
цилиндрической системе координат r, q, z, ось z которой совпадает с осью оболочки.
Поставим задачу о распространении в оболочке свободных
неосесимметричных гармонических волн.
Введем фазовую координату h = z – ct, движущуюся со скоростью c. Тогда для описания свободных колебаний оболочки можно
воспользоваться классическими уравнениями теории тонких оболочек [3] в форме
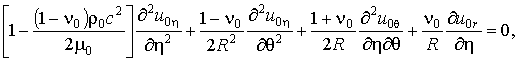
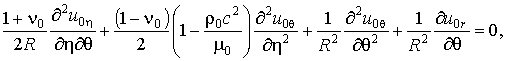 (1)
(1)
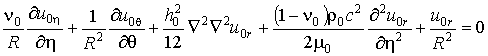 ,
,
где u0h, u0q, u0r – перемещения точек срединной поверхности оболочки; n0, m0, r0 – соответственно коэффициент Пуассона, модуль сдвига и плотность материала оболочки.
Исследуем движение собственных гармонических волн в
оболочке вида
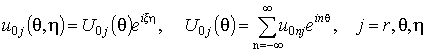 . (2)
. (2)
Подставляя (2) в (1), для n-го члена разложения получим
![]()
![]()
![]() ,
,
где ![]()
![]()
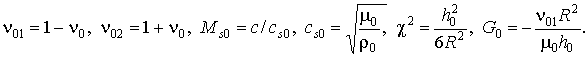
Эта система однородных алгебраических относительно u0nh, u0nq, u0nr, уравнений
имеет нетривиальное решение, когда определитель матрицы ее коэффициентов равен
нулю. Из этого условия следуют дисперсионные уравнения
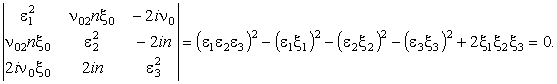 (3)
(3)
Здесь ![]() .
.
Решение дисперсионного уравнения (3) c = c(n)(x(n)) определяет скорости движения n-ой моды собственных гармонических волн вида (2) в цилиндрической оболочке. Как видим, уравнение (3) является уравнением шестой степени относительно c. Однако, учитывая, что c входит в него только в квадрате, это уравнение можно привести к кубическому уравнению относительно c2 и найти три зависимости для фазовых скоростей движения свободных волн ci = c(n)i(x(n)i) (i = 1,2,3).
При n = 0 уравнение
(3) перепишется в виде
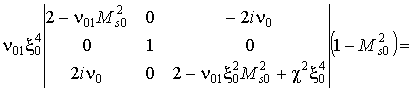
![]()
Последнее уравнение можно представить в форме
![]() (4)
(4)
где
![]()
![]()
Для x ≠ 0 уравнение (4) превращается в тождество, если один
из сомножителей (f или f3) равен
нулю.
При f3(c3) = 0, находим c3 = cs0 = (µ0/r0)1/2, где cs0 –
скорость распространения поперечных волн. Так как c3 не
зависит от x, то все гармонические
волны данной поляризации распространяются с одной и той же скоростью cs0 и явление дисперсии
(расплывание профиля негармонической волны) отсутствует.
Предположим, что цилиндрическую оболочку можно
рассматривать как упругий стержень для продольных гармонических волн лишь в
случае, когда геометрические размеры сечения оболочки малы по сравнению с
длиной волны, и поэтому параметры сечения можно усреднить. Такое предположение
выполняется при x ® 0. Тогда в сомножителе f(c1, c2) можно положить x = 0.
В этом случае, имеем
![]()
откуда находим значение функции c1 = c(0)1(x(0)1) при x ® 0
![]() –
–
скорость продольной волны в стержне.
Рассмотрим случай распространения в оболочке волн с учётом
её тонкостенности. Тогда длина волны должна быть малой, а волновое число x – большим. Приведём f к виду
![]()
Приравнивая
полученное выражение к нулю и сокращая его на ![]() , при x ® ¥ получим
, при x ® ¥ получим
![]()
откуда находим асимптоту функции c2 = c(0)2(x(0)2) при x ® ¥
![]() –
–
известную из теории пластин формулу для продольной волны
Аналогично можно показать, что при n ¹ 0 и x ® ¥ функции c2 = c(n)2(x(n)2), c3 = c(n)3(x(n)3) имеют
соответственно асимптоты c2 = c2* и c3 = c3*= cs0 = (µ0/r0)1/2.
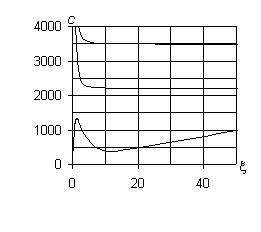
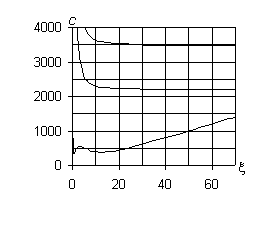
2. На рис. 1 приведены рассчитанные численно дисперсионные
диаграммы для бетонного трубопровода. Параметры трубопровода: R = 1 м, h0 = 0,02 м, n0 = 0,2,
m0 = 1,21×1010Па, r0 = 2,5×103кг/м3; скорости распространения
поперечных и продольных волн в бетоне – cs0 = 2200 м/с, cp0 = 3593 м/с.
Каждому значению n соответствуют три диаграммы, описываемые функциями ci = c(n)i(x(n)i) (i = 1,2,3).
При n = 0 на рис. 1, а показана характерная для этого случая прямая
горизонтальная линия c3 = cs0 = (µ0/r0)1/2 = 2200 м/с, выше
которой проходит кривая c2 = c(0)2(x(0)2)
имеющая асимптоты c2 = c2*= 3478,5 м/с
и x = 0. Большая
часть кривой c1 = c(0)1(x(0)1)
расположена ниже прямой c3 = 2200 м/с.
Эта кривая имеет минимум c1 = c(0)* = 370 м/с, а
также наклонную асимптоту при x ® ¥ и c1 > c(0)* (наличие
наклонной асимптоты при указанных условиях характерно для любых n). Кроме того,
c1 = c1° = (E0/r0)1/2 = 3408,2 м/с,
при x ® 0.
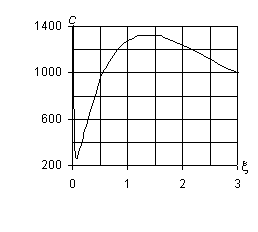
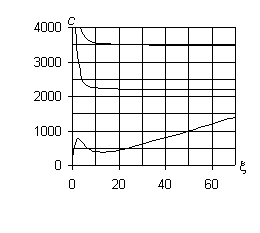
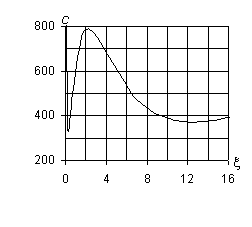
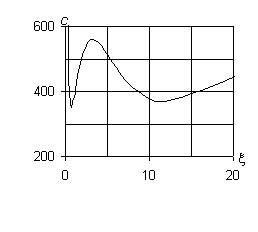
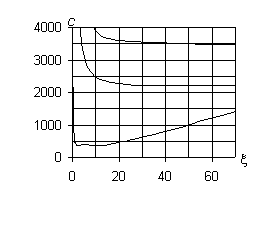
При n ¹ 0 (рис. 1, б – ж) все собственные гармонические
волны в трубопроводе являются диспергирующими. Характер изменения дисперсионных
диаграмм несколько меняется. Верхняя кривая по-прежнему имеет асимптоты c2 = c2*= 3478,5 м/с и x = 0, средняя кривая – асимптоты x = 0 и c3 = c3*= cs0 = 2200 м/с. Причём, с увеличением |n| максимальная кривизна этих диаграмм уменьшается. При небольших |n| нижняя кривая имеет три экстремума: для |n| = 1 – c¢(1)* = 262 м/с, c¢¢(1)* = 1320 м/с, c(1)* = 370 м/с; для |n| = 2 – c¢(2)* = 330 м/с, c¢¢(2)* = 792 м/с, c(2)* = 370 м/с; для |n| = 3 – c¢(3)* = 350 м/с, c¢¢(3)* = 560 м/с, c(3)* = 370 м/с; для |n| = 5 – c¢(5)* = 363 м/с, c¢¢(5)* = 390 м/с, c(5)* = 370 м/с.
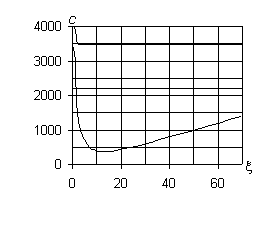
а) n = 0
б) |n| = 1
в) |n| = 2
г) |n| = 3
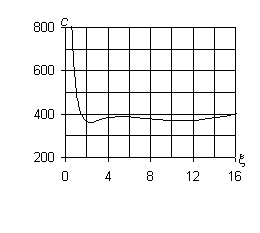
д) |n| = 5
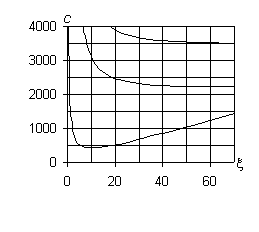
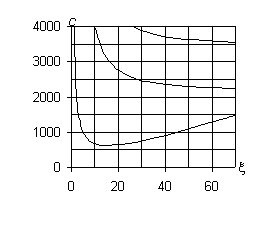
е) |n| = 10 ж) |n| = 15
Рис. 1 – Дисперсионные кривые для
бетонного трубопровода
Из анализа приведенных данных следует, что при
возрастании |n| характер поведения нижней кривой стабилизируется,
кривая принимает аналогичный для n = 0 вид с
минимальным значением c1 = c(0)* = 370 м/с. Дальнейшее увеличение |n| ведёт к возрастанию c(n)*: c(10)* = 435 м/с, c(15)* = 613 м/с, c(20)* = 808 м/с.
Как показали расчёты, при увеличении жёсткости
материала трубопровода и его толщины минимальные значения скоростей c = c(n)*
распространения свободных волн в трубопроводе возрастают.
Литература
1 Гуляев В.И., Луговой П.З., Лысюк Н.А.
Распространение гармонических волн в цилиндрической оболочке (Модель
С.П. Тимошенко) //Прикл. механика. – Киев, 2003. – Т. 39,
№ 4. – С.108-116.
2 Пожуев В.И., Львовский В.М. Реакция цилиндрической
оболочки в упругой среде на действие подвижной нагрузки //Изв. вузов. Строительство и архитектура. – 1976.
– № 2. – С. 61-66.
3 Вольмир А.С.
Нелинейная динамика пластин и оболочек. – М.: Наука, 1972. – 432 с.